• 26Set

    Aula 7

    Regressão Estatística - Parte 2

    • Regressão Linear
      ... mais um exercício para consolidação do aprendizado.

    • Considere a situação encontrada pelo gestor de duas ETAs (Estações de Tratamento de Águas):

      Em ambas as estações, a água passa pelas seis etapas regulares de tratamento:

      1) Captação, coleta inicial da água e passagem por um sistema de grades para retenção de detritos maiores. 

      2) Coagulação, adição de cal hidratada (hidróxido de cálcio) e sulfato de alumínio, para agregar as partículas de sujeira (coagulação). 

      3) Floculação, promoção da união das partículas de sujeira (flocos) em solução alcalina. Nessa etapa, o sulfato de alumínio reage com íons hidroxila para formação de polieletrólitos de alumínio (união eletrostática com partículas de argila formando elementos com microestrutura porosa - flóculos). 

      4) Decantação, a água não é mais agitada e os flocos vão se depositando no fundo, separando-se da água. O material decantado, denominado lodo, é transferido para tanques de depuração e eventual transformação em adubo em biodigestores. 

      5) Filtração. A água já decantada passa por um filtro de cascalho/areia/antracito (carvão mineral) para completa retenção dos flocos que não foram decantados na fase anterior e de alguns microrganismos. 

      6) Cloração. Etapa final do tratatmento à base de compostos clorados para eliminação de microorganismos patogênicos e como oxidante de compostos orgânicos e inorgânicos que ainda possam estar presentes.

      Médias dos apontamentos feitos pelo gestor dessas ETAs nos últimos 10 anos mostram que existe uma relação entre as quantidades consumidas de hidróxido de cálcio (H, em tons) e a precipitação média, na região de coleta do esgoto (P, em mm), nos 45 dias anteriores ao monitoramento químico do processo de coagulação.


      Os valores usados para gerar o gráfico são resumidos em uma planilha Excel (clique AQUI para fazer o download dessa planilha).  O gestor suspeita que, devido à diferente configuração dos tanques e equipamentos, o comportamento do tratamento é diferente nas duas estações.

      Estude os dados com os seus colegas e tire uma conclusão.
      Apresente as suas conclusões durante a aula.

    • Regressão Linear
      Entendendo a tabela de análise de variância, o coeficiente de correlação (r) e o coeficiente de determinação (r2)
    • T06 Tarefa

      TAREFA 06

      Transforme o intervalo de células A1..N32 da planilha LCF280_A07_Exercicio1.xlsx disponibilizada logo abaixo em um documento PDF. Nomeie o seu arquivo PDF usando o seguintge padrão:

      T06_<NoUSP>.pdf    (use o seu número USP para identificar a sua tarefa)

      Vimos na seção anterior que podemos estimar os coeficientes da equação de reta que expressa a relação linear entre duas variáveis. Aprendemos que a Tabela de Análise de Variância (ANOVA) da Regressão Linear nos ajuda a medir a variação dos dados quando ajustados pela equação de reta, ou seja, nos ajuda a conferir se o modelo proposto (linearidade da relação entre as duas variáveis) explica bem o comportamento dos dados.

      A questão é:   Quão bom é esse ajuste?   Qual o grau de explicação desse modelo linear?

      Para responder essas questões usamos os dois conceitos estatísticos apresentados na parte final do roteiro de estudos da aula passada:

      coeficiente de correlação       e       coeficiente de determinação

      Vamos praticar o uso desses dois conceitos em um novo problema. Considere a questão que alguns cientistas florestais encontraram ao perceber um certo declínio no crescimento das florestas em várias partes do mundo. Um aspecto desse declínio é o possível efeito das emissões de usinas de energia elétrica com base em carvão mineral. Nesse caso, os cientistas estão especialmente preocupados com a relação “nível de pH do solo” e “crescimento das árvores”. Estudos em várias florestas expostas a esse problema vêm sendo conduzidos, através da análise do crescimento das árvores e do pH dos solos nessas regiões. O interesse é avaliar os impactos sobre o crescimento das árvores conforme o solo se torna mais ácido. Índices de redução do crescimento são construídos para certos parâmetros florestais, onde altos valores expressam altos declínios de crescimento. Quanto maior o pH do solo, mais ácido é o solo. Vinte e três talhões próximos a usinas que utilizam o carvão mineral foram selecionadas em um determinado estudo. O índice de redução do crescimento e o correspondente pH médio do solo observados nesses estudos foram plotados no seguinte gráfico.


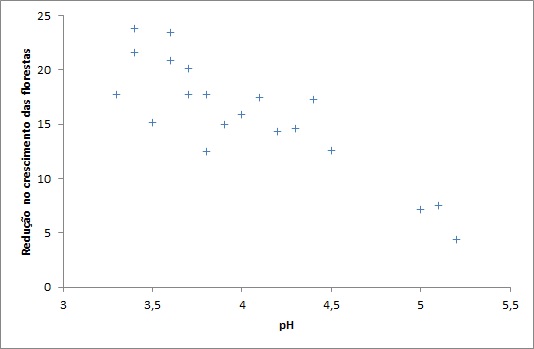
      Usaremos a análise estatística dos dados que geraram esse gráfico para tirar algumas conclusões? Faça o download da planilha de dados clicando aqui, e complete os cálculos necessários para a obtenção dos coeficientes do modelo de regressão linear, dos valores da tabela de análise de variância, e os valores dos coeficientes de correlação e de determinação. Resuma as suas conclusões com base nesses resultados.
    • Regressão Linear
      Uso de variáveis transformadas
    • T07 Tarefa

      TAREFA 07

      Transforme o intervalo de células A1..O12 da planilha LCF280_A07_Exercicio2.xlsx disponibilizada logo abaixo em um documento PDF.  Nomeie o seu arquivo PDF usando o seguintge padrão:

      T07_<NoUSP>.pdf    (use o seu número USP para identificar a sua tarefa)

      Durante a fase exploratória de dados, é comum encontrarmos uma relação aparentemente não linear entre duas variáveis. Métodos específicos para o ajuste de relações não lineares existem, mas estão fora do escopo deste curso.  Entretanto, em alguns casos, uma simples transformação matemática numa das variáveis (dependente ou independente), ou nas duas, torna a relação mais linear e viáveis os métodos de regressão estudados até agora. Vejamos o seguinte problema.

      Uma empresa que oferece serviços de asfaltamento para prefeituras observa a seguinte relação entre tamanho da equipe e área asfaltada. Essa empresa está no mercado há vários anos e utiliza técnicas convencionais de asfaltamento. Um novo composto fabricado com borracha extraída de pneus reciclados será oferecido a seus clientes. A empresa precisa de estimativas de custo de asfaltamento para esse composto e resolve analisar, com base em experiência prévia, a relação “área asfaltada” x “equipes de trabalho”. Uma análise preliminar e exploratória de 150 ordens de serviço anteriores está disponível para essa análise.


      Usaremos a análise estatística dos dados que geraram esse gráfico para tirar algumas conclusões. Continuaremos fazendo as pressuposições básicas já conhecidas:

      1. A relação entre a variável dependente y e a variável independente x é linear (y = β0 + β1 x + ε) com valor esperado do erro igual a 0, ou seja, E(εi)=0 para todo i.
      2. Todos os erros têm a mesma variância, ou seja, Var(εi) = σ2 para todo i.
      3. Os erros são independentes entre si.
      4. Os erros são normalmente distribuídos, ou seja, εi é normalmente distribuído para todo i.

      Ao observarmos o gráfico,vemos que o aumento do tamanho da equipe, apesar do aumento na área asfaltada, não é linear. De fato, a partir de um certo tamanho, o aumento da equipe parece não levar a aumentos de área asfaltada expressivos. A taxa de crescimento da área asfaltada por jornada de trabalho conforme aumentamos a equipe parece ser decrescente.

      Nesse tipo de situação, avaliaremos se a transformação das variáveis do problema pode ser recomendada dando os seguintes passos:

      1. Se a análise exploratória dos dados indica uma relação crescente a taxas decrescentes, e se a variabilidade em torno da estimativa for aproximadamente constante, transforme x usando raiz quadrada, logaritmo ou inverso.
      2. Se a análise indicar uma relação crescente a taxas crescentes, e se a variabilidade em torno da estimativa for aproximadamente constante, considere x e x2 simultaneamente como variáveis explicativas. Como este método envolve duas variáveis, utilize métodos de regressão múltipla.
      3. Se a análise indicar uma relação crescente até certo máximo com subsequente decréscimo, e se a variabilidade em torno da estimativa for aproximadamente constante, considere também o uso de x e x2 como variáveis explicativas em um único modelo de regressão linear múltipla.
      4. Se a análise indicar uma relação crescente a taxas decrescentes, e se a variabilidade em torno da estimativa também crescer com o aumento do valor y estimado, experimente o uso de y2 como variável dependente.
      5. Se a análise indicar uma relação crescente a taxas crescentes com variabilidade em torno da estimativa também crescente conforme y aumenta, experimente o uso de ln(y) como variável dependente. Pode também ser útil às vezes, considerar o logaritmo natural da variável independente, ln(x). 

       Faça o download da planilha de dados clicando aqui, aplique a transformação que você acha mais recomendada seguindo as sugestões acima. Complete os cálculos necessários para a obtenção dos coeficientes do modelo de regressão linear, dos valores da tabela de análise de variância, e os valores dos coeficientes de correlação e de determinação. Compare com os resultados oferecidos pelo Excel e resuma as suas conclusões.
◄19Set03/Out►