Programação
-
Aula 4
Explorando dados – Medidas de posição, dispersão e concentração
-
Procure no Excel as funções estatísticas que calculam as medidas de tendência central e de dispersão estudadas nos apontamentos resumidos nas primeiras seções desta página.
Considere os dados já explorados em sala de aula e que foram coletados pela empresa ECOLOG e que mostram a grande diversidade de espécies arbóreas da Amazônia (clique AQUI para download da planilha com esses dados).
Identifique as três espécies de maior ocorrência (as mais frequentes) e para cada uma delas, em uma planilha Excel, calcule as referidas medidas de tendência central e de dispersão. Organize esses resultados em um quadro, converta para PDF e submeta a sua tarefa seguindo as seguintes instruções.
Tarefa (T02)
A sua tarefa deve ser entregue no formato PDF, clicando no link disponível na primeira linha desta seção.
Tarefas entregues em outros formatos (doc, xlx, ppt etc.) serão desconsideradas.
Nomeie o seu arquivo PDF usando o seguinte padrão:
T02_<NoUSP>.pdf (use o seu número USP para identificar a sua tarefa)
-
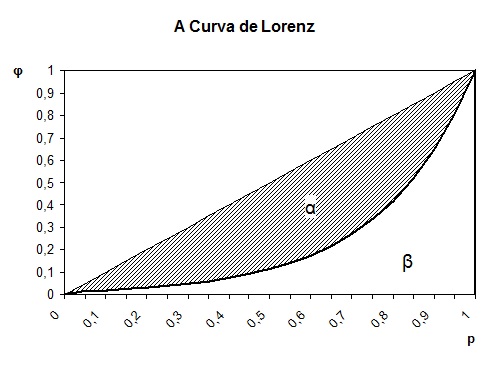
Este questionário tem apenas uma questão e trata de um único conceito, o índice de Gini.
A questão testa a sua compreensão sobre o significado desse índice.