Livro Equações de Maxwell
Equações de Maxwell. Origens, interpretações e base matemática.
3. Campo Magnético
3.2. Cargas elétricas em movimento
Esta seção é uma tradução livre da Seção 5.9 do Purcell-Morin.
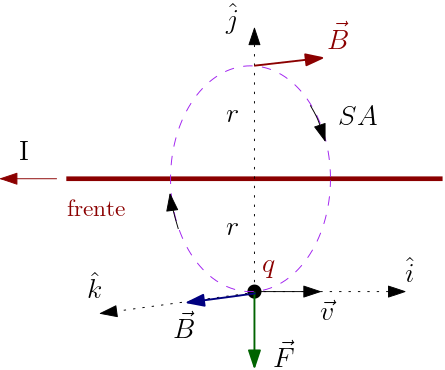
Considere a Figura 1, onde temos uma carga elétrica teste \(q\) com velocidade $\vec{v}$ a uma distância $y=r$ de um fio infinito com uma corrente elétrica $I$. Despreza a espessura do fio infinito, tudo em relação ao referencial inercial $\mathcal{O}$. O referencial inercial $\mathcal{O}$ é solidário ao fio. O referencial inercial $\mathcal{O}'$ é solidário (instantaneamente) à carga elétrica teste e o referencial inercial $\mathcal{O}''$ é solidário aos elétrons (pontos azuis) na corrente elétrica. Note que a corrente elétrica é no sentido inverso da velocidade dos elétrons, devido à carga elétrica negativa dos elétrons.
A densidade linear de cargas elétricas positivas (íons, fixos, pontos vermelhos) no fio é $\lambda_{0}$. Sendo o fio um condutor neutro, a densidade de cargas elétricas negativas (elétrons, pontos azuis) é $-\lambda_{0}$. Portanto, no referencial inercial $\mathcal{O}$, solidário ao fio, não há campo elétrico ($\vec{E}$) na região externa ao fio, como podemos concluir aplicando a lei de Gauss (a carga interna à superfície gaussiana, um cilindro de raio $r$, é nula). Isto significa que se a carga elétrica teste estiver em repouso, ela não sentirá qualquer força. Mas o que acontecerá com a carga elétrica teste caso ela esteja em movimento?
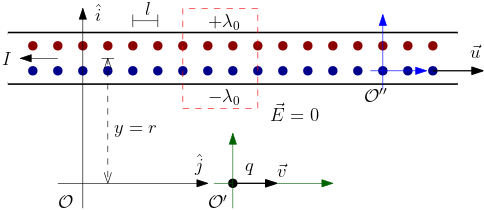
Suponha que a carga teste $q$ esteja se movimentando em relação ao fio, com velocidade $\vec{v}$, digamos ao longo do eixo horizontal do referencial inercial $\mathcal{O}$ (solidário ao fio). No referencial $\mathcal{O}'$ (solidário à carga teste), o fio está em movimento, com velocidade $-\vec{v}$. Devido à contração espacial da Relatividade Especial, a carga teste vê a distância $l$ entre os íons um pouco menor, $l/\gamma$, onde
\begin{equation}\gamma=\frac{1}{\sqrt{1-\beta^2}}\geq 1,\; \beta=\frac{v}{c}. \end{equation}Isto significa que a densidade linear (carga por comprimento) dos íons vista no referencial da carga teste é um pouco maior, $\lambda'_{+}=\gamma\,\lambda_{0}$, que a densidade $\lambda_{0}$ vista no referencial $\mathcal{O}$. A densidade linear vista em movimento é sempre aumentada pelo fator $\gamma$. Assim, o elétron (na corrente), em seu referencial $\mathcal{O}''$, imagina que a densidade própria (no referencial $\mathcal{O}$) dos íons (agora em movimento) seja $\lambda''$, vista em movimento como $\gamma_{ei}\lambda''$. Esta densidade vista pelo elétron precisa ser $\lambda_{0}$, devido ao fio condutor ser eletricamente neutro e a densidade dos elétrons ser $-\lambda_{0}$. Portanto, a densidade dos íons que o elétron vê em seu referencial é $\lambda''=\lambda_{0}/\gamma_{ei}$, com
\begin{equation} \gamma_{ei}=\frac{1}{\sqrt{1-\beta^{2}_{ei}}},\; \beta_{ei}=\frac{u}{c}, \end{equation}onde $\vec{u}$ é a velocidade do elétron relativa aos íons. Ao mudarmos para o referencial da carga teste, temos que compor a velocidade relativa $v$ do fio com a velocidade relativa $u$ do elétron (em relação ao fio), ambas na mesma direção, para encontrar a velocidade relativa $w$ do elétron em relação à carga teste (verifique),
\begin{equation} \beta_{eq}=\frac{\beta_{ei}-\beta}{1-\beta_{ei}\beta},\; \beta_{eq}=\frac{w}{c},\; \gamma_{eq}=\frac{1}{\sqrt{1-\beta^{2}_{eq}}}= (1-\beta_{ei}\beta)\gamma_{ei}\gamma. \end{equation}Finalmente podemos obter a densidade eletrônica vista pela carga teste,
\begin{equation} \lambda'_{-}=-\lambda''\gamma_{eq}=-\lambda_{0}(1-\beta_{ei}\beta)\gamma. \end{equation}Desta vez, a densidade total vista pela carga teste não é mais nula,
\begin{equation} \lambda'=\lambda'_{-}+\lambda'_{+}=\lambda_{0}\beta_{ei}\beta\gamma. \end{equation}Desta forma, a carga teste em movimento sente a presença de um campo elétrico (de um fio infinito com densidade linear $\lambda'$) e, consequentemente, uma força,
\begin{equation} E'(r)=-2C_{e}\frac{\lambda'}{r},\; F'(r)=qE'(r)= -2C_{e}\frac{q\lambda_{0}\beta_{ei}\beta}{r}\gamma. \end{equation}Os referenciais inerciais $\mathcal{O}$ e $\mathcal{O}'$ estão alinhados de forma a termos $y'=y$ (ou $r'=r$). Note que esta força é perpendicular à direção do movimento e dependente da velocidade. Esta força é vista no referencial $\mathcal{O}$ (solidário ao fio) com uma intensidade diminuída,
\begin{equation} F(r)=\frac{F'(r)}{\gamma}= -2C_{e}\frac{q\lambda_{0}\beta_{ei}\beta}{r}= 2\frac{C_{e}}{c^2}q\frac{vI}{r}= 2C_{m}q\frac{vI}{r}, \end{equation}onde introduzimos a corrente elétrica $I=-\lambda_{0}u=-\lambda_{0}\beta_{ei}c$ e a constante magnética via velocidade da luz, $c^2=C_{e}/C_{m}$. Esta força está no sentido negativo do eixo vertical ($I<0$), o qual é perpendicular à direção do movimento da carga teste. Este resultado pode ser reescrito numa forma vetorial,
\begin{equation} \vec{F}=q\,\vec{v}\times\vec{B},\; \vec{v}=v\hat{i},\; \vec{B}=-2C_{m}\frac{I}{r}\hat{k}, \end{equation}onde introduzimos o vetor $\vec{B}$, o qual é campo magnético produzido pela corrente $I$ (como veremos mais adiante). Esta é a força de Lorentz. Esse exercício mostra como uma carga elétrica em movimento produz uma força, dependente da velocidade, noutra carga elétrica também em movimento. Este resultado surpreendente resulta tomando a Relatividade Especial como correta. Veremos mais adiante que este resultado tem sido confirmado experimentalmente. A Figura 2 mostra o campo magnético $\vec{B}$ criado pela corrente $I$ no fio. Este campo atua na carga teste $q$, produzindo nela a força de Lorentz $\vec{F}$ (acima).