Livro Equações de Maxwell
| Website: | Moodle USP: e-Disciplinas |
| Kurs: | Metodos Matematicos da Fisica |
| Buch: | Livro Equações de Maxwell |
| Gedruckt von: | Gast |
| Datum: | Samstag, 29. Juni 2024, 11:56 |
Beschreibung
Equações de Maxwell. Origens, interpretações e base matemática.
1. Introdução
Os fenômenos elétricos e magnéticos são governados por leis conhecidas como "Equações de Maxwell". Cada uma destas leis é uma história à parte, unificadas em definitivo por Maxwell em 1861. Embora os efeitos elétricos, originários da existência de cargas elétricas, sejam aparentemente diferentes dos efeitos magnéticos, originários do movimento de cargas elétricas (e propriedades intrínsecas do mundo subatômico, quântico) foram unificados pelas equações de Maxwell. Um resultado notável desta unificação foi a revelação da luz como um fenômeno eletromagnético (e quântico). Outra característica surpreendente das equações de Maxwell é a íntima relação com a Relatividade Especial, estabelecida por Einstein em 1905. É nossa intenção expor aqui as equações de Maxwell, suas interpretações e relação com a Relatividade Especial, destacando as bases matemáticas.
Fatos:- Existe carga elétrica, mas não existe carga magnética.
- A carga elétrica é quantizada, isto é, existe apenas como múltiplo inteiro da carga do elétron.
- Carga elétrica é conservada e existem dois tipos (positiva e negativa).
- A velocidade da luz é uma constante universal.
- Coulomb (1785): \(\displaystyle\vec{\nabla}\cdot\vec{E}=4\pi C_{e}\,\rho,\; C_{e}=1/4\pi\epsilon_{0}\).
- Ausência de carga magnética (1861): \(\displaystyle\vec{\nabla}\cdot\vec{B}=0\).
- Ampère (1820): \(\displaystyle\vec{\nabla}\times\vec{B}= +\frac{1}{c^2}\frac{\partial\vec{E}}{\partial t} + 4\pi C_{m}\vec{J},\; C_{m}=\mu_{0}/4\pi\).
- Faraday (1821): \(\displaystyle\vec{\nabla}\times\vec{E}= -\frac{\partial\vec{B}}{\partial t}\).
Quem é quem: Velocidade da luz: \(c^{2}=C_{e}/C_{m}=1/\epsilon_{0}\mu_{0}\), onde \(\epsilon_{0}\) é a constante elétrica (ou permissividade do vácuo) e \(\mu_{0}\) é a constante magnética
(ou permeabilidade do vácuo). \(q\) é uma carga teste, \(\rho\) é a densidade de carga (por unidade de volume) da fonte e \(\vec{J}\) é a densidade de corrente (por unidade de área), a qual será definida mais adiante. A unidade de carga elétrica foi
denominada de Coulomb (C). Carga elétrica em movimento é corrente elétrica, carga por unidade de tempo, cuja unidade é Ampere (A=C/s). Os vetores \(\vec{E}\) e \(\vec{B}\) são campos vetoriais, denominados de campo elétrico e campo magnético, respectivamente.
Esses campos vetoriais são determinados por suas fontes, distribuições de cargas elétricas e correntes elétricas, de forma a satisfazerem as equações de Maxwell. Campos são funções conhecidas da posição e do tempo. Portanto, as equações de Maxwell estabelecem
vínculos entres as taxas de variação (no espaço-tempo) das componentes dos campos vetoriais elétrico e magnético. Esses vínculos são equações diferenciais parciais (EDP) lineares. Como consequência, apenas duas entre as seis componentes destes campos
vetoriais \(\vec{E}\) e \(\vec{B}\) serão independentes.
| Coulomb (1785) | Sem carga magnética (1861) | Ampère (1820)
|
Faraday (1821) |
|---|---|---|---|
| $\displaystyle\vec{\nabla}\cdot\vec{E}=4\pi C_{e}\,\rho$ | $\displaystyle\vec{\nabla}\cdot \vec{B}=0$ | $\displaystyle\vec{\nabla}\times\vec{B}= +\frac{1}{c^2}\frac{\partial\vec{E}}{\partial t} + 4\pi C_{m}\vec{J}$
|
$\displaystyle\vec{\nabla}\times\vec{E}= -\frac{\partial\vec{B}}{\partial t}$
|
| permissividade
|
permeabilidade
|
\(\displaystyle c^2=\frac{C_{e}}{C_{m}}=\frac{1}{\epsilon_{0}\mu_{0}}\)
|
carga elétrica
|
|---|---|---|---|
| \(\epsilon_{0}=8,854\, 187\, 817\, 10^{-12}\; \frac{C^{2}}{N\,m^{2}}\)
|
\(\mu_{0}=1,256\, 637\, 062\, 10^{-6}\; \frac{N\, s^{2}}{C^{2}}\)
|
\(c=299\, 792\, 458,0\; \frac{m}{s}\)
|
\(e=1,602\, 176\, 634\, 10^{-19}\; C\)
|
2. Campo Elétrico
O campo elétrico será apresentado como originário na existência de cargas elétricas, cuja ação é definida pela força elétrica, descoberta por Coulomb em 1785. Este campo elétrico possui várias propriedades especiais devidas à sua simetria esférica e dependência
com a posição, evidenciadas por Gauss, as quais levam a uma das equações de Maxwell. Do ponto de vista matemático, o campo elétrico e a força elétrica são exemplos de campos vetoriais. Um campo vetorial é uma regra (função) para "pregarmos" vetores (flechas)
numa determinada posição espacial. Estes campos vetoriais são derivados (via gradiente) de campos escalares (potencial e energia potencial). Por sua vez, um campo escalar é uma regra (função) para "pregarmos" escalares (números) numa determinada posição
espacial. A Tabela 1 (abaixo) ilustra as inter-relações entre estes campos, discutidas um pouco mais nas subseções seguintes.
| Campo elétrico | \(\vec{E}=-\vec{\nabla}\phi\) | Potencial escalar | \(\phi=-\int\vec{E}\cdot d\vec{r}\) |
|---|---|---|---|
| Força elétrica | \(\vec{F}=q\vec{E}\) | Energia potencial | \(U=q\phi\) |
2.1. Definição
O campo elétrico \(\vec{E}\) é responsável pela força elétrica entre cargas elétricas, descoberta por Coulomb em 1785. Postula-se hoje a existência de cargas elétricas, de dois tipos (positiva e negativa), com valores (absolutos) sempre como múltiplos
inteiros da carga eletrônica (em módulo), e conservadas. Estas cargas elétricas estão presentes em elétrons e prótons, constituintes de átomos (juntamente com nêutrons, que não possuem cargas elétricas). Por razões históricas, o próton tem carga positiva
e o elétron tem carga negativa. Ambos, próton e elétron, têm a mesma intensidade da carga (\(e=1,602\, 10^{-19}\; C\)). Dado a carga fonte (pontual, por simplicidade) \(Q\), esta cria um campo vetorial
\(\displaystyle\vec{E}=C_{e}\frac{Q}{r^2}\hat{r},\; C_{e}=\frac{1}{4\pi\epsilon_{0}},\; \epsilon_{0}=8,854\times 10^{-12}\; \frac{\text{C}^{2}}{\text{N}\text{m}^{2}}\;\text{(SI)}\),
denominado de "campo elétrico". Note que estamos usando coordenadas esféricas, devido à simetria esférica deste campo vetorial: ele é sempre radial e seu módulo é o mesmo sobre a casca esférica de raio \(r\). Este campo produz uma força (newtoniana) na carga teste \(q\),
\(\vec{F}=q\vec{E}\).
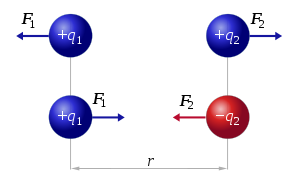
Esta é a força elétrica, foi descoberta por Coulomb em 1785. A força elétrica é a resposta à pergunta: o que faz um campo elétrico? Ele cria uma força (mensurável) numa carga teste. Os campos elétrico e gravitacional são muito semelhantes, assim como as forças elétrica e gravitacional. Uma diferença é a não existência de dois tipos de cargas gravitacional (somente positiva). A maior diferença é a não existência de cargas gravitacionais. A força gravitacional é uma consequência da curvatura do espaço-tempo, como mostrou Einstein em sua teoria da Relatividade Geral. A Figura ao lado ilustra a interação coulombiana entre duas cagas pontuais.
Dimensões e unidades. As dimensões de campo elétrico são as mesmas de força por carga,
\(\displaystyle [E]=[F/q]=\frac{ML^{2}}{QT^{2}},\quad \text{(SI):}\; \frac{N}{C}\equiv\frac{V}{m}\).
Consequentemente, as unidades de campo elétrico no sistema internacional (SI) são as mesmas unidade de força (Newton) por distância (metro), rebatizadas de Volt por metro, como mostrado acima. O Volt é uma homenagem a Alessandro Volta (1799), inventor
das modernas baterias elétricas.
Como calcular o campo elétrico produzido por uma distribuição de cargas? Havendo várias cargas fontes, \(Q_{i}\), \(i\leq N\), o campo elétrico resultante será a soma vetorial de cada campo elétrico individual,
\(\displaystyle\vec{E}=\sum_{i=1}^{N}\vec{E}_{i}= C_{e}\sum_{i=1}^{N}\frac{Q_{i}}{r_{i}^2}\hat{r}_{i}\).
Isto é possível porque a carga fonte entra de forma linear na definição do campo elétrico (dada acima). Ao invés de cargas pontuais como fontes, poderemos ter uma distribuição de cargas comm uma carga total \(Q\). O primeiro passo é admitir que esta distribuição de cargas seja contínua, mesmo sabendo que cargas elétricas existem somente como múltiplos da carga eletrônica. Esta distribuição precisa ser especificada pela sua densidade \(\rho=\rho(x,y,z,t)\) (carga por unidade de volume), um campo escalar,
\(\displaystyle Q=\int \rho dq,\; \rho=\frac{dq}{dV}\),
onde \(dq\) é o elemento de carga que ocupa o elemento de volume \(dV\). Assim, com base na definição, o campo elétrico resultante é
\(\displaystyle \vec{E}=C_{e}\int\limits_{V} \frac{\rho(\vec{r}')dV´}{r'^{2}}\hat{r}'\).
A integral é feita apenas na região contendo cargas. Por mais interessante que seja este exercício de integração múltipla, usaremos uma outra forma, bem mais simples (devida à Gauss), de calcular o campo elétrico de uma distribuição de cargas. A restrição
é que tais distribuições precisam apresentar formas simétricas.
Exercício 1. Calcule a intensidade (módulo) do campo elétrico produzido por um próton a uma distância de 0.5 Å (um Angstrom Å equivale a \(10^{-10}\) m). Resposta: \(5.759\,10^{11}\) V/m.
Exercício 2. Calcule a intensidade (módulo) da força elétrica entre um próton e um elétron separados por 0.5 Å. Resposta: \(9.226\,10^{-8}\) N.
2.2. Potencial escalar
Uma característica importante deste campo elétrico é ser conservativo. Por definição, um campo conservativo tem sua integral de caminho nula num caminho fechado \(C\),
\(\displaystyle \oint\limits_{C} \vec{E}\cdot d\vec{r}=0\).
Há várias formas de demonstrar este resultado, todas tendo a simetria esférica (ou radial) do campo elétrico como base. Essencialmente, a projeção do campo elétrico ao longo do caminho escolhido sempre terá elementos de sinais opostos, na ida e na volta,
num caminho fechado. Se convença disso fazendo alguns esboços no plano. Consequentemente, a força elétrica também será conservativa. A integral de caminho da força é o trabalho mecânico (troca de energia). Uma força conservativa leva à conservação da
energia mecânica, um escalar que se mantém constante durante o movimento.
Do ponto de vista matemático, a condição de campo conservativo leva imediatamente à existência de um campo escalar \(\phi\) cujo gradiente é proporcional a este campo,
\(\displaystyle \vec{E}=-\vec{\nabla}\phi\).
Este campo escalar é denominado, por razões históricas, de "potencial escalar". Note que, do cálculo de várias variáveis, a diferencial do potencial escalar é \(d\phi=\vec{\nabla}\phi\cdot d\vec{r}\). Substituindo esta diferencial na condição de campo conservativo, teremos
\(\displaystyle \oint\limits_{C} \vec{E}\cdot d\vec{r}= -\oint\limits_{C}\vec{\nabla}\phi\cdot d\vec{r}= -\oint\limits_{C} d\phi=0\).
A última igualdade (igual a zero) é consequência do ponto inicial da curva fechada \(C\) ser idêntico ao ponto final. Portanto, todo campo vetorial conservativo é "derivado" (via gradiente) de um campo escalar e vice-versa. O sinal negativo na frente do gradiente na introdução do potencial escalar é por mera conveniência.
Unidades e dimensões. As dimensões de potencial elétrico são as mesmas de campo elétrico vezes comprimento,
\(\displaystyle [\phi]=[\vec{E}\cdot d\vec{r}]=\frac{ML^{3}}{QT^{2}},\quad \text{(SI):}\; \frac{Nm}{C}=\frac{J}{C}=V\).
Consequentemente, as unidades de potencial elétrico no sistema internacional (SI) são as mesmas de energia (Joule) por carga, rebatizada de Volt (V) em homenagem a Alessandro Volta (1799), inventor
das baterias modernas. O Volt tem um papel fundamental nas aplicações tecnológicas (eletrônica) do eletromagnetismo.
Considerando o campo elétrico criado por uma carga pontual, o potencial escalar associado é imediato,
\(\displaystyle \phi(r)=C_{e}\frac{Q}{r}\).
Basta escrever o gradiente em coordenadas esféricas e lembrar que o potencial escalar de uma carga pontual depende apenas da distância radial. A extensão para uma distribuição de cargas se faz da forma feita para o campo elétrico. Novamente, por mais interessante que seja este exercício de calcular o potencial escalar diretamente por integração múltipla, obteremos o potencial escalar integrando (de forma indefinida) o campo elétrico,
\(\displaystyle \phi=-\int \vec{E}\cdot d\vec{r}\).
Desta forma, o potencial escalar estará definida a menos de uma constante arbitrária, a qual poderá ser escolhida por conveniência, por exemplo escolhendo o valor do potencial numa determinada posição. Aplicando este procedimento para o caso de uma carga
pontual, a expressão acima para o potencial escalar desta carga pontual teve sua constante arbitrária escolhida com o valor zero em \(r\to\infty\).
Exercício 1. Mostre que a diferencial do campo escalar \(\phi=\phi(x,y,z)\) é a projeção de seu gradiente na direção do deslocamento infinitesimal \(d\vec{r}=dx\,\hat{i}+dy\,\hat{j}+dz\,\hat{k}\) (num sistema ortonormal cartesiano de coordenadas). Sugestões: use a definição de diferencial,
\(\displaystyle d\phi=\frac{\partial\phi}{\partial x}dx+ \frac{\partial\phi}{\partial y}dy+ \frac{\partial\phi}{\partial z}dz\),
e reescreva-o em termos de um produto escalar. Use o gradiente em coordenadas cartesianas (veja o apêndice sobre o gradiente).
Exercício 2. Calcule o potencial elétrico produzido por um próton a uma distância de 0.5 Å (um Angstrom Å equivale a \(10^{-10}\) m). Resposta: \(28.797\) V.
Exercício 3. Verifique que o potencial de uma carga pontual é de fato dado pela integral indefinida de seu campo elétrico,
\(\displaystyle \phi=-\int \vec{E}\cdot d\vec{r},\quad \vec{E}=C_{e}\frac{Q}{r^2}\hat{r}\),
escolhendo a constante de integração de forma a zerar o potencial numa região muito distante (\(r\to\infty\)).
2.3. Energia potencial
Como a força elétrica numa carga teste \(q\) é dada pelo campo elétrico criado pela fonte, \(\vec{F}=q\vec{E}\), é conservativa, então podemos definir a "energia potencial" como um campo escalar dado pelo potencial,
\(\displaystyle U=q\phi,\; \vec{F}=-\vec{\nabla}U\).
Estes conceitos de energia potencial e potencial elétrico são muito importantes em eletromagnetismo, principalmente do ponto de vista técnico. Naturalmente, podemos usar a mesma prescrição para calcular o potencial elétrico via campo elétrico para calcular a energia potencial via a força elétrica, a menos de uma constante arbitrária,
\(\displaystyle U=-\int \vec{F}\cdot d\vec{r}\).
Para cargas pontuais, considerando a constante arbitrária igual a zero em regiões muito distantes, a energia potencial é (verifique)
\(\displaystyle U(r)=C_{e}\frac{qQ}{r}\).
Dimensões e unidades. As dimensões de energia potencial são as mesmas de potencial elétrico vezes carga, ou de força vezes distância (energia),
\(\displaystyle [U]=[q\phi]=\frac{ML^{3}}{T^{2}},\quad \text{(SI):}\; Nm=J\).
O Joule (J) como unidade de energia é uma homenagem a James Joule pelos seus experimentos mostrando a equivalência entre energia térmica (calor) e energia mecânica em 1843.
Exercício 1.
Calcule a energia potencial entre um próton e um elétron separados por 0.5 Å. Use Å=\(10^{-10}\) m. Resposta: \(-4.613\,10^{-18}\) J.
2.4. Lei de Gauss
Os trabalhos de Gauss em 1813 sobre Geometria deu uma excelente contribuição ao eletromagnetismo sintetizado pelas equações de Maxwell de 1861. A essência desta contribuição de Gauss, conhecida por "lei de Gauss", é a relação entre o fluxo do campo elétrico com suas cargas fonte, válida somente para campos com uma dependência com o inverso do quadrado (exatamente) da distância.
Fluxo. Um campo vetorial como o campo elétrico pode ser visualizado pelas suas linhas de campo, as quais são formadas ligando os pontos onde os vetores prescritos pelo campo vetorial são
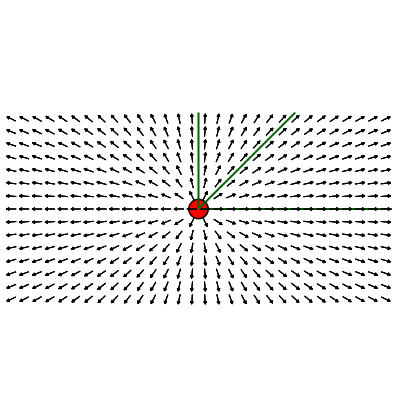
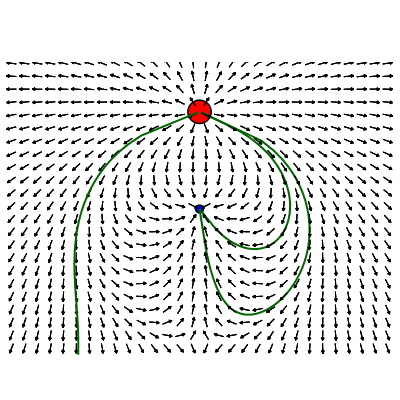
colocados de forma a serem tangentes a estas curvas. As figuras nas duas primeiras colunas da Tabela 1 ilustram as linhas de campo (no plano) para uma carga (positiva) e para duas cargas, uma positiva (vermelha) e uma negativa (azul), com carga positiva
sendo três vezes mais intensa, respectivamente. As linhas de campo são indicadas pelas curvas verdes. Note que, por definição, as linhas de campo iniciam nas cargas positivas e terminam nas cargas negativas. Agora é só extrapolar para três dimensões.
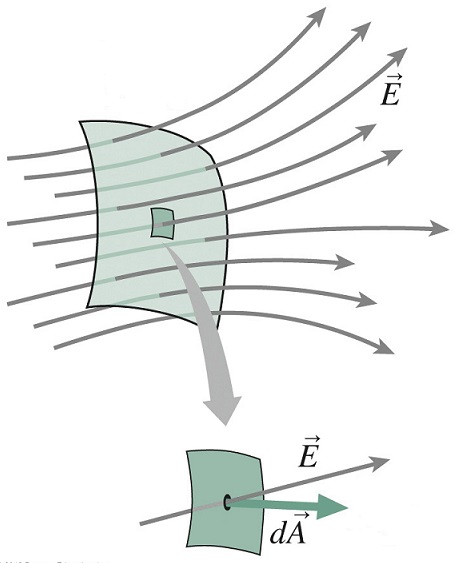
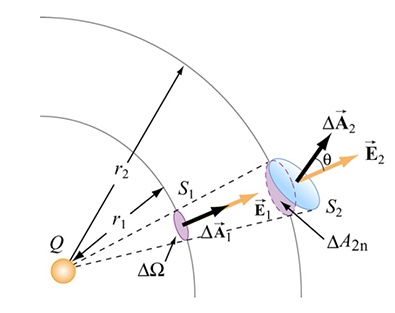
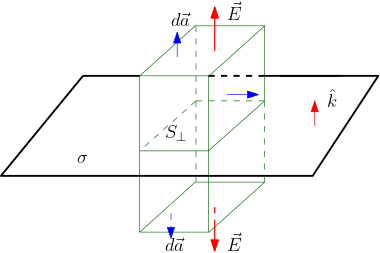
O fluxo pode ser visualizado como um número que quantifica as linhas de campo que atravessam uma determinada superfície, como mostrado na penúltima coluna da tabela acima. O fluxo é definido como
\begin{equation} \Phi=\int\limits_{A}\vec{E}\cdot d\vec{a}, \end{equation}onde o vetor elemento de área \(d\vec{a}\) (ou \(d\vec{A}\) em algumas figuras) tem intensidade \(dA\) (elemento área) na direção perpendicular ao elemento área. A integral é feita numa área finita $A$.
Ângulo sólido. A figura na última coluna da tabela acima mostra o chamado ângulo sólido (\(d\Omega\)), definido como
\begin{equation} d\Omega=\frac{\hat{r}\cdot d\vec{a}}{r^{2}},\quad\int\limits_{A}d\Omega=4\pi. \end{equation}Note o ângulo sólido é a generalização tridimensional do ângulo polar no plano, o qual é \(2\pi\) para uma curva fechada (uma volta completa) em torno da origem, não importando o formato da curva. Similarmente, o ângulo sólido é \(4\pi\) para uma superfície fechada em torno da origem, não importando o formato da curva.
| Uma carga positiva
|
Uma carga positiva e uma negativa
|
Fluxo | Ângulo sólido
|
|---|---|---|---|
|
|
|
|
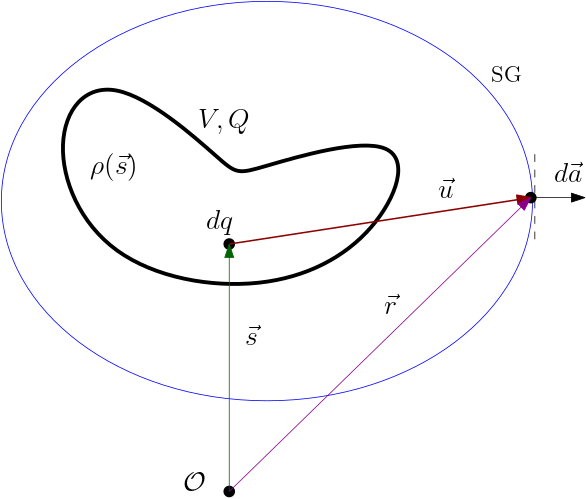
Lema de Gauss. Com estas noções de fluxo e ângulo sólido, podemos estabelecer uma relação entre as cargas fontes do campo elétrico e o seu fluxo através de uma superfície fechada contendo estas
cargas. Para tal, observe a primeira figura na Tabela 2 abaixo. Ela mostra uma carga total \(Q\) distribuída num volume \(V\) segundo a densidade \(\rho(\vec{s})\), onde o vetor posição \(\vec{s}\) localiza um elemento de carga \(dq=\rho(\vec{s})dV\)
em relação ao referencial inercial (fixo) \(\mathcal{O}\). Imagine uma superfície fechada (de área total \(A\)) envolvendo esta distribuição de cargas. Esta é denominada de superfície gaussiana (SG). Imagine também um elemento de área \(d\vec{a}\) nesta
superfície gaussiana, localizado pelo vetor posição \(\vec{r}\) em relação ao mesmo referencial inercial \(\mathcal{O}\). Esse elemento de área compreende o ângulo sólido
\begin{equation} d\Omega=\frac{\hat{u}\cdot d\vec{a}}{u^{2}}, \end{equation}
onde \(\vec{u}=\vec{r}-\vec{s}\). Note que o ângulo sólido compreendido pela superfície gaussiana SG é sempre \(4\pi\), independentemente da posição do elemento de carga \(dq\), desde que SG contenha a distribuição de cargas completamente. O ângulo sólido não depende da origem do sistema de coordenadas utilizado. Calculemos agora o fluxo (através da superfície gaussiana SG) do campo elétrico produzido por esta distribuição de cargas,
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}, \end{equation}
onde o campo elétrico na posição \(\vec{r}\) é a soma de todas as contribuições dos elementos de carga \(dq\) dentro da distribuição,
\begin{equation} \vec{E}(\vec{r})=C_{e}\int\limits_{Q}dq\frac{\vec{u}}{u^{2}}=C_{e}\int\limits_{V}dV\rho(\vec{s})\frac{\hat{u}}{u^{2}},\; \vec{u}=\vec{r}-\vec{s},\; dq=\rho(\vec{s}) dV. \end{equation}
Substituindo esta expressão no fluxo,
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}=C_{e}\int\limits_{V}dV\rho(\vec{s})\oint\limits_{A}\frac{\hat{u}\cdot d\vec{a}}{u^{2}}=C_{e}\int\limits_{V}dV\rho(\vec{s})\oint\limits_{A}d\Omega=4\pi C_{e}\int\limits_{V}dV\rho(\vec{s})=4\pi Q.\end{equation}
Magnífico! O fluxo total, através de uma superfície fechada e arbitrária, contendo uma distribuição de cargas é simplesmente proporcional à carga total desta distribuição. Esse é o Lema de Gauss. Note que se a dependência do campo vetorial com a posição
não for exatamente o inverso do quadrado, não teríamos este resultado surpreendente. Ou seja, o Lema de Gauss é uma consequência da Lei de Coulomb.
| Geral | Ponto (\(d\vec{a}=da\,\hat{r}\)) | Esfera (\(d\vec{a}=da\,\hat{r}\)) | Plano (\(d\vec{a}=\pm da\,\hat{k}\)) |
|---|---|---|---|
|
|
|
|
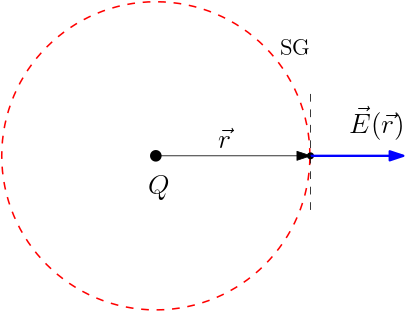
Exemplo 1. Vale manter em mente que a superfície gaussiana é arbitrária, a qual podemos escolher de acordo com nossa conveniência. Assim, podemos calcular campos elétricos de distribuições com simetria. Como exemplo, considere a segunda figura na Tabela 2, mostrando uma carga pontual \(Q\). Como o campo elétrico de uma carga pontual tem simetria esférica, ele deve ser da forma \(\vec{E}(\vec{r})=E(r)\hat{r}\) (simetria radial). Neste caso, a melhor escolha para a superfície gaussiana (SG) é uma casca esférica de raio \(r\). Esta escolha faz com que o campo elétrico seja perpendicular a esta superfície e paralelo ao vetor elemento de área \(d\vec{a}=da\,\hat{r}\) (sempre apontando para fora), em qualquer ponto. Portanto sabemos calcular seu fluxo através de SG:
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}=E(r)\oint\limits_{A}da=4\pi r^{2}E(r)=4\pi C_{e}Q\;\implies\; E(r)=C_{e}\frac{Q}{r^{2}}.\end{equation}
Certamente já sabíamos deste resultado. No entanto, podemos usar o mesmo procedimento para o campo de uma distribuição esférica, cilíndrica ou plana, para citar algumas distribuições altamente simétricas.
3. Campo Magnético
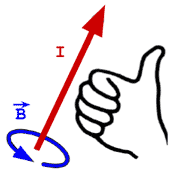
Definição. Como o campo elétrico \(\vec{E}\), o campo magnético \(\vec{B}\) pode ser definido pela sua ação em uma carga teste \(q\),
\begin{equation} \vec{F}=q\,\vec{v}\times\vec{B}\end{equation}conhecida como força de Lorentz (1895), mas identificada por Maxwell em 1861. Esta força magnética apresenta duas características inexistentes na força elétrica \(\vec{F}=q\vec{E}\): (i) ela
é um pseudo-vetor (devido ao produto vetorial) e (ii) ela é dependente da velocidade da carga teste. Um pseudo-vetor, resultante de um produto vetorial, não inverte seu sentido quando o sentido de cada vetor no produto vetorial é invertido. Da mesma
forma, o número resultante de um produto escalar é um pseudo-escalar. Os produtos escalar e vetorial são operações binárias entre vetores.
Ausência de carga magnética. Diferentemente do campo elétrico, o qual é oriundo de uma carga elétrica fonte, nunca se observou a existência de uma carga magnética fonte. Desta forma, temos a segunda equação de Maxwell,
\begin{equation} \vec{\nabla}\cdot\vec{B}=0,\end{equation}pois o divergente indica a presença de uma carga fonte, como aprendemos aplicando o teorema de Gauss à lei de Coulomb. Como cargas magnéticas "não existem", o divergente do campo magnético deve ser nulo.
Dimensões. As dimensões do campo magnético \(\vec{B}\) são
\begin{equation} [\vec{B}]=\biggl[\frac{||\vec{F}||}{q||\vec{v}||}\biggr] = \frac{\text{M}}{\text{QT}}. \end{equation}No sistema internacional de unidades temos kg/C/s=T (Tesla) como unidades para o campo magnético.
3.1. Carga magnética
Campo. Suponha que, além da carga elétrica \(Q_{e}\), exista também a carga magnética $Q_{m}$, como fonte de um campo magnético obedecendo a lei de Coulomb (no vazio),
\begin{equation} \vec{B}=C_{m}\frac{Q_{m}}{r^{2}}\hat{r}=C_{m}Q_{m}\frac{\vec{r}}{r^{3}} = -C_{m}Q_{m}\vec{\nabla}\frac{1}{r},\; r\neq 0, \end{equation}onde $C_{m}=\mu_{0}/4\pi$ é a constante magnética, tal que $C_{e}/C_{m}=1/\mu_{0}\epsilon_{0}=c^2$, sendo $C_{e}=1/4\pi\epsilon_{0}$ a constante elétrica e $c$ a velocidade da luz no vácuo ($\epsilon_{0}$ é a permissividade e $\mu_{0}$ é a permeabilidade do vácuo). Como no caso elétrico, o divergente do campo identifica sua fonte (neste caso, uma carga pontual),
\begin{equation} \vec{\nabla}\cdot\vec{B}= C_{m}Q_{m}\nabla^{2}\frac{1}{r}= 4\pi C_{m}\, Q_{m}\,\delta(r)=4\pi C_{m}\,\rho_{m}, \end{equation}onde usamos a distribuição delta de Dirac (3D), introduzida no Apêndice 5.3, a qual nos permite definir uma "densidade'' $\rho_{m}=Q_{m}\,\delta(r)$ para uma carga pontual $Q$.
Vale o mesmo para o campo elétrico.
Fluxo. O fluxo $\phi$ deste campo magnético produzido por uma carga pontual, com simetria radial, é calculado facilmente usando uma superfície esférica $S^{1}$ centrada na origem,
\begin{equation} \phi=\int\limits_{S^{1}} \vec{B}\cdot d\vec{a} = 4\pi C_{m}\,Q_{m},\quad d\vec{a}=dA\,\hat{r}, \end{equation}ou então usando o teorema de Gauss (veja o Apêndice 5.2),
\begin{equation} \phi=\int\limits_{S^{1}} \vec{B}\cdot d\vec{a} = \int\limits_{S^{2}} \vec{\nabla}\cdot\vec{B}\, dV = 4\pi C_{m}\,Q_{m}, \end{equation}onde $S^{2}$ é a esfera contendo a superfície esférica $S^{1}$ como borda e escrevemos o divergente do campo magnético em termos da delta de Dirac. Vale o mesmo para o campo elétrico.
Potencial. Supondo a existência desta carga magnética, quem será o potencial vetor $\vec{A}$ que dará origem ao campo magnético $\vec{B}$? Não podemos mais usar a relação $\vec{B}=\vec{\nabla}\times\vec{A}$, onde $\vec{A}$ é o potencial vetor, pois $\vec{\nabla}\cdot\vec{\nabla}\times\vec{A}=0$ fornece um fluxo nulo, sempre. Uma contradição como esta é fruto típico da "árvore" de singularidades e indica que o potencial vetor desse campo magnético deve ser irregular, singular em alguma região. Como o campo magnético possui simetria esférica (ou radial), esperamos que forma do potencial vetor deve apresentar também algum tipo de simetria, além de uma irregularidade. Dirac escolheu um potencial azimutal (simetria em torno do eixo Z),
\begin{equation} \vec{A} = A_{\phi}\,\hat{e}_{\phi}. \end{equation}Justificativas? Talvez Pauli pudesse tê-las enunciadas. Dirac não precisa delas. Com esta escolha,
\begin{align} \vec{\nabla}\times\vec{A}&= \frac{1}{r}\left(A_{\phi}\frac{\cos\theta}{\sin\theta} + \frac{\partial A_{\phi}}{\partial\theta}\right)\,\hat{e}_{r} - \left(\frac{A_{\phi}}{r} + \frac{\partial A_{\phi}}{\partial r}\right)\,\hat{e}_{\theta} \\&= -\frac{\partial A_{\phi}}{\partial z}\,\hat{e}_{\rho} + \left(\frac{A_{\phi}}{r} + \frac{\partial A_{\phi}}{\partial\rho}\right)\,\hat{e}_{k}, \end{align}em coordenadas esféricas e cilíndricas, respectivamente (verifique). Requerendo que $\vec{\nabla}\times\vec{A}=\vec{B}$, então temos duas equações diferenciais (verifique) para resolver, cuja solução geral é (verifique)
\begin{equation} A_{\phi} = C_{m}Q_{m}\frac{f(\phi)-\cos\theta}{r\sin\theta} \end{equation}para as coordenadas esféricas, e
\begin{equation} A_{\phi} = \frac{C_{m}Q_{m}}{\rho}\left( f(\phi) - \frac{z}{\sqrt{\rho^{2}+z^{2}}} \right) \end{equation}para as coordenadas cilíndricas, onde $f(\phi)$ é uma função arbitrária. Que critérios (adicionais) poderíamos usar para determinar esta função arbitrária? Se ela for $f=\pm 1$, o potencial apresenta uma irregularidade (diverge) nos semi-eixos $\rho=0$ ($r=|z|$), $z>0$ ($\theta=0$) e $z<0$ ($\theta=\pi$), respectivamente. As coordenadas cilíndricas parecem mais adequadas para percebermos tais irregularidades (verifique).
Exercício 1. Detalhe cuidadosamente cada uma das situações especificados por "verifique".
3.2. Cargas elétricas em movimento
Esta seção é uma tradução livre da Seção 5.9 do Purcell-Morin.
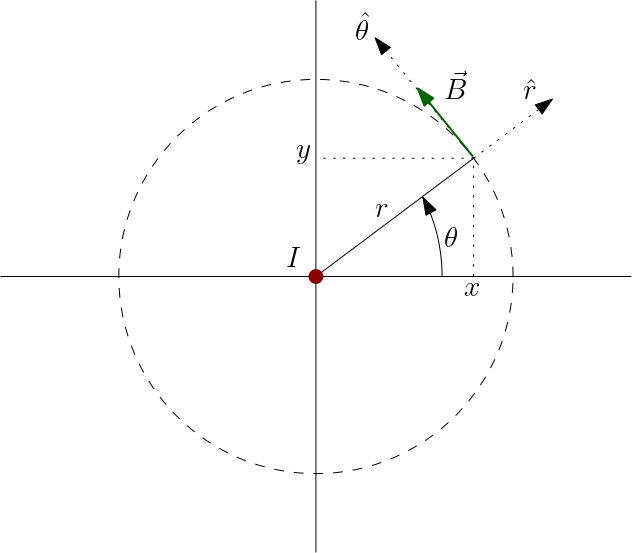
Considere a Figura 1, onde temos uma carga elétrica teste \(q\) com velocidade $\vec{v}$ a uma distância $y=r$ de um fio infinito com uma corrente elétrica $I$. Despreza a espessura do fio infinito, tudo em relação ao referencial inercial $\mathcal{O}$. O referencial inercial $\mathcal{O}$ é solidário ao fio. O referencial inercial $\mathcal{O}'$ é solidário (instantaneamente) à carga elétrica teste e o referencial inercial $\mathcal{O}''$ é solidário aos elétrons (pontos azuis) na corrente elétrica. Note que a corrente elétrica é no sentido inverso da velocidade dos elétrons, devido à carga elétrica negativa dos elétrons.
A densidade linear de cargas elétricas positivas (íons, fixos, pontos vermelhos) no fio é $\lambda_{0}$. Sendo o fio um condutor neutro, a densidade de cargas elétricas negativas (elétrons, pontos azuis) é $-\lambda_{0}$. Portanto, no referencial inercial $\mathcal{O}$, solidário ao fio, não há campo elétrico ($\vec{E}$) na região externa ao fio, como podemos concluir aplicando a lei de Gauss (a carga interna à superfície gaussiana, um cilindro de raio $r$, é nula). Isto significa que se a carga elétrica teste estiver em repouso, ela não sentirá qualquer força. Mas o que acontecerá com a carga elétrica teste caso ela esteja em movimento?
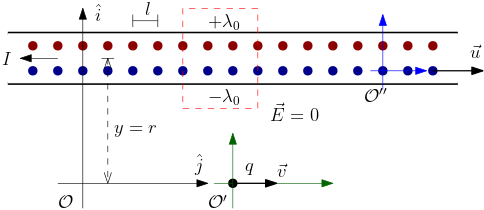
Suponha que a carga teste $q$ esteja se movimentando em relação ao fio, com velocidade $\vec{v}$, digamos ao longo do eixo horizontal do referencial inercial $\mathcal{O}$ (solidário ao fio). No referencial $\mathcal{O}'$ (solidário à carga teste), o fio está em movimento, com velocidade $-\vec{v}$. Devido à contração espacial da Relatividade Especial, a carga teste vê a distância $l$ entre os íons um pouco menor, $l/\gamma$, onde
\begin{equation}\gamma=\frac{1}{\sqrt{1-\beta^2}}\geq 1,\; \beta=\frac{v}{c}. \end{equation}Isto significa que a densidade linear (carga por comprimento) dos íons vista no referencial da carga teste é um pouco maior, $\lambda'_{+}=\gamma\,\lambda_{0}$, que a densidade $\lambda_{0}$ vista no referencial $\mathcal{O}$. A densidade linear vista em movimento é sempre aumentada pelo fator $\gamma$. Assim, o elétron (na corrente), em seu referencial $\mathcal{O}''$, imagina que a densidade própria (no referencial $\mathcal{O}$) dos íons (agora em movimento) seja $\lambda''$, vista em movimento como $\gamma_{ei}\lambda''$. Esta densidade vista pelo elétron precisa ser $\lambda_{0}$, devido ao fio condutor ser eletricamente neutro e a densidade dos elétrons ser $-\lambda_{0}$. Portanto, a densidade dos íons que o elétron vê em seu referencial é $\lambda''=\lambda_{0}/\gamma_{ei}$, com
\begin{equation} \gamma_{ei}=\frac{1}{\sqrt{1-\beta^{2}_{ei}}},\; \beta_{ei}=\frac{u}{c}, \end{equation}onde $\vec{u}$ é a velocidade do elétron relativa aos íons. Ao mudarmos para o referencial da carga teste, temos que compor a velocidade relativa $v$ do fio com a velocidade relativa $u$ do elétron (em relação ao fio), ambas na mesma direção, para encontrar a velocidade relativa $w$ do elétron em relação à carga teste (verifique),
\begin{equation} \beta_{eq}=\frac{\beta_{ei}-\beta}{1-\beta_{ei}\beta},\; \beta_{eq}=\frac{w}{c},\; \gamma_{eq}=\frac{1}{\sqrt{1-\beta^{2}_{eq}}}= (1-\beta_{ei}\beta)\gamma_{ei}\gamma. \end{equation}Finalmente podemos obter a densidade eletrônica vista pela carga teste,
\begin{equation} \lambda'_{-}=-\lambda''\gamma_{eq}=-\lambda_{0}(1-\beta_{ei}\beta)\gamma. \end{equation}Desta vez, a densidade total vista pela carga teste não é mais nula,
\begin{equation} \lambda'=\lambda'_{-}+\lambda'_{+}=\lambda_{0}\beta_{ei}\beta\gamma. \end{equation}Desta forma, a carga teste em movimento sente a presença de um campo elétrico (de um fio infinito com densidade linear $\lambda'$) e, consequentemente, uma força,
\begin{equation} E'(r)=-2C_{e}\frac{\lambda'}{r},\; F'(r)=qE'(r)= -2C_{e}\frac{q\lambda_{0}\beta_{ei}\beta}{r}\gamma. \end{equation}Os referenciais inerciais $\mathcal{O}$ e $\mathcal{O}'$ estão alinhados de forma a termos $y'=y$ (ou $r'=r$). Note que esta força é perpendicular à direção do movimento e dependente da velocidade. Esta força é vista no referencial $\mathcal{O}$ (solidário ao fio) com uma intensidade diminuída,
\begin{equation} F(r)=\frac{F'(r)}{\gamma}= -2C_{e}\frac{q\lambda_{0}\beta_{ei}\beta}{r}= 2\frac{C_{e}}{c^2}q\frac{vI}{r}= 2C_{m}q\frac{vI}{r}, \end{equation}onde introduzimos a corrente elétrica $I=-\lambda_{0}u=-\lambda_{0}\beta_{ei}c$ e a constante magnética via velocidade da luz, $c^2=C_{e}/C_{m}$. Esta força está no sentido negativo do eixo vertical ($I<0$), o qual é perpendicular à direção do movimento da carga teste. Este resultado pode ser reescrito numa forma vetorial,
\begin{equation} \vec{F}=q\,\vec{v}\times\vec{B},\; \vec{v}=v\hat{i},\; \vec{B}=-2C_{m}\frac{I}{r}\hat{k}, \end{equation}onde introduzimos o vetor $\vec{B}$, o qual é campo magnético produzido pela corrente $I$ (como veremos mais adiante). Esta é a força de Lorentz. Esse exercício mostra como uma carga elétrica em movimento produz uma força, dependente da velocidade, noutra carga elétrica também em movimento. Este resultado surpreendente resulta tomando a Relatividade Especial como correta. Veremos mais adiante que este resultado tem sido confirmado experimentalmente. A Figura 2 mostra o campo magnético $\vec{B}$ criado pela corrente $I$ no fio. Este campo atua na carga teste $q$, produzindo nela a força de Lorentz $\vec{F}$ (acima).
3.3. Densidade de Corrente
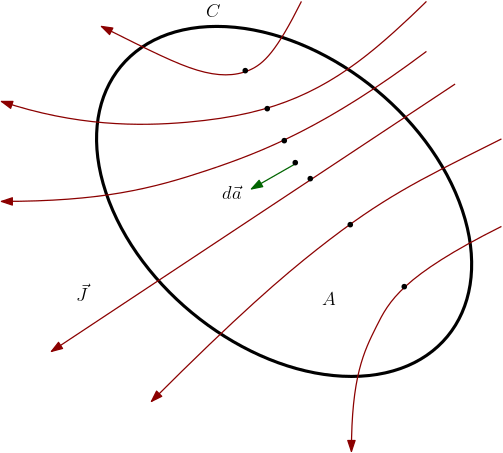
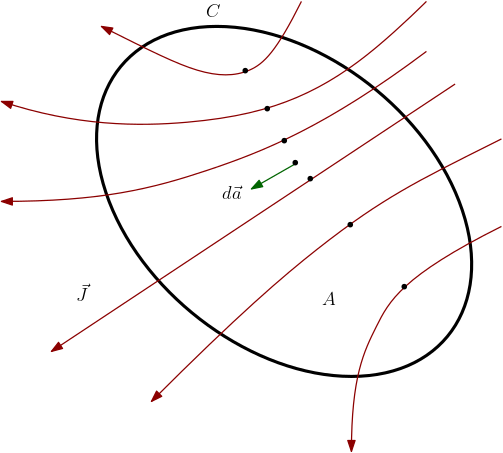
Diferentemente do campo elétrico, que é produzido por uma carga elétrica fonte, o campo magnético não tem uma carga magnética fonte. Até o momento ainda não conseguimos observar uma carga magnética, o que coloca uma grande dúvida sobre sua existência. Nossos campo magnéticos serão criados por cargas elétricas em movimento, como vimos na Seção 3.2. Portanto precisamos definir uma densidade de cargas em movimento, como um vetor. Cargas em movimento é uma corrente elétrica. Para tal, considere a Figura 1 na Tabela Densidade de Corrente. Cada portador de cargas (pontos) tem uma carga \(Q\) é uma velocidade \(\vec{u}\) (numa região muito pequena). Consideremos as cargas que atravessarão uma determinada área \(\Delta a\) num tempo \(\Delta t\). Seja \(\Delta\vec{a}\) o vetor elemento de área. O volume apoiado na área \(\Delta a\) e de altura \(u\Delta t\) é \(\Delta V=\Delta t\,\vec{u}\cdot\Delta\vec{a}\). Seja \(n\) a densidade dos portadores de cargas nesta região (a densidade de cargas é \(\rho=nQ\)). Então o total de portadores de cargas é \(n\Delta V\). Podemos definir (localmente) corrente elétrica como carga por unidade de tempo:
\begin{equation} dI=\lim\limits_{\Delta t\to 0}\frac{n\Delta V\,Q}{\Delta t}=\rho \vec{u}\cdot d\vec{a}. \end{equation}Podemos introduzir o campo vetorial densidade de corrente \(\vec{J}\) de modo a obtermos a corrente total \(I\) passando por uma área \(A\) como o fluxo (da densidade de corrente):
\begin{equation} I=\int\limits_{A} \vec{J}\cdot d\vec{a},\; \vec{J}=\rho\vec{u}. \end{equation}A unidade de de corrente elétrica no Sistema Internacional (SI) é o Ampere (A=C/s). Isto faz com que a unidade de densidade de corrente seja A/m\(^{2}\) (corrente por área).
Lei de conservação. O campo vetorial densidade de corrente \(\vec{J}\) é o campo escalar densidade de cargas estão intimamente relacionados. Para sabermos como, temos de introduzir um princípio (ou postulado): carga elétrica é conservada. Considere uma carga total \(Q\) saindo (ou entrando) de uma região de volume \(V\), na forma de uma corrente \(I=dQ/dt\). Considere uma superfície fechada, de área \(A\), contendo o volume \(V\). A carga \(dQ=\rho\,dV\) que sai desse volume \(V\) precisa atravessar a superfície \(A\) que o contém. Assim, usando a definição de corrente elétrica e princípio da conservação da carga (ou da corrente) elétrica, temos
\begin{equation} I=\oint\limits_{A} \vec{J}\cdot d\vec{a}= -\frac{dQ}{dt}= -\frac{d}{dt}\int\limits_{V}\rho\,dV. \end{equation}O sinal negativa indica que a carga está saindo da região. Podemos usar o teorema de Gauss para passar a integral de superfície para a integral de volume:
\begin{equation} \oint\limits_{A} \vec{J}\cdot d\vec{a}= \int\limits_{V}\vec{\nabla}\cdot\vec{J}\,dV=-\frac{d}{dt}\int\limits_{V}\rho\,dV\; \implies\; \vec{\nabla}\cdot\vec{J}+\frac{d\rho}{dt}=0. \end{equation}Esta última equação é conhecida por equação da continuidade.
Ela relaciona a variação temporal do campo escalar densidade de carga com a variação espacial (divergente) do campo vetorial densidade de corrente. Ela afirma (localmente) a conservação da carga: a carga que sai de uma região, sai na forma de uma corrente.

|

|
|---|---|
| Figura 1
|
Figura 2
|
3.4. Potencial vetor
A segunda equação de Maxwell tem uma solução imediata (verifique),
\begin{equation} \vec{\nabla}\cdot\vec{B}=0 \;\implies\; \vec{B}=\vec{\nabla}\times\vec{A}. \end{equation}O campo vetorial \(\vec{A}\) é conhecido como potencial vetor. Ele desempenha um papel similar ao potencial escalar \(\phi\), tal que \(\vec{E}=-\vec{\nabla}\phi\). Note que os potenciais \(\phi\) e \(\vec{A}\) dão origem aos campos vetoriais \(\vec{E}\) (elétrico) e \(\vec{B}\) (magnético), via gradiente e rotacional, respectivamente. Naturalmente, estes potenciais estão definidos a menos de uma constante arbitrária, pelo menos até o momento. Vale ressaltar que esta solução em termos de um potencial vetor, via rotacional, é válida somente na ausência de cargas magnéticas. Na presença de cargas magnéticas, o divergente do campo magnético não será nulo, em geral (veja a Seção 3.1).
Em geral, correntes são conduzidas em materiais que possuem extensões,
além de comprimentos (como num fio). Isto significa que teremos de
considerar densidades de correntes, um campo vetorial, como introduzidas
na Seção 3.3.
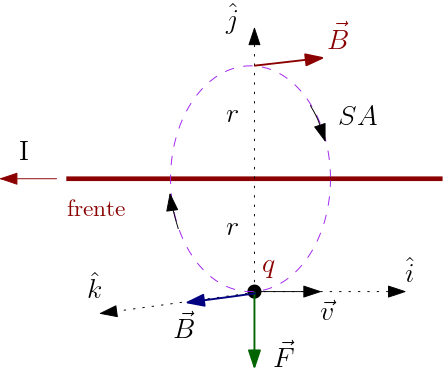
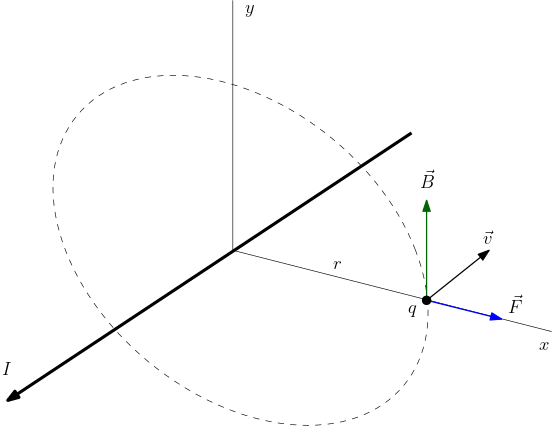
Exercício 1. Vejamos como obter o potencial vetor para o campo magnético criado por uma corrente \(I\) em um fio retilíneo. Vimos na Seção 3.2 que este campo magnético tem a forma mostrada nas Figura 1 e 2 da tabela abaixo,
\begin{equation} \vec{F}=q\,\vec{v}\times\vec{B},\; \vec{v}=-v\hat{k},\; \vec{B}=2C_{m}\frac{I}{r}\hat{\theta}.\end{equation}Queremos encontrar o potencial vetor $\vec{A}$ tal que $\vec{B}=\vec{\nabla}\times\vec{A}$. Devida à simetria cilíndrica do fio (retilíneo), melhor usar coordenadas cilíndricas, $\vec{A}=A_{r}\hat{r}+A_{\theta}\hat{\theta}+A_{z}\hat{k}$. Também devido à esta simetria, esperamos que este potencial vetor não dependa da coordenada $z$ (ao longo do fio) e nem da coordenada angular $\theta$; cada componente do potencial vetor dever ser função somente da coordenada radial $r$, $A_{r,\theta,z}=A_{r,\theta,z}(r)$. Sabemos que o campo magnético está inteiramente na direção tangencial (direção de $\hat{\theta}$). Assim,
\begin{equation} \vec{\nabla}\times\vec{A}= \left(\frac{\partial A_{r}}{\partial z}-\frac{\partial A_{z}}{\partial r}\right)\hat{\theta}= -\frac{\partial A_{z}}{\partial r}\hat{\theta}=\vec{B}= 2C_{m}\frac{I}{r}\hat{\theta}\end{equation}Desta forma,
\begin{equation} -\frac{\partial A_{z}}{\partial r}= 2C_{m}\frac{I}{r}\;\implies\; A_{z}=-2C_{m}I\ln r+cte.\end{equation}O potencial vetor está ao longo do fio, $\vec{A}=A_{z}\hat{k}$, no sentido contrário à corrente $I$. Temos ainda a liberdade de adicioná-lo qualquer campo vetorial com divergência nula.
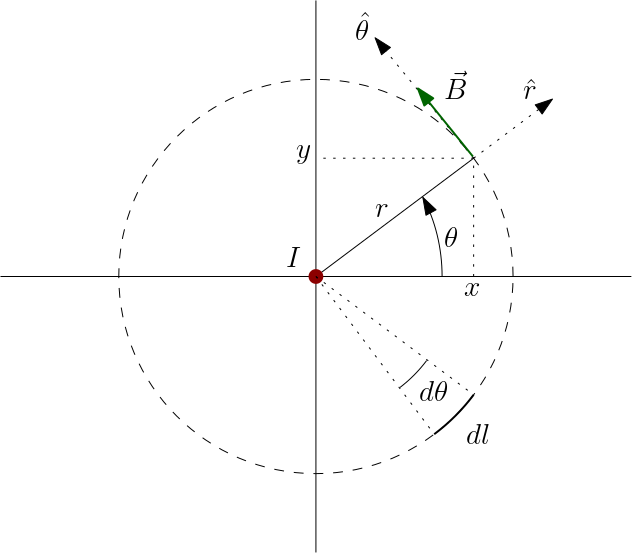
Exercício 2. Vamos mostrar que a circulação do campo magnético de uma corrente elétrica em um fio retilíneo, circulação em torno desse fio, é proporcional à corrente elétrica que ele transporta. Seja $d\vec{l}=dl\hat{\theta}=rd\theta\,\hat{\theta}$ um deslocamento infinitesimal ao longo da circunferência de raio $r$ mostrada na Figura 2. Então a circulação do campo magnético ao longo desta circunferência é
Este resultado é válido sempre e é conhecido por lei de Ampère, o análogo à lei de Gauss para o campo elétrico. A curva fechada sobre a qual a circulação é calculada é a "curva amperiana". Usando os teoremas do Apêndice 2, podemos estabelecer uma versão local para a lei de Ampère,
\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}= \int\limits_{A}\vec{\nabla}\times\vec{B}\cdot d\vec{a}= 4C_{m}\, I=4C_{m}\, \int\limits_{A}\vec{J}\cdot d\vec{a}\;\implies\; \vec{\nabla}\times\vec{B}=4C_{m}\vec{J}\end{equation}onde introduzimos o campo vetorial densidade de corrente $\vec{J}$, introduzido na Seção 3.3 (veja a Figura 3).
Exercício 3. Vamos mostrar que as componentes da densidade de corrente satisfazem equações diferenciais parciais (EDP) do tipo Poisson. Para tal, precisamos introduzir o potencial vetor na forma local da lei de Ampère e usar algumas propriedades do cálculo vetorial,
\begin{equation} \vec{\nabla}\times\vec{B}=\vec{\nabla}\times \vec{\nabla}\times\vec{A}= \vec{\nabla}\, \vec{\nabla}\cdot\vec{A}-\nabla^{2}\vec{A}=4C_{m}\vec{J}.\end{equation}Como temos a liberdade de adicionar qualquer campo vetorial com divergência nula ao potencial vetor, isto nos permite escolher um potencial vetor com divergência nula, $\vec{\nabla}\cdot\vec{A}=0$, resultando assim na equação de Poisson para o potencial vetor,
\begin{equation} \nabla^{2}\vec{A}=-4C_{m}\vec{J}.\end{equation}| Figura 1: campo devido à corrente $I$.
|
Figura 2: seção transversal ao fio.
| Figura 3: densidade de corrente. |
|---|---|---|
|
|  |
4. Indução
Vimos na Seção 3.2, usando a Relatividade Especial, como cargas elétricas em movimento (corrente elétrica) gera (induz) um campo magnético em sua vizinhança. Do ponto de vista prático, este campo magnético produzido por uma corrente elétrica gera uma força numa
carga elétrica teste em movimento que pode ser verificada experimentalmente. Essa força é idêntica à força de Lorentz, já conhecida experimentalmente usando ímãs para gerar campos magnéticos ao invés de correntes elétricas. Do ponto de vista da Relatividade
Especial, se uma carga elétrica em movimento, portanto um campo elétrico variando no tempo, gera um campo magnético, então um campo magnético variando no tempo deve gerar um campo elétrico. Em suma, no fenômeno da indução, um campo de um tipo (elétrico ou magnético) variando
induz o surgimento de um outro tipo de campo (magnético ou elétrico). Esse fenômeno da indução é um efeito relativístico. As relações entre campos variando e campos induzidos estão contidas nas duas últimas equações de Maxwell.
Vamos contextualizar. Maxwell apresentou suas equações em 1861. Einstein nos apresentou a Relatividade Especial somente em 1905. Portanto, o fenômeno da indução foi descoberto experimentalmente antes da Relatividade Especial. De fato, os efeitos da indução
eletromagnética foram verificados experimentalmente, de forma magistral, por Ampère em 1823 e por Faraday em 1832. Embora os efeitos elétricos e magnéticos fossem conhecidos, separadamente, há milênios, coube a Ampère e Faraday mostrar suas inter-relações pela primeira vez. A Relatividade Especial reforçou estas inter-relações.
4.1. Ampère
Oersted descobriu experimentalmente em 1820 que um fio transportando uma corrente elétrica produzia um campo magnético. Ele usou uma bússola para identificar (após três anos) que este campo magnético era circular ao fio, como vimos na Seção 3.2. Na época, definia-se campo magnético pela interação com uma bússola. Ímãs erão conhecidos há muito tempo e interagiam com bússolas (contendo também um ímã). Este experimento de Oersted mostrou pela primeira vez uma relação explícita entre os fenômenos elétricos (corrente) é magnéticos (ímãs). Uma simulação desse experimento pode ser vista abaixo (ou aqui) na aba eletroímã.
Ampère nasceu em uma família rica e teve sua educação inteiramente em sua casa. Tornou-se professor de Matemática, Física e Química. Ainda em 1820 tomou conhecimento do experimento de Oersted e se dedicou a ele com tanto afinco ao ponto de traduzi-lo
matematicamente no que chamamos hoje de lei de Ampère, corretíssima para correntes estáticas. Infelizmente ele não registrou seus passos nesta empreitada, publicou apenas seus resultados (de forma completa em 1826, um ano antes de sua morte). Ampére
chegou a conjecturar cargas elétricas em movimento como a origem de campos magnéticos, quase um século antes do advento da Teoria da Relatividade Especial. Mais detalhes sobre Ampère podem ser obtidos aqui.
Ampère foi capaz de mostrar que a circulação do campo magnético \(\vec{B}\) de uma corrente elétrica $I$ (estática; que não varia no tempo) em um fio retilíneo, circulação em torno desse fio, é proporcional à corrente elétrica que ele transporta:
\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}= 4C_{m}\, I,\quad C_{m}=\frac{\mu_{0}}{4\pi}.\end{equation}Este resultado é válido sempre e é conhecido por lei de Ampère, o análogo à lei de Gauss para o campo elétrico. A curva fechada sobre a qual a circulação é calculada é a "curva amperiana".
Usando os teoremas do Apêndice 2, podemos estabelecer uma versão local para a lei de Ampère,
\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}= \int\limits_{A}\vec{\nabla}\times\vec{B}\cdot d\vec{a}= 4C_{m}\, I=4C_{m}\, \int\limits_{A}\vec{J}\cdot d\vec{a}\;\implies\; \vec{\nabla}\times\vec{B}=4C_{m}\vec{J},\end{equation}onde o campo vetorial densidade de corrente $\vec{J}$ foi introduzido na Seção 3.3 (veja a Figura 2 na Tabela 1). Maxwell em 1861 notou que este resultado
é compatível com a equação da continuidade (derivada na Seção 3.3) somente para campos estático (independentes do tempo), pois
onde $\rho$ é a densidade de cargas elétricas (dependente da posição e do tempo). A primeira igualdade é válida sempre ($\vec{\nabla}\cdot\vec{\nabla}=0$). Desta forma, Maxwell "corrigiu" a lei de Ampère (local) para
\begin{equation} \vec{\nabla}\times\vec{B}=4C_{m}\vec{J}+\frac{C_{m}}{C_{e}}\frac{\partial\vec{E}}{\partial t},\end{equation}obtendo assim a terceira equação de Maxwell. Note que a variação espacial do campo magnético está relacionada com a variação temporal do campo elétrico. É um campo induzindo outro.
Exercício 1. Como ao usar a lei de Gauss, use argumentos de simetria e a lei de Ampère para obter o campo magnético produzido por uma corrente $I$ (estática) em um fio retilíneo.
Exercício 2. Aplique o divergente na terceira equação de Maxwell e mostre que ela é consistente com a primeira equação de Maxwell e com a equação da continuidade.
| Figura 1
|
Figura 2
|
|---|---|
|
|
4.2. Faraday
História. Logo após a descoberta de Oersted de 1820 (relatada na seção anterior), Faraday também se dedicou ao assunto. Ao contrário de seu contemporâneo Ampère, Faraday nunca teve educação formal, substituída pela necessidade de trabalhar desde muito cedo. No entanto isso não o impediu de obter conhecimentos por si mesmo, iniciando em Química e terminando no Eletromagnetismo, proporcionando-lhe títulos honorários e várias premiações, além de uma posição como Professor. Iniciando em 1821, Faraday meticulosamente realizou uma série de experimentos sobre eletricidade e magnetismo (inspirado por Oersted e, principalmente, por Ampère) que resultou na indução eletromagnética, base para a geração de energia elétrica a partir de movimento mecânico (usina hidrelétrica). Recomendo a leitura da Seção 7.1 de Purcell-Morin para perceber a genialidade de Faraday na realização de seus experimentos e conclusões estabelecidas. A grandeza de Faraday aumenta ainda mais se levarmos em conta que suas conclusões foram obtidas apenas com base experimental, sem o embasamento matemático familiar a Ampère.
Experimentos. A simulação mostrada abaixo (ou aqui) ilustra as conclusões de Faraday. Segure e arraste o ímã (aquele com as quatro setas indicadoras de movimento) e introduza-o dentro da bobina (fio enrolado na forma circular; espiras) para induzir uma corrente elétrica no fio (que acenderá uma lâmpada). O sentido e a intensidade da corrente elétrica induzida são indicados pelo medidor de tensão (volts). Note que é necessário haver movimento do ímã (fonte de campo magnético) para induzir uma corrente elétrica no fio. Quanto mais rápido, maior a corrente. Note que invertendo o sentido do movimento do ímã, inverte-se também o sentido da corrente. Experimente.
Experimente também com o item "Linhas de campo" ligado, para visualizar as linhas de campo (do campo magnético criado pelo ímã). Essas linhas de campo foram inventadas por Faraday, mesmo sem ter os devidos conhecimentos matemáticos sobre campos vetoriais.
Experimente também com uma bobina com menos espiras: quanto mais espiras, maior a intensidade da corrente.
Lei de Faraday: a corrente induzida no fio depende diretamente da variação do fluxo do campo magnético. Faraday que não tinha conhecimentos de campos vetoriais, inventou suas "linhas de campo" para chegar a esta conclusão.
Teoria. Maxwell (1861) usou os experimentos de Faraday e deu a eles uma interpretação matemática. Para criar a corrente no fio é necessário uma força agindo nos portadores de carga. Seja uma carga \(q\) submetida a uma força $\vec{F}$. Então podemos introduzir um campo elétrico: $\vec{E}=\vec{F}/q$. Denominemos de "força eletromotriz'', por razões históricas, o trabalho por unidade de carga,
\begin{equation} \mathcal{E}=\frac{1}{q}\int\limits_{C}\vec{F}\cdot d\vec{l}= \int\limits_{C}\vec{E}\cdot d\vec{l}, \end{equation}onde $d\vec{l}$ é o deslocamento infinitesimal ao longo da trajetória $C$ da carga $q$. Note que $\mathcal{E}$ é um escalar e não um vetor (necessário para ser uma força) com dimensões de energia por unidade de carga. Segundo Maxwell, a lei de Faraday pode ser escrita como
\begin{equation} \mathcal{E}=-\frac{d\Phi}{dt},\quad \Phi=\int\limits_{A}\vec{B}\cdot d\vec{a}, \end{equation}onde $\Phi$ é o fluxo do campo magnético $\vec{B}$ através da superfície de área $A$, apoiada em um contorno $C$ por onde movimentam os portadores de carga.
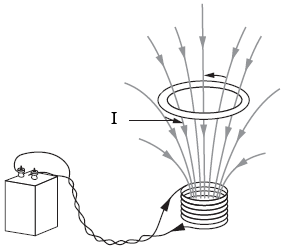
Desta vez o sinal negativo na lei de Faraday não é uma simples escolha, mas uma exigência experimental. Usando a lei de Ampère, esta corrente induzida cria um campo magnético (de simetria circular) em torno do fio sempre no sentido de compensar (graças ao sinal negativo) a variação do fluxo do campo magnético externo. A Figura 1 ilustra essa interpretação, conhecida por lei de Lenz. Nesta figura, um campo magnético (não uniforme espacialmente) é criado pelas bobinas ligadas a um gerador de corrente, de acordo com a lei de Ampère. Uma outra bobina circular (anel) é permitida se movimentar (na direção vertical) na presença deste campo magnético, variando o fluxo no seu interior. Quanto mais densa a região em termos de linhas de campo, mais intenso é o campo. Assim, esse campo magnético é mais intenso na região próximas às bobinas que o criaram. Quando o anel se aproxima da região onde o campo é mais intenso, o fluxo através dele aumenta. Segundo a lei de Lenz, uma corrente será induzida nesse anel no sentido de criar outro campo magnético que irá compensar esse aumento do fluxo do campo magnético original. Por isso o sentido da corrente induzida $I$ indicado nessa figura (veja na Figura 2 o sentido do campo criado pela lei de Ampère).
| Figura 1: Lei de Lenz (exemplo). |
Figura 2: lei de Ampère (sinal). |
|---|---|
 |
 |
Usando os teoremas do Apêndice 2, podemos estabelecer uma versão local para a lei de Faraday, a quarta equação de Maxwell,
\begin{equation} \mathcal{E}=\oint\limits_{C}\vec{E}\cdot d\vec{l}= \int\limits_{A}\vec{\nabla}\times\vec{E}\cdot d\vec{a}= -\frac{d\Phi}{dt}= \frac{d}{dt}\int\limits_{A}\vec{B}\cdot d\vec{a} \;\implies\; \vec{\nabla}\times\vec{E}=-\frac{d\vec{B}}{dt}, \end{equation}onde a superfície de área $A$ está inteiramente apoiada no contorno $C$. Vale lembrar que um campo elétrico dependente do tempo não produz um trabalho nulo numa trajetória fechada (ou seja, se for dependente do tempo, não será conservativo). Note que tomando o divergente da quarta equação de Maxwell, resulta a segunda equação de Maxwell, $\vec{\nabla}\cdot\vec{B}=0$. Note que a variação temporal de um campo magnético induz a variação espacial de um campo elétrico. É um campo induzindo o surgimento de outro.
Exercício 1. Aplique o divergente na quarta equação de Maxwell e obtenha a segunda equação de Maxwell, $\vec{\nabla}\cdot\vec{B}=0$.
Exercício 2. Reobtenha a lei de Faraday a partir da variação do fluxo do campo magnético.
5. Equações de Maxwell
Localmente (ou não), as equações de Maxwell podem ser divididas em dois grupos. O grupo ligado a cargas (divergente),\(\)
\begin{equation} \vec{\nabla}\cdot\vec{E}=4\pi C_{e}\,\rho,\quad \vec{\nabla}\cdot\vec{B}=0, \end{equation}e o grupo ligado à indução (rotacional),
\begin{equation} \vec{\nabla}\times\vec{B}= +\frac{1}{c^2}\frac{\partial\vec{E}}{\partial t} + 4\pi C_{m}\vec{J},\quad \vec{\nabla}\times\vec{E}= -\frac{\partial\vec{B}}{\partial t}. \end{equation}As constantes elétrica e magnética são
\begin{equation} C_{e}=\frac{1}{4\pi\epsilon_{0}},\quad C_{m}=\frac{\mu_{0}}{4\pi},\quad \frac{C_{e}}{C_{m}}=\frac{1}{\epsilon_{0}\mu_{0}}=c^{2}, \end{equation}onde os valores da permissividade $\epsilon_{0}$ e da permeabilidade $\mu_{0}$ do vácuo são dados na Introdução e a relação com a velocidade da luz
$c$ é deduzida na próxima subseção.
Esse grupo ligado à indução pode ser reescrito numa forma mais simétrica (verifique),
\begin{equation} \frac{1}{c}\frac{\partial\vec{E}}{\partial t}- \vec{\nabla}\times(c\vec{B})=-4\pi C_{m}(\vec{J}/c),\quad \frac{1}{c}\frac{\partial(c\vec{B})}{\partial t}+ \vec{\nabla}\times\vec{E}=0. \end{equation}Assim, os campos elétrico $\vec{E}$ e magnético (rebatizado) $c\vec{B}$ têm as mesmas dimensões (verifique).
É muito interessante utilizar aqui o potencial escalar $\phi$, introduzido na Seção 2.2, e o potencial vetorial $\vec{A}$, introduzido na Seção 3.4. No entanto, como os campos considerados aqui são dependentes do tempo, temos de verificar se alguma correção precisa ser feita nas relações já estabelecidas envolvendo estes potenciais. Para o campo magnético satisfazendo a segunda equação de Maxwell, $\vec{\nabla}\cdot\vec{B}=0$, continuamos com $\vec{B}=\vec{\nabla}\times\vec{A}$. Para o campo elétrico, devido às equações de Maxwell ligadas à indução, precisamos corrigir a relação $\vec{E}=-\vec{\nabla}\phi$, válida somente para campos estáticos. Para tal, vamos usar a quarta equação de Maxwell (lei de Faraday),
\begin{equation} \frac{\partial\vec{B}}{\partial t}+ \vec{\nabla}\times\vec{E}=\vec{\nabla}\times \left(\frac{\partial\vec{A}}{\partial t}+ \vec{E}\right)=0\;\implies\; \frac{\partial\vec{A}}{\partial t}+\vec{E}= -\vec{\nabla}\phi, \end{equation}a qual nos obriga a acrescentar a variação temporal da densidade de corrente. Desta forma, em termos dos potenciais, os campos são
\begin{equation} \vec{E}=-\vec{\nabla}\phi-\frac{1}{c}\frac{\partial(c\vec{A})}{\partial t},\quad \vec{B}=\vec{\nabla}\times\vec{A}. \end{equation}
Exercício. Elabore cuidadosamente as provas omitidas sob a etiqueta "verifique".
5.1. Onda eletromagnética
Maxwell mostrou que luz é uma onda eletromagnética e que pode se propagar no vácuo (algo inaceitável para a época, pois acreditava-se que toda onda precisava de um meio para se propagar). Para tal, Maxwell considerou suas equações no vácuo (ausência de cargas elétricas, \(\rho=0\), e de correntes, $\vec{J}=0$):
\begin{equation} \vec{\nabla}\cdot\vec{E}=0,\quad \vec{\nabla}\cdot\vec{B}=0,\quad \vec{\nabla}\times\vec{B}= +\frac{C_{m}}{C_{e}}\frac{\partial\vec{E}}{\partial t},\quad \vec{\nabla}\times\vec{E}= -\frac{\partial\vec{B}}{\partial t}. \end{equation}Maxwell, inicialmente, usou as constantes $C_{e}$ (elétrica) e $C_{m}$ (magnética). Tomemos o rotacional das duas últimas equações,
\begin{equation} \vec{\nabla}\times\vec{\nabla}\times\vec{B} =\frac{C_{m}}{C_{e}} \vec{\nabla}\times\left(\frac{\partial\vec{E}}{\partial t}\right)= \frac{C_{m}}{C_{e}}\frac{\partial}{\partial t}\vec{\nabla}\times\vec{E},\quad \vec{\nabla}\times\vec{\nabla}\times\vec{E} = \vec{\nabla}\times\left(-\frac{\partial\vec{B}}{\partial t}\right)=-\frac{\partial}{\partial t}\vec{\nabla}\times\vec{B}, \end{equation}onde pressupomos que os campos sejam suáveis, e as simplifiquemos usando $\vec{\nabla}\times(\vec{\nabla}\times\vec{A}) = \vec{\nabla}(\vec{\nabla}\cdot\vec{A}) - \nabla^{2}\vec{A}$, bem como as duas primeiras equações de Maxwell (divergência nula),
\begin{equation} -\nabla^{2}\vec{B}= \frac{C_{m}}{C_{e}}\frac{\partial}{\partial t}\vec{\nabla}\times\vec{E},\quad -\nabla^{2}\vec{E}=-\frac{\partial}{\partial t}\vec{\nabla}\times\vec{B}. \end{equation}Agora usemos novamente as duas últimas equações de Maxwell para substituir os rotacionais por derivadas temporais (e desacoplar as equações),
\begin{equation} \left(\nabla^{2} -\frac{C_{m}}{C_{e}}\frac{\partial^2}{\partial t^2}\right)\{\vec{E}\,\text{ou}\,\vec{B}\}=0. \end{equation}Esta equação diferencial parcial satisfeita pelos campos $\vec{E}$ e $\vec{B}$ é conhecida por equação de onda (no vácuo),
onde $v$ é a velocidade de propagação da onda $\psi$. Assim, Maxwell imediatamente identificou que os campos eletromagnéticos $\vec{E}$ e $\vec{B}$ satisfazem a mesma equação de onda, com a velocidade $v^2=C_{e}/C_{m}$, cujo valor coincidia com o valor da velocidade da luz na época. Maxwell não teve dúvidas: luz é uma onda eletromagnética e, pasmem, propaga-se no vácuo! As implicações conceituais e tecnológicas foram dantescas.
5.2. Simetria de calibre
Uma vez que os campos elétrico \(\vec{E}\) e magnético $c\vec{B}$ satisfazem, individualmente, uma equação de onda, os respectivos potenciais também devem satisfazê-la. Para verificarmos, vamos substituir nas equações de Maxwell os campos pelos seus potenciais,
\begin{equation} \vec{E}=-\vec{\nabla}\phi-\frac{1}{c}\frac{\partial(c\vec{A})}{\partial t},\quad \vec{B}=\vec{\nabla}\times\vec{A}. \end{equation}Como já usamos a segunda e a quarta das equações de Maxwell, resta para usarmos a quarta equação (verifique),
\begin{equation} \vec{\nabla}\times\vec{B}-\frac{1}{c^2}\frac{\partial\vec{E}}{\partial t}= \frac{1}{c^2}\frac{\partial^{2}\vec{A}}{\partial t^{2}}- \nabla^{2}\vec{A}+ \vec{\nabla}\left( \vec{\nabla}\cdot\vec{A}+\frac{1}{c^{2}}\frac{\partial\phi}{\partial t}\right)= 4\pi C_{m}\vec{J}, \end{equation}onde usamos $\vec{\nabla}\times(\vec{\nabla}\times\vec{A}) = \vec{\nabla}(\vec{\nabla}\cdot\vec{A}) - \nabla^{2}\vec{A}$. Este resultado pode ser reescrito numa forma mais elegante,
\begin{equation} \nabla^{2}\vec{A}-\frac{1}{c^{2}} \frac{\partial^{2}\vec{A}}{\partial t^{2}}=-4\pi C_{m}\vec{J}+\vec{\nabla}\left( \vec{\nabla}\cdot\vec{A}+\frac{1}{c^{2}}\frac{\partial\phi}{\partial t}\right). \quad (\ast) \end{equation}Da terceira equação de Maxwell, temos (verifique)
\begin{equation} \vec{\nabla}\cdot\vec{E}= -\nabla^{2}\phi -\frac{\partial}{\partial t}\vec{\nabla}\cdot\vec{A}= 4\pi C_{e}\,\rho, \end{equation}ou, numa forma mais elegante,
\begin{equation} \nabla^{2}\phi-\frac{1}{c^{2}}\frac{\partial^{2}\phi}{\partial t^{2}}=-4\pi C_{e}\,\rho-\frac{\partial}{\partial t}\left(\vec{\nabla}\cdot\vec{A}+\frac{1}{c^{2}}\frac{\partial\phi}{\partial t}\right), \quad (\ast\ast) \end{equation}onde somamos e subtraímos o termo contendo a derivada temporal do potencial escalar, para atingir a mesma estrutura do resultado anterior $(\ast)$, fornecido pela quarta equação de Maxwell. Estas são as equações de onda para os potenciais, na presença de cargas e correntes. E agora a justificativa do título desta seção. As equações de onda $(\ast)$ e $(\ast\ast)$ são invariantes perante as seguintes trocas de potenciais (verifique):
\begin{equation} \phi\to \phi-\frac{\partial\xi}{\partial t},\quad \vec{A}\to \vec{A}+\vec{\nabla}\xi. \end{equation}Esse fato é conhecido por simetria de calibre. O campo escalar $\xi$ é o "calibre". Esse fato deu origem a um feito ainda maior: teorias de calibre (gauge, na língua bárbara), as quais
apresentam um apelo matemático substancial.
Quer mais? Quem achar que o termo entre parêntese nas equações $(\ast)$ e $(\ast\ast)$ certamente perdeu a fé na Matemática e também nas equações de Maxwell. Como os potenciais podem ser "calibrados", isto é, permitem uma escolha, então podemos fazer uma escolha,
\begin{equation}\vec{\nabla}\cdot\vec{A}+\frac{1}{c^{2}}\frac{\partial\phi}{\partial t}=0, \end{equation}conhecida por "calibre de Lorentz". Com esta escolha, as equações de onda para os potenciais simplificam,
\begin{equation} \nabla^{2}\vec{A}-\frac{1}{c^{2}} \frac{\partial^{2}\vec{A}}{\partial t^{2}}=-4\pi C_{m}\vec{J}, \quad (\ast) \end{equation}e
\begin{equation} \nabla^{2}\phi-\frac{1}{c^{2}}\frac{\partial^{2}\phi}{\partial t^{2}}=-4\pi C_{e}\,\rho. \quad (\ast\ast) \end{equation}Naturalmente, esta simetria de calibre também deixa invariante as relações entre os campos vetoriais e seus potenciais (verifique),
\begin{equation} \vec{E}=-\vec{\nabla}\phi-\frac{1}{c}\frac{\partial(c\vec{A})}{\partial t},\quad \vec{B}=\vec{\nabla}\times\vec{A}. \end{equation}Exercício. Elabore cuidadosamente as provas omitidas sob a etiqueta "verifique".
5.3. Forma covariante.
O Eletromagnetismo de Maxwell está intimamente interligado com a Relatividade Especial de Einstein, embora esta tenha sido descoberta (elaborada?) cerca de meio século depois. Tivemos uma pequena demonstração desta inter-relação na Seção 3.2. Ainda que de forma singela, vamos "construir" uma formulação co-variante para as equações de Maxwell. Isto significa reescrever as equações de Maxwell de forma a facilitar a verificação de que elas são invariantes perante
às transformações de Lorentz.
Vamos iniciar estabelecendo notações. A geometria não é mais a euclidiana. A geometria da Relatividade Especial é aquela estabelecida por Minkowski (hiperbólica). Tempo não é mais absoluto; junto com o espaço euclidiano tridimensional, forma o espaço-tempo
quadridimensional, onde um evento em um referencial inercial \(\mathcal{O}\) ocorrendo num "instante" $t$, na posição $(x,y,z)$, será grafado como um quadrivetor (um tensor de ordem um),
As coordenadas $x^{\mu}$ são denominadas de contra-variantes. Como a métrica deste espaço não é a identidade, teremos também as coordenadas co-variantes,
\begin{equation} x_{\mu}=\sum_{\nu=0}^{3}g_{\mu\nu}x^{\nu}=g_{\mu\nu}x^{\nu}. \end{equation}Note a soma implícita nos índices contra e co-variante designados pela mesma letra. Neste espaço, a distância infinitesimal entre dois pontos (ou eventos) é
\begin{equation} (ds)^{2}=(cdt)^{2}-(dx)^{2}-(dy)^{2}-(dz)^{2} = \sum_{\mu,\nu=0}^{3}g_{\mu\nu}\,dx^{\mu}dx^{\nu} = dx_{\mu}dx^{\mu}, \end{equation}onde a métrica $g_{\mu\nu}$ é diagonal,
\begin{equation} g_{00}=-g_{11}=-g_{22}=-g_{33}=1. \end{equation}Esta forma de calcular a distância infinitesimal e o fato dela ser invariante perante às transformações de Lorentz define a geometria deste espaço (espaço de Minkowski).
Note a presença da velocidade da luz, $c$, sempre multiplicando o tempo $t$, para formar $x^{0}=ct$, no grupo das equações de Maxwell ligado à indução,
\begin{equation} \frac{1}{c}\frac{\partial\vec{E}}{\partial t}- \vec{\nabla}\times(c\vec{B})=-4\pi C_{m}(\vec{J}/c),\quad \frac{1}{c}\frac{\partial(c\vec{B})}{\partial t}+ \vec{\nabla}\times\vec{E}=0. \end{equation}Assim, os campos elétrico $\vec{E}$ e magnético (rebatizado) $c\vec{B}$ têm as mesmas dimensões. Isso sugere "rebatizarmos" também a densidade de corrente para $\vec{J}/c$, a qual passa a ter as mesmas dimensões de densidade de carga (verifique). Note que tudo está confluindo para percebermos que as equações de Maxwell vivem no espaço de Minkowski. Tem mais. Tomando o divergente da equação de Maxwell que tem o rotacional do campo magnético e usando a primeira equação de Maxwell para introduzir a densidade da cargas, obteremos a equação da continuidade (verifique), introduzida primeiramente na Seção 3.3 como uma lei de conservação (da carga elétrica),
\begin{equation} \frac{1}{c}\frac{\partial\rho}{\partial t}+\vec{\nabla}\cdot(\vec{J}/c)=0. \end{equation}Esta equação está "implorando" para definirmos um quadrivetor densidade $(J^{\nu})$:
\begin{equation} \partial_{\nu}J^{\nu}=\frac{\partial J^{0}}{\partial x^{0}}+\frac{\partial J^{1}}{\partial x^{1}}+\frac{\partial J^{2}}{\partial x^{2}}+\frac{\partial J^{3}}{\partial x^{3}}=\frac{1}{c}\frac{\partial\rho}{\partial t}+\vec{\nabla}\cdot(\vec{J}/c)=0,\quad (J^{\nu})=(\rho,J_{x}/c,J_{y}/c,J_{z}/c). \end{equation}Ou seja, o quadridivergente da quadridensidade igual a zero, $\partial_{\nu}J^{\nu}=0$, é a forma co-variante da conservação da carga no espaço-tempo de Minkowski.
Outra equação que também está implorando para ser reescrita na forma covariante é o calibre de Lorentz, introduzido na Seção 5.2,
\begin{equation} \frac{1}{c}\frac{\partial\phi}{\partial t}+\vec{\nabla}\cdot(c\vec{A})= \frac{\partial A^{0}}{\partial x^{0}}+\frac{\partial A^{1}}{\partial x^{1}}+\frac{\partial A^{2}}{\partial x^{2}}+\frac{\partial A^{3}}{\partial x^{3}}= \partial_{\nu}A^{\nu}=0,\quad (A^{\nu})=(\phi,cA_{x},cA_{y},cA_{z}). \end{equation}Desta vez definimos o quadrivetor potencial $(A^{\nu})$. A versão covariante do calibre de Lorentz afirma que o quadridivergente do quadripotencial é nulo. Seria outra lei de conservação? Ou simplesmente a conservação da carga (elétrica) em termos dos potenciais? Seguindo a mesma linha, a versão covariante da simetria de calibre é
\begin{equation} A_{\mu}\to A_{\mu}-\partial_{\mu}(c\xi). \end{equation}Note aqui os índices covariantes. Resumo até aqui: densidade de carga (campo escalar) se junta com densidade de corrente (campo vetorial) para formar o quadrivetor densidade; potencial escalar (campo escalar) se junta com potencial vetor (campo vetorial) para formar o quadrivetor potencial. Usando estes dois quadrivetores, a versão covariante das equações de ondas $(\ast)$ e $(\ast\ast)$ para os potenciais, com o calibre de Lorentz, introduzidas na Seção 5.2, é (verifique)
\begin{equation} \partial_{\mu}\partial^{\mu}A^{\nu}=4\pi C_{m}\,J^{\nu}. \end{equation}E os campos elétrico e magnético, o que eles formam no espaço-tempo de Minkowski? Como já temos os potenciais no espaço-tempo, vamos usá-los para tentarmos uma versão co-variante para os campos. Para tal, usemos as relações entre os campos e seus potenciais,
\begin{equation} \vec{E}=-\vec{\nabla}\phi-\frac{1}{c}\frac{\partial(c\vec{A})}{\partial t},\quad \vec{B}=\vec{\nabla}\times\vec{A}. \end{equation}A equação do campo elétrico pode ser reescrita assim:
\begin{equation} E_{i}=-\frac{\partial\phi}{\partial x^{i}}-\frac{1}{c}\frac{\partial(cA_{i})}{\partial t}=-\frac{\partial A_{0}}{\partial x^{i}}-\frac{\partial(cA_{i})}{\partial x^{0}}=-\frac{\partial A_{0}}{\partial x^{i}}+\frac{\partial(A_{i})}{\partial x^{0}},\end{equation}onde estamos usando o quadrivetor potencial na última igualdade. Não se deixe levar pelo fato de usarmos a mesma letra para indicar o potencial vetor $A_{i}$ e o quadrivetor potencial $A_{i}\to -cA_{i}$. O resultado acima sugere definirmos um campo eletromagnético $F_{\mu\nu}$ por uma matriz anti-simétrica (tensor de ordem dois),
\begin{equation} F_{\mu\nu}=\frac{\partial A_{\nu}}{\partial x^{\mu}}-\frac{\partial A_{\mu}}{\partial x^{\nu}}=\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu}. \end{equation}Verifique que esta matriz assume as formas
\begin{equation} (F_{\mu\nu})=\begin{pmatrix} 0 & E_{1} & E_{2} & E_{3}\\ & 0 & -cB_{3} & cB_{2}\\ & & 0 & -cB_{1}\\ & & & 0 \end{pmatrix},\quad (F^{\mu\nu})=\begin{pmatrix} 0 & -E_{1} & -E_{2} & -E_{3}\\ & 0 & -cB_{3} & cB_{2}\\ & & 0 & -cB_{1}\\ & & & 0 \end{pmatrix}. \end{equation}Impressionante! Os campos vetoriais elétrico e magnético se juntam para formar um objeto único (um tensor de ordem dois) no espaço de Minkowski.
Exercício. Elabore cuidadosamente as provas omitidas sob a etiqueta "verifique".
6. Apêndices
Estes apêndices apresentam informações a serem usadas como ferramentas nas discussões do curso. Há definições e teoremas, muito dos quais não serão demonstrados, apenas apresentados.6.1. Análise dimensional
Unidades de medida são importantes e indispensáveis. De forma geral, procuraremos expressar todas as nossas quantidades em unidades derivadas de quatro grandezas fundamentais: comprimento (L), tempo (T), massa (M) e carga elétrica (Q).
Em processos de medidas, estas grandezas são conhecidas também por dimensões. Em geral, falaremos da análise dimensional de uma determinada quantidade. Vários sistemas de medidas foram criados para expressar a intensidade de cada uma destas
quatro dimensões fundamentais. Usaremos com mais frequência o Sistema Internacional (SI ou MKS), onde comprimento é medido em metros (m), tempo em segundos (s), massa em kilogramas (kg) e carga elétrica em Coulombs (C).
Existe um procedimento padrão para analisarmos as dimensões de uma determinada quantidade de interesse: uma equação com o lado esquerdo expressando a quantidade \(B\) a ser analisada, via a notação \([B]\), e um lado direito contendo apenas as operações
de multiplicação e potenciação envolvendo as dimensões L, T, M e Q. Vejamos alguns exemplos.
O vetor posição \(\vec{r}\) tem dimensão de comprimento (L). Escrevemos matematicamente esta informação como
\begin{equation}
[\vec{r}]=\text{L}.
\end{equation}
O vetor velocidade tem dimensões de comprimento por tempo,
\begin{equation}
[\vec{v}]=\biggl[\frac{d\vec{r}}{dt}\biggr] =
\frac{\text{L}}{\text{T}}= \text{LT}^{-1}.
\end{equation}
O vetor aceleração tem dimensões de comprimento por tempo ao quadrado,
\begin{equation}
[\vec{a}]=\biggl[\frac{d^{2}\vec{r}}{dt^{2}}\biggr] =
\frac{\text{L}}{\text{T}^{2}}=\text{LT}^{-2}.
\end{equation}
As dimensões do momentum linear são
\begin{equation}
[\vec{p}]=\bigl[m\vec{v}\bigr] = \frac{\text{ML}}{\text{T}}=
\text{MLT}^{-1}.
\end{equation}
Seguindo estes exemplos, a análise dimensional do vetor força na segunda lei de Newton (massa constante) nos fornece
\begin{equation}
[\vec{F}]=\bigl[m\vec{a}\bigr] = \frac{\text{ML}}{\text{T}^{2}}=
\text{MLT}^{-2} \text{(Newton)}.
\end{equation}
Newton é a unidade de força no sistema MKS.
Quais são as dimensões da constante \(C_{e}\) aparecendo na expressão para a força elétrica (lei de Coulomb)
\begin{equation}
\label{eq:Coulomb2}
\vec{F}_{e}=C_{e}\frac{Qq}{r^{2}}\hat{r}
\end{equation}
entre duas cargas elétricas \(Q\) e \(q\) separadas pela distância \(r\)? Seguindo o modelo anterior, temos
\begin{equation}
\label{eq:aCe}
[C_{e}]=\text{NL}^{2}\text{Q}^{-2}=\text{ML}^{3}\text{T}^{-2}\text{Q}^{-2}.
\end{equation}
Por completeza, devemos mencionar que cargas magnéticas nunca foram observadas. No entanto quando dois fios conduzindo correntes elétricas \(I_{1}\) e \(I_{2}\) estão a uma distância \(\rho\), podemos medir uma força por unidade de comprimento entre eles,
\begin{equation}
\label{eq:BiotSavat}
\vec{f}_{m}=2C_{m}\frac{I_{1}I_{2}}{\rho}\hat{\rho}.
\end{equation}
Esta força é conhecida como lei de Biot-Savat. Usando a definição de corrente, carga por tempo, temos
\begin{equation}
\label{eq:aI}
[I]=\biggl[\frac{dQ}{dt}\biggr] = \text{QT}^{-1}.
\end{equation}
Assim, as dimensões da constante \(C_{m}\) são
\begin{equation}
\label{eq:aCm}
[C_{m}]=\text{NT}^{2}\text{Q}^{-2}=\text{MLQ}^{-2}.
\end{equation}
Podemos notar também então que a razão \(C_{e}/C_{m}\) tem a mesma dimensão de velocidade ao quadrado. De fato, Maxwell mostrou que no vácuo, a velocidade da luz (onda eletromagnética) é
\begin{equation}
\label{eq:veluz}
c=\sqrt{\frac{C_{e}}{C_{m}}}.
\end{equation}
Os valores destas constantes (no vácuo) são: \(C_{e}=8.987\,551\,788\times 10^{9}\) N\(\cdot\)m\(^{2}\)/C\(^{2}\) e \(C_{m}=10^{-7}\) N\(\cdot\)s\(^{2}\)/C\(^{2}\). Portanto, medindo as constantes \(C_{e}\) e \(C_{m}\) podemos calcular a velocidade da luz. Este resultado está entre os mais surpreendentes acerca da nossa natureza. As surpresas não param aqui, há ainda um fato ainda mais marcante sobre o comportamento da luz: ela é um limite superior para a velocidade de qualquer quantidade em movimento. No presente tempo, conseguimos dar uma velocidade próxima à da luz (98%) apenas para partículas sub-atômicas como o elétron.
A força de Lorentz,
\begin{equation}
\label{eq:db}
\vec{F} = q\,\vec{v}\times\vec{B},
\end{equation}
produzida por uma carga \(q\) em movimento com uma velocidade \(\vec{v}\) em um campo magnético \(\vec{B}\), é responsável por trajetórias helicoidais. As dimensões do campo magnético \(\vec{B}\) são
\begin{equation}
\label{eq:db2}
[\vec{B}]=\biggl[\frac{||\vec{F}||}{q||\vec{v}||}\biggr] =
\text{MQ}^{-1}\text{T}^{-1} \text{(Tesla)}.
\end{equation}
6.2. Gradiente, Rotacional e Divergente
Gradiente. Considerando um campo escalar \(\phi=\phi(x,y,z)\), a sua diferencial (total) é
\(\displaystyle d\phi=\frac{\partial\phi}{\partial x}dx+ \frac{\partial\phi}{\partial y}dy+ \frac{\partial\phi}{\partial y}dy= \vec{\nabla}\phi\cdot d\vec{r}\),
onde introduzimos o operador (vetorial)
\(\displaystyle \vec{\nabla}=\hat{i}\frac{\partial}{\partial x}+ \hat{j}\frac{\partial}{\partial y}+ \hat{k}\frac{\partial}{\partial y}\),
denominado de gradiente. Sua interpretação geométrica é imediata: o valor absoluto da diferencial \(d\phi\) será máximo quando o gradiente \(\vec{\nabla}\phi\) estiver alinhado com o deslocamento infinitesimal \(d\vec{r}\). O gradiente aponta a direção de maior crescimento.
Divergente. O divergente é o limite de fluxo por unidade de volume,
\(\displaystyle \text{div}\,\vec{E}=\lim\limits_{V\to 0}\frac{1}{V} \int\limits_{A\supset V}\vec{E}\cdot d\vec{a} = \vec{\nabla}\cdot\vec{E}\).
A última igualdade estabelece a sua forma operacional. A Figura da esquerda mostra uma volume finito subdividido em um número infinito de volumes infinitesimais \(V\) (envolta pela área \(A\)). A soma de todos os fluxos nestes volumes infinitesimais,
por unidade de volume, é a divergência do campo vetorial \(\vec{E}\). Note que o divergente resulta em um campo escalar.
Rotacional. O rotacional é circulação por unidade de área,
\(\displaystyle \text{rot}\,\vec{E}=\lim\limits_{A\to 0}\frac{1}{A} \int\limits_{C\supset A}\vec{E}\cdot d\vec{r}\;\hat{n}= \vec{\nabla}\times\vec{E}\).
A última igualdade estabelece a sua forma operacional. A Figura da direita mostra uma área finita subdividida em um número infinito de áreas infinitesimais \(A\) (envolta pela curva \(C\)). A soma de todos as circulações nestas curvas infinitesimais,
por unidade de área, é o rotacional do campo vetorial \(\vec{E}\). Note que o rotacional resulta em um campo vetorial.
| Volumes
|
Áreas
|
|---|---|
|
|
Fluxo: \(\displaystyle \Phi=\int\limits_{A\supset V}\vec{E}\cdot d\vec{a}\), onde \(d\vec{a}\) está na direção perpendicular ao elemento de área \(da\) e a área \(A\) é o bordo do volume \(V\).
Circulação: \(\displaystyle \int\limits_{C\supset A}\vec{E}\cdot d\vec{r}\), onde \(d\vec{r}\) é o deslocamento tangente à curva \(C\), bordo da área \(A\).
| Gradiente
|
Rotacional
|
Divergente
|
|---|---|---|
| \(\displaystyle\int\limits_{P=\partial C}d\phi = \int\limits_{C}\vec{\nabla}\phi\cdot d\vec{r}\)
|
\(\displaystyle\int\limits_{C=\partial A}\vec{E}\cdot d\vec{r} =\int\limits_{A}\vec{\nabla}\times\vec{E}\cdot d\vec{a}\)
|
\(\displaystyle\int\limits_{A=\partial V}\vec{E}\cdot d\vec{a} =\int\limits_{V}\vec{\nabla}\cdot\vec{E}\, dV\)
|
|
|
|
6.3. Delta de Dirac
O que, comumente, chamamos de "função'' \(\delta(x)\), introduzida por Dirac em 1930, é algo além, uma "função generalizada'' ou uma distribuição, definida por
\begin{equation} \delta(x-a)[\phi]\equiv\int_{-\infty}^{+\infty}\phi(x)\,\delta(x-a)\,dx =\phi(a). \end{equation}Note que precisamos de uma função auxiliar ($\phi$) para revelar a ação da distribuição. A função arbitrária $\phi(x)$, conhecida como suporte, precisa possuir duas propriedades:
- ser suave e possuir todas as suas derivadas (ser analítica de classe infinita);
- ter um suporte compacto (ser igual a zero fora de um intervalo limitado).
A distribuição definida acima tem algumas propriedades gerais, independentes de ser a delta de Dirac:
- ela é um funcional linear (transforma funções em números), \begin{equation} \delta[\alpha\,\phi+\beta\,\psi] = \alpha\,\delta[\phi] + \beta\,\delta[\psi],\quad \alpha,\beta\in\mathbb{R};\end{equation}
- a derivada dela é outra distribuição, \begin{equation}\delta'[\phi] = -\delta[\phi'];\end{equation}
- ela é homogênea de grau um e par, \begin{equation}\delta(\alpha x)[\phi] = \frac{\delta(x)[\phi]}{|\alpha|};\end{equation}
- a composição dela com uma função $g(x)$ é \begin{equation}\delta(g(x)) = \sum_{i}\frac{\delta(x-x_{i})}{|g'(x_{i})|},\quad g(x_{i})=0,\; g'(x_{i})\neq 0,\end{equation} onde as raízes devem ser simples;
- a sua versão tridimensional é o produto de distribuições, \begin{equation}\delta(\vec{r})=\delta(x)\delta(y)\delta(z).\end{equation}
Exercício 1. Mostre que o laplaciano de $1/r$ ($r\geq 0$) é uma distribuição (delta de Dirac). O laplaciano, $\Delta=\nabla^{2}=\vec{\nabla}\cdot\vec{\nabla}$, da função $1/r$, onde $r$ é a norma do vetor radial, tem uma conexão direta com a distribuição \(\delta\) de Dirac, a qual é muito útil em Eletromagnetismo. Primeiro é necessário notar que a ação do laplaciano em $1/r$ não está definida somente na origem ($r=0$),
\begin{equation} \nabla^{2}\frac{1}{r} = \frac{1}{r^{2}}\frac{d}{dr}\left(r^{2}\frac{d}{dr}\right)\frac{1}{r}=0, \quad r\neq 0. \end{equation}Segundo, como a função suporte $\phi$ é regular, ela admite uma série de Taylor em torno de $r=0$,
\begin{equation}\phi(x,y,z)=\phi(0) + \sum_{i=1}^{3}\frac{\partial\phi}{\partial x_{i}}(0)\, x_{i} + \sum_{i,j=1}^{3}\frac{\partial^{2}\phi} {\partial x_{i}\partial x_{j}}(0)\, x_{i}x_{j} + \ldots\end{equation}a qual pode ser reescrita em termos das coordenadas esféricas na forma
\begin{equation} \phi(r,\Omega)=\phi(0) + f_{1}(\Omega)\, r + f_{2}(\Omega)\, r^{2} + \ldots \end{equation}onde $\Omega$ representa as coordenadas angulares. Terceiro, precisamos de um processo de regularização,
\begin{equation} r_{\eta}=\sqrt{r^{2}+\eta^{2}},\quad \lim_{\eta\to 0}r_{\eta}=r. \end{equation}Assim,
\begin{equation} \nabla^{2}\frac{1}{r} = \lim_{\eta\to 0} \nabla^{2}\frac{1}{r_{\eta}} = -\lim_{\eta\to 0} \frac{3\eta^{2}}{r_{\eta}^{5}}. \end{equation}a qual está definida em $r=0$. Desta forma verificaremos que a ação do laplaciano em $1/r$ se comporta como uma distribuição,
\begin{equation} \nabla^{2}\frac{1}{r}[\phi] = \int\limits_{\mathbb{R}^{3}}dV\, \phi\,\nabla^{2}\frac{1}{r} = \int\limits_{\mathbb{R}^{3}/S^{2}}dV\, \phi\,\nabla^{2}\frac{1}{r} + \int\limits_{S^{2}}dV\, \phi\,\nabla^{2}\frac{1}{r} = \int\limits_{S^{2}}dV\, \phi\,\nabla^{2}\frac{1}{r} = -\lim_{\eta\to 0}\int\limits_{S^{2}}dV\, \phi(r,\Omega)\frac{3\eta^{2}}{r_{\eta}^{5}}. \end{equation}Uma pausa para alguns esclarecimentos sobre os procedimentos de integração utilizados até aqui. O espaço de integração $\mathbb{R}^{3}$ foi dividido em duas regiões: uma limitada por uma esfera unitária $S^{2}$ centrada na origem $r=0$ e o complemento $\mathbb{R}^{3}/S^{2}$, onde a ação do laplaciano é nula. Para continuarmos, trocaremos na última equação a função suporte $\phi$ pela sua série de Taylor em torno de $r=0$ e o elemento de volume por $dV=dr\, dS$, com o elemento de área $dS=r^{2}d\Omega$, onde $d\Omega=\sin\theta\, d\theta d\phi$ é o ângulo sólido compreendido pela área $dS$,
\begin{equation} \nabla^{2}\frac{1}{r}[\phi] = -\phi(0)\,\int\limits_{\partial S^{2}}d\Omega\,\lim_{\eta\to 0} \int_{0}^{1}dr\,\frac{3\eta^{2}r^{2}}{(r^{2}+\eta^{2})^{5/2}}- \sum_{k=1}^{\infty}\int\limits_{\partial S^{2}}d\Omega\, f_{k}(\Omega)\,\lim_{\eta\to 0} \int_{0}^{1}dr\,\frac{3\eta^{2}r^{2+k}}{(r^{2}+\eta^{2})^{5/2}}= -4\pi\,\phi(0). \end{equation}Note que os limites devem ser executados após as integrações (uma integral cria funções novas). A primeira integral radial tem uma forma simples,
\begin{equation} \int_{0}^{1}dr\,\frac{3\eta^{2}r^{2}}{(r^{2}+\eta^{2})^{5/2}}= \frac{1}{(1+\eta^{2})^{3/2}}. \end{equation}Os termos de potências ímpares na segunda integral radial são proporcionais a $\eta^{k+1}$ e aqueles de potências pares são proporcionais a $\eta^{2}$, o que anula completamente a contribuição desta segunda integral, após a passagem do limite $\eta\to 0$. Desta forma, interpretamos a ação do laplaciano em $1/r$: se comporta como uma distribuição (tridimensional), conhecida como delta de Dirac,
\begin{equation} \nabla^{2}\frac{1}{r} = -4\pi\,\delta(r)= -4\pi\,\delta(\vec{r}),\quad r\geq 0. \end{equation}