Anterior
Próximo

3. Campo Magnético

3.4. Potencial vetor

 A segunda equação de Maxwell tem uma solução imediata (verifique),

\begin{equation} \vec{\nabla}\cdot\vec{B}=0 \;\implies\; \vec{B}=\vec{\nabla}\times\vec{A}. \end{equation}

O campo vetorial \(\vec{A}\) é conhecido como potencial vetor. Ele desempenha um papel similar ao potencial escalar \(\phi\), tal que \(\vec{E}=-\vec{\nabla}\phi\). Note que os potenciais \(\phi\) e \(\vec{A}\) dão origem aos campos vetoriais  \(\vec{E}\) (elétrico) e \(\vec{B}\) (magnético), via gradiente e rotacional, respectivamente. Naturalmente, estes potenciais estão definidos a menos de uma constante arbitrária, pelo menos até o momento. Vale ressaltar que esta solução em termos de um potencial vetor, via rotacional, é válida somente na ausência de cargas magnéticas. Na presença de cargas magnéticas, o divergente do campo magnético não será nulo, em geral (veja a Seção 3.1).

Em geral, correntes são conduzidas em materiais que possuem extensões, além de comprimentos (como num fio). Isto significa que teremos de considerar densidades de correntes, um campo vetorial, como introduzidas na Seção 3.3.

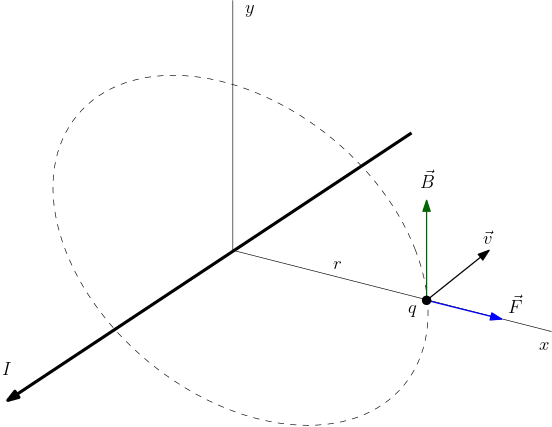
Exercício 1. Vejamos como obter o potencial vetor para o campo magnético criado por uma corrente \(I\) em um fio retilíneo. Vimos na Seção 3.2 que este campo magnético tem a forma mostrada nas Figura 1 e 2 da tabela abaixo,

\begin{equation} \vec{F}=q\,\vec{v}\times\vec{B},\; \vec{v}=-v\hat{k},\; \vec{B}=2C_{m}\frac{I}{r}\hat{\theta}.\end{equation}

Queremos encontrar o potencial vetor $\vec{A}$ tal que $\vec{B}=\vec{\nabla}\times\vec{A}$. Devida à simetria cilíndrica do fio (retilíneo), melhor usar coordenadas cilíndricas, $\vec{A}=A_{r}\hat{r}+A_{\theta}\hat{\theta}+A_{z}\hat{k}$. Também devido à esta simetria, esperamos que este potencial vetor não dependa da coordenada $z$ (ao longo do fio) e nem da coordenada angular $\theta$; cada componente do potencial vetor dever ser função somente da coordenada radial $r$, $A_{r,\theta,z}=A_{r,\theta,z}(r)$. Sabemos que o campo magnético está inteiramente na direção tangencial (direção de $\hat{\theta}$). Assim,

\begin{equation} \vec{\nabla}\times\vec{A}= \left(\frac{\partial A_{r}}{\partial z}-\frac{\partial A_{z}}{\partial r}\right)\hat{\theta}= -\frac{\partial A_{z}}{\partial r}\hat{\theta}=\vec{B}= 2C_{m}\frac{I}{r}\hat{\theta}\end{equation}

Desta forma,

\begin{equation} -\frac{\partial A_{z}}{\partial r}= 2C_{m}\frac{I}{r}\;\implies\; A_{z}=-2C_{m}I\ln r+cte.\end{equation}

O potencial vetor está ao longo do fio, $\vec{A}=A_{z}\hat{k}$, no sentido contrário à corrente $I$. Temos ainda a liberdade de adicioná-lo qualquer campo vetorial com divergência nula.

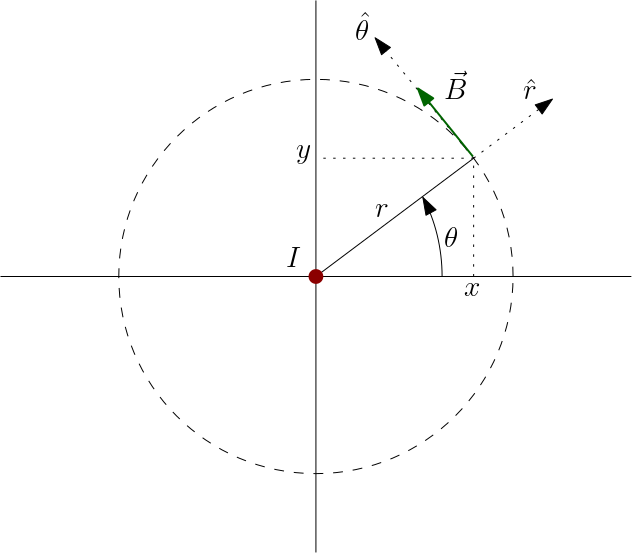
Exercício 2. Vamos mostrar que a circulação do campo magnético de uma corrente elétrica em um fio retilíneo, circulação em torno desse fio, é proporcional à corrente elétrica que ele transporta. Seja $d\vec{l}=dl\hat{\theta}=rd\theta\,\hat{\theta}$ um deslocamento infinitesimal ao longo da circunferência de raio $r$ mostrada na Figura 2. Então a circulação do campo magnético ao longo desta circunferência é

\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}= \frac{2C_{m}I}{r}r\int\limits_{0}^{2\pi}d\theta=4C_{m}\, I.\end{equation}

Este resultado é válido sempre e é conhecido por lei de Ampère, o análogo à lei de Gauss para o campo elétrico. A curva fechada sobre a qual a circulação é calculada é a "curva amperiana". Usando os teoremas do Apêndice 2, podemos estabelecer uma versão local para a lei de Ampère,

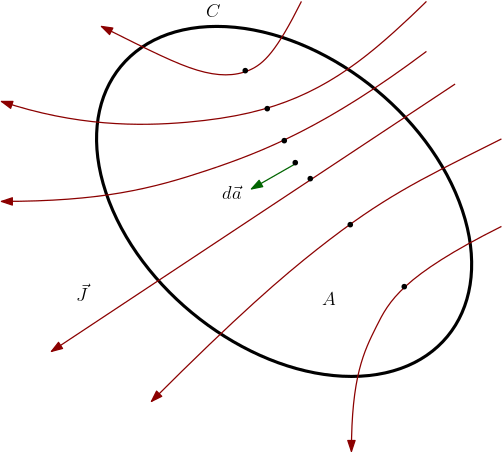
\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}= \int\limits_{A}\vec{\nabla}\times\vec{B}\cdot d\vec{a}= 4C_{m}\, I=4C_{m}\, \int\limits_{A}\vec{J}\cdot d\vec{a}\;\implies\; \vec{\nabla}\times\vec{B}=4C_{m}\vec{J}\end{equation}

onde introduzimos o campo vetorial densidade de corrente $\vec{J}$, introduzido na Seção 3.3 (veja a Figura 3).

Exercício 3. Vamos mostrar que as componentes da densidade de corrente satisfazem equações diferenciais parciais (EDP) do tipo Poisson. Para tal, precisamos introduzir o potencial vetor na forma local da lei de Ampère e usar algumas propriedades do cálculo vetorial,

\begin{equation} \vec{\nabla}\times\vec{B}=\vec{\nabla}\times \vec{\nabla}\times\vec{A}= \vec{\nabla}\, \vec{\nabla}\cdot\vec{A}-\nabla^{2}\vec{A}=4C_{m}\vec{J}.\end{equation}

Como temos a liberdade de adicionar qualquer campo vetorial com divergência nula ao potencial vetor, isto nos permite escolher um potencial vetor com divergência nula, $\vec{\nabla}\cdot\vec{A}=0$, resultando assim na equação de Poisson para o potencial vetor,

\begin{equation} \nabla^{2}\vec{A}=-4C_{m}\vec{J}.\end{equation}


Tabela Campo magnético de um fio.
Figura 1: campo devido à corrente $I$.
Figura 2: seção transversal ao fio.
 Figura 3: densidade de corrente.
 


Anterior
Próximo