Anterior
Próximo

3. Campo Magnético

3.3. Densidade de Corrente

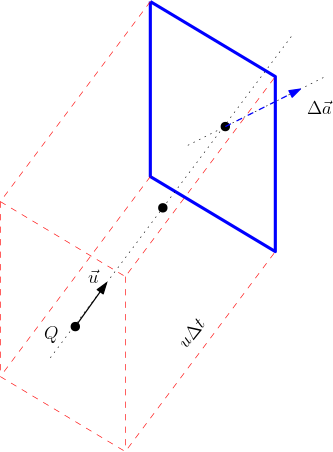
 Diferentemente do campo elétrico, que é produzido por uma carga elétrica fonte, o campo magnético não tem uma carga magnética fonte. Até o momento ainda não conseguimos observar uma carga magnética, o que coloca uma grande dúvida sobre sua existência. Nossos campo magnéticos serão criados por cargas elétricas em movimento, como vimos na Seção 3.2. Portanto precisamos definir uma densidade de cargas em movimento, como um vetor. Cargas em movimento é uma corrente elétrica. Para tal, considere a Figura 1 na Tabela Densidade de Corrente. Cada portador de cargas (pontos) tem uma carga \(Q\) é uma velocidade \(\vec{u}\) (numa região muito pequena). Consideremos as cargas que atravessarão uma determinada área \(\Delta a\) num tempo \(\Delta t\). Seja \(\Delta\vec{a}\) o vetor elemento de área. O volume apoiado na área \(\Delta a\) e de altura \(u\Delta t\) é \(\Delta V=\Delta t\,\vec{u}\cdot\Delta\vec{a}\). Seja \(n\) a densidade dos portadores de cargas nesta região (a densidade de cargas é \(\rho=nQ\)). Então o total de portadores de cargas é \(n\Delta V\). Podemos definir (localmente) corrente elétrica como carga por unidade de tempo:

\begin{equation} dI=\lim\limits_{\Delta t\to 0}\frac{n\Delta V\,Q}{\Delta t}=\rho \vec{u}\cdot d\vec{a}. \end{equation}

Podemos introduzir o campo vetorial densidade de corrente \(\vec{J}\) de modo a obtermos a corrente total \(I\) passando por uma área \(A\) como o fluxo (da densidade de corrente):

\begin{equation} I=\int\limits_{A} \vec{J}\cdot d\vec{a},\; \vec{J}=\rho\vec{u}. \end{equation}

A unidade de de corrente elétrica no Sistema Internacional (SI) é o Ampere (A=C/s). Isto faz com que a unidade de densidade de corrente seja A/m\(^{2}\) (corrente por área).

 Lei de conservação. O campo vetorial densidade de corrente \(\vec{J}\) é o campo escalar densidade de cargas estão intimamente relacionados. Para sabermos como, temos de introduzir um princípio (ou postulado): carga elétrica é conservada. Considere uma carga total \(Q\) saindo (ou entrando) de uma região de volume \(V\), na forma de uma corrente \(I=dQ/dt\). Considere uma superfície fechada, de área \(A\),  contendo o volume \(V\). A carga \(dQ=\rho\,dV\) que sai desse volume \(V\) precisa atravessar a superfície \(A\) que o contém. Assim, usando a definição de corrente elétrica e princípio da conservação da carga (ou da corrente) elétrica, temos

\begin{equation} I=\oint\limits_{A} \vec{J}\cdot d\vec{a}= -\frac{dQ}{dt}= -\frac{d}{dt}\int\limits_{V}\rho\,dV. \end{equation}

O sinal negativa indica que a carga está saindo da região. Podemos usar o teorema de Gauss para passar a integral de superfície para a integral de volume:

\begin{equation} \oint\limits_{A} \vec{J}\cdot d\vec{a}= \int\limits_{V}\vec{\nabla}\cdot\vec{J}\,dV=-\frac{d}{dt}\int\limits_{V}\rho\,dV\; \implies\; \vec{\nabla}\cdot\vec{J}+\frac{d\rho}{dt}=0. \end{equation}

Esta última equação é conhecida por equação da continuidade. Ela relaciona a variação temporal do campo escalar densidade de carga com a variação espacial (divergente) do campo vetorial densidade de corrente. Ela afirma (localmente) a conservação da carga: a carga que sai de uma região, sai na forma de uma corrente.


Tabela Densidade de Corrente.

Figura 1
Figura 2



Anterior
Próximo