Os trabalhos de Gauss em 1813 sobre Geometria deu uma excelente contribuição ao eletromagnetismo sintetizado pelas equações de Maxwell de 1861. A essência desta contribuição de Gauss, conhecida por "lei de Gauss", é a relação entre o fluxo do campo elétrico
com suas cargas fonte, válida somente para campos com uma dependência com o inverso do quadrado (exatamente) da distância.
Fluxo. Um campo vetorial como o campo elétrico pode ser visualizado pelas suas linhas de campo, as quais são formadas ligando os pontos onde os vetores prescritos pelo campo vetorial são
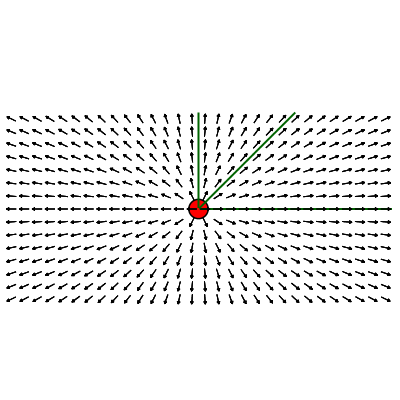
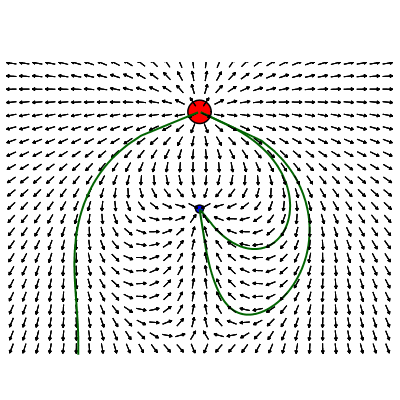
colocados de forma a serem tangentes a estas curvas. As figuras nas duas primeiras colunas da Tabela 1 ilustram as linhas de campo (no plano) para uma carga (positiva) e para duas cargas, uma positiva (vermelha) e uma negativa (azul), com carga positiva
sendo três vezes mais intensa, respectivamente. As linhas de campo são indicadas pelas curvas verdes. Note que, por definição, as linhas de campo iniciam nas cargas positivas e terminam nas cargas negativas. Agora é só extrapolar para três dimensões.
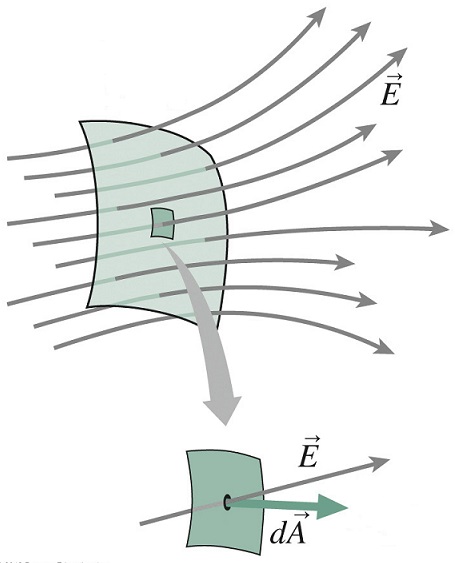
O fluxo pode ser visualizado como um número que quantifica as linhas de campo que atravessam uma determinada superfície, como mostrado na penúltima coluna da tabela acima. O fluxo é definido como
\begin{equation} \Phi=\int\limits_{A}\vec{E}\cdot d\vec{a}, \end{equation}
onde o vetor elemento de área \(d\vec{a}\) (ou \(d\vec{A}\) em algumas figuras) tem intensidade \(dA\) (elemento área) na direção perpendicular ao elemento área. A integral é feita numa área finita $A$.
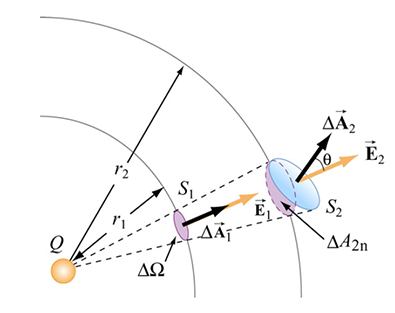
Ângulo sólido. A figura na última coluna da tabela acima mostra o chamado ângulo sólido (\(d\Omega\)), definido como
\begin{equation} d\Omega=\frac{\hat{r}\cdot d\vec{a}}{r^{2}},\quad\int\limits_{A}d\Omega=4\pi. \end{equation}
Note o ângulo sólido é a generalização tridimensional do ângulo polar no plano, o qual é \(2\pi\) para uma curva fechada (uma volta completa) em torno da origem, não importando o formato da curva. Similarmente, o ângulo sólido é \(4\pi\) para uma superfície
fechada em torno da origem, não importando o formato da curva.
Tab. 1: Linhas de campos, Fluxo e Ângulo sólido.
Uma carga positiva
|
Uma carga positiva e uma negativa
|
Fluxo |
Ângulo sólido
|
|
|
|
|
Lema de Gauss. Com estas noções de fluxo e ângulo sólido, podemos estabelecer uma relação entre as cargas fontes do campo elétrico e o seu fluxo através de uma superfície fechada contendo estas
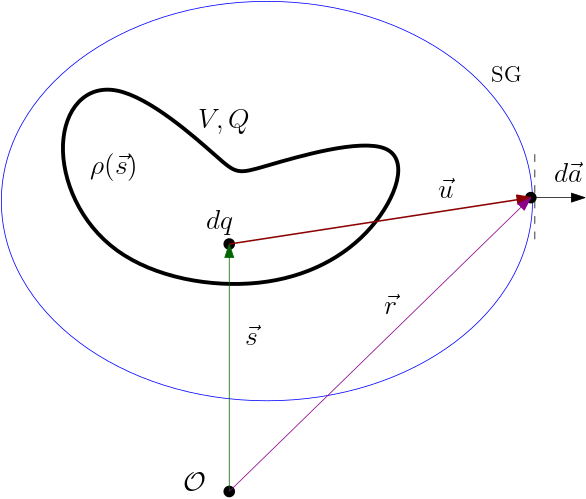
cargas. Para tal, observe a primeira figura na Tabela 2 abaixo. Ela mostra uma carga total \(Q\) distribuída num volume \(V\) segundo a densidade \(\rho(\vec{s})\), onde o vetor posição \(\vec{s}\) localiza um elemento de carga \(dq=\rho(\vec{s})dV\)
em relação ao referencial inercial (fixo) \(\mathcal{O}\). Imagine uma superfície fechada (de área total \(A\)) envolvendo esta distribuição de cargas. Esta é denominada de superfície gaussiana (SG). Imagine também um elemento de área \(d\vec{a}\) nesta
superfície gaussiana, localizado pelo vetor posição \(\vec{r}\) em relação ao mesmo referencial inercial \(\mathcal{O}\). Esse elemento de área compreende o ângulo sólido
\begin{equation} d\Omega=\frac{\hat{u}\cdot d\vec{a}}{u^{2}}, \end{equation}
onde \(\vec{u}=\vec{r}-\vec{s}\). Note que o ângulo sólido compreendido pela superfície gaussiana SG é sempre \(4\pi\), independentemente da posição do elemento de carga \(dq\), desde que SG contenha a distribuição de cargas completamente. O ângulo sólido
não depende da origem do sistema de coordenadas utilizado. Calculemos agora o fluxo (através da superfície gaussiana SG) do campo elétrico produzido por esta distribuição de cargas,
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}, \end{equation}
onde o campo elétrico na posição \(\vec{r}\) é a soma de todas as contribuições dos elementos de carga \(dq\) dentro da distribuição,
\begin{equation} \vec{E}(\vec{r})=C_{e}\int\limits_{Q}dq\frac{\vec{u}}{u^{2}}=C_{e}\int\limits_{V}dV\rho(\vec{s})\frac{\hat{u}}{u^{2}},\; \vec{u}=\vec{r}-\vec{s},\; dq=\rho(\vec{s}) dV. \end{equation}
Substituindo esta expressão no fluxo,
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}=C_{e}\int\limits_{V}dV\rho(\vec{s})\oint\limits_{A}\frac{\hat{u}\cdot d\vec{a}}{u^{2}}=C_{e}\int\limits_{V}dV\rho(\vec{s})\oint\limits_{A}d\Omega=4\pi C_{e}\int\limits_{V}dV\rho(\vec{s})=4\pi
Q.\end{equation}
Magnífico! O fluxo total, através de uma superfície fechada e arbitrária, contendo uma distribuição de cargas é simplesmente proporcional à carga total desta distribuição. Esse é o Lema de Gauss. Note que se a dependência do campo vetorial com a posição
não for exatamente o inverso do quadrado, não teríamos este resultado surpreendente. Ou seja, o Lema de Gauss é uma consequência da Lei de Coulomb.
Tab. 2: Distribuições de cargas.
| Geral |
Ponto (\(d\vec{a}=da\,\hat{r}\)) |
Esfera (\(d\vec{a}=da\,\hat{r}\)) |
Plano (\(d\vec{a}=\pm da\,\hat{k}\)) |
|
|
|
|
Exemplo 1.
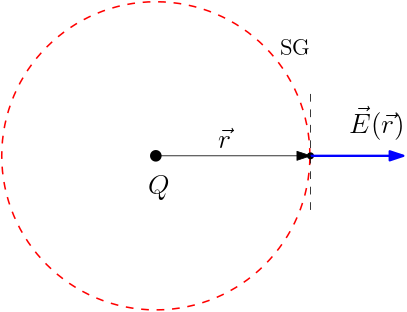
Vale manter em mente que a superfície gaussiana é arbitrária, a qual podemos escolher de acordo com nossa conveniência. Assim, podemos calcular campos elétricos de distribuições com simetria. Como exemplo, considere a segunda figura na Tabela 2, mostrando
uma carga pontual \(Q\). Como o campo elétrico de uma carga pontual tem simetria esférica, ele deve ser da forma \(\vec{E}(\vec{r})=E(r)\hat{r}\) (simetria radial). Neste caso, a melhor escolha para a superfície gaussiana (SG) é uma casca esférica de
raio \(r\). Esta escolha faz com que o campo elétrico seja perpendicular a esta superfície e paralelo ao vetor elemento de área \(d\vec{a}=da\,\hat{r}\) (sempre apontando para fora), em qualquer ponto. Portanto sabemos calcular seu fluxo através de
SG:
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}=E(r)\oint\limits_{A}da=4\pi r^{2}E(r)=4\pi C_{e}Q\;\implies\; E(r)=C_{e}\frac{Q}{r^{2}}.\end{equation}
Certamente já sabíamos deste resultado. No entanto, podemos usar o mesmo procedimento para o campo de uma distribuição esférica, cilíndrica ou plana, para citar algumas distribuições altamente simétricas.
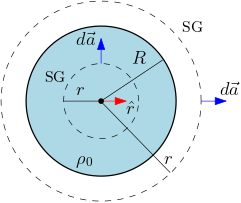
Exemplo 2. Como segundo exemplo, considere uma carga total \(Q\) distribuída numa esfera maciça de raio \(R\) através de uma densidade constante \(\rho_{0}\), mostrada na terceira figura na
Tabela 2. Estratégia. Em toda distribuição com uma densidade especificada, devemos primeiro escrever a carga total em termos dos parâmetros presentes na densidade. A densidade, em geral, assim como os elementos de volumes, áreas e comprimentos,
é função da posição. No presente caso, devido à simetria esférica da distribuição (todas as direções são idênticas), melhor usar coordenadas esféricas. Também devido à simetria esférica da distribuição, esperamos que o campo elétrico resultante seja
radial, \(\vec{E}(\vec{r})=E(r)\hat{r}\), implicando em superfícies esféricas concêntricas como superfícies gaussianas. Desta vez temos de considerar duas superfícies gaussianas (SG), uma dentro e outra fora da distribuição, como mostrado na terceira
figura na Tabela 2. Execução. Como o elemento de carga \(dq\) ocupa o elemento de volume \(dV\), a densidade de cargas é definida localmente,
\begin{equation} \rho=\frac{dq}{dV}=\rho_{0}. \end{equation}
Os elementos de área e de volume em coordenadas esféricas são:
\begin{equation} d\vec{a}=da\,\hat{r},\; da=r^{2}\sin\theta\,d\theta\,d\varphi,\; dV=da\,dr,\quad V=\int\limits_{V}dV=\int\limits_{0}^{R}r^{2}dr\int\limits_{0}^{\pi}\sin\theta\,d\theta\int\limits_{0}^{2\pi}d\varphi=\frac{4\pi}{3}R^{3}. \end{equation}
Desta forma podemos escrever o elemento de carga em termos de coordenadas e calcular a carga total,
\begin{equation} Q=\int\limits_{V}dq=\int\limits_{V}\rho(r,\theta,\varphi)dV=\rho_{0}\int\limits_{V}dV=\rho_{0}\frac{4\pi}{3}R^{3}.\; (\ast) \end{equation}
Vale observar que em geral a densidade é uma função da posição e, portanto, irá contribuir com termos que irão fazer parte dos integrandos das integrais envolvidas. No presente caso ela é constante. O próximo passo é usar o Lema de Gauss para o campo
radial \(\vec{E}(\vec{r})=E(r)\hat{r}\), ou seja, o fluxo através da superfície gaussiana externa é proporcional à carga interna a esta superfície. Primeiro, nos posicionaremos fora da distribuição (\(r>R\)). Neste caso a carga interna à superfície
gaussiana (SG) é a própria carga total \(Q\). O Fluxo total pela SG externa de raio \(r>R\) é
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}=E(r)\oint\limits_{A}da=4\pi r^{2}E(r)=4\pi C_{e}Q\;\implies\; E(r)=C_{e}\frac{Q}{r^{2}},\; r\geq R.\end{equation}
Note que este campo elétrico fora da distribuição esférica é idêntico ao campo de uma carga pontual. Agora vamos nos posicionar no interior da distribuição (\(r<R\)). Neste caso a carga interna \(Q_{i}\) à SG interna de raio \(r<R\) é
\begin{equation} Q_{i}=\rho_{0}\int\limits_{0}^{r}r^{2}dr\int\limits_{0}^{\pi}\sin\theta\,d\theta\int\limits_{0}^{2\pi}d\varphi=\rho_{0}\frac{4\pi}{3}r^{3}=Q\left(\frac{r}{R}\right)^{3}, \end{equation}
onde aproveitamos para trocar \(\rho_{0}\) em termos da carga total, usando o resultado em \((\ast)\). Sempre deixe seus resultados em termos da carga total, para facilitar comparações. Agora usaremos o Lema de Gauss, o fluxo através da superfície gaussiana
interna é proporcional à carga interna a esta superfície,
\begin{equation} \Phi=\oint\limits_{A}\vec{E}(\vec{r})\cdot d\vec{a}=E(r)\oint\limits_{A}da=4\pi r^{2}E(r)=4\pi C_{e}Q_{i}=4\pi C_{e}Q\left(\frac{r}{R}\right)^{3}\;\implies\; E(r)=C_{e}Q\frac{r}{R^{3}},\; r\leq R.\end{equation}
Vale ressaltar que este campo elétrico é linear na distância radial dentro da distribuição. Note também que os campos externo e interno têm o mesmo valor em \(r=R\) (superfície da distribuição). Potenciais. Podemos calcular os respectivos potenciais
escalares destes campos externo e interno. O potencial elétrico externo à distribuição é
\begin{equation} \phi_{e}(r)=-\int\vec{E}\cdot d\vec{r}=-C_{e}Q\int\frac{dr}{r^{2}}=C_{e}\frac{Q}{r}+c_{1},\; r\geq R, \end{equation}
onde \(c_{1}\) é uma constante arbitrária. O potencial elétrico interno à distribuição é
\begin{equation} \phi_{i}(r)=-\int\vec{E}\cdot d\vec{r}=-C_{e}Q\int\frac{rdr}{R^{3}}=-C_{e}Q\frac{r^{2}}{2R^{3}}+c_{2},\; r\leq R, \end{equation}
onde \(c_{2}\) é outra constante arbitrária. Podemos usar estas constantes arbitrárias para impor que estes potenciais tenham o mesmo valor na superfície da distribuição (em \(r=R\)),
\begin{equation} c_{2}-c_{1}=\frac{3}{2}\frac{C_{e}Q}{R}. \end{equation}
Uma escolha clássica é \(c_{1}=0\), potencial externo nulo no "infinito". Verifique estas afirmações. É altamente recomendável fazer diagramas (gráficos) destes potenciais e campos elétricos (por \(C_{e}Q\)).
Exercício 1. Aplique os procedimentos apresentados nestes exemplos para determinar o campo elétrico e o potencial elétrico correspondente (justifique a escolha da constante arbitrária) a uma
distância $r$ de um fio infinito de cargas elétricas com uma densidade linear constante, \(\lambda=\lambda_{0}\). Use a segunda figura na Tabela 2 como um corte transversal (considere um fio muito fino). Use coordenadas cilíndricas, com \(r\) como a
coordenada radial no plano perpendicular ao fio. Neste caso é melhor usar a densidade (ao invés da carga total) nas expressões resultantes (pelo fato do fio ser infinito). Resposta: \(\vec{E}(\vec{r})=E(r)\hat{r},\;
E(r)=2C_{e}\lambda_{0}/r,\) em coordenadas cilíndricas.
Exercício 2. Aplique os procedimentos apresentados nestes exemplos para determinar o campo elétrico e o potencial elétrico correspondente (justifique a escolha da constante arbitrária) a uma
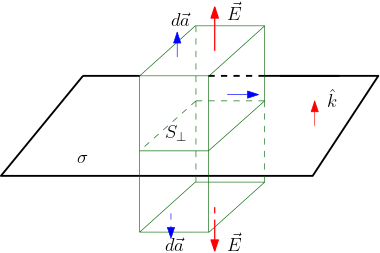
distância $z$ de um plano infinito de cargas elétricas com uma densidade superficial constante, \(\sigma=\sigma_{0}\). Use as informações apresentadas na quarta figura na Tabela 2. Use coordenadas cartesianas com o plano de cargas no plano \(xy\). Não
esqueça que um plano tem dois lados. Neste caso é melhor usar a densidade (ao invés da carga total) nas expressões resultantes (pelo fato do plano ser infinito). Resposta: \(\vec{E}(\vec{r})=E(z)\hat{k},\;
E(z)=2\pi C_{e}\sigma_{0},\) em coordenadas cartesianas.
"Lei" de Gauss. A "lei" de Gauss é consequência do teorema de Gauss,
\begin{equation} \int\limits_{A\supset V}\vec{E}\cdot d\vec{a} = \int\limits_{V}\vec{\nabla}\cdot\vec{E}\, dV, \end{equation}
o qual calcula o fluxo de um campo vetorial por uma integral de volume de seu divergente (veja os Apêndices). Usando o Lema de Gauss (consequência da lei de Coulomb), relacionamos o fluxo com a carga fonte,
\begin{equation} \int\limits_{A\supset V}\vec{E}\cdot d\vec{a} = 4\pi C_{e}\int\limits_{V}\rho dV= \int\limits_{V}\vec{\nabla}\cdot\vec{E}\, dV\;\implies\; \vec{\nabla}\cdot\vec{E}=4\pi C_{e}\rho. \end{equation}
Este resultado é conhecido também por "lei" de Gauss, mas é uma outra forma de enunciar a lei de Coulomb. A lei de Gauss diz que o divergente (fluxo por unidade de volume) do campo elétrico informa (localmente) a densidade de cargas que o criou. Maxwell
sintetizou este resultado em 1861, o qual denominaremos de primeira equação de Maxwell. O divergente funciona como um detector de fontes: é nulo na ausência delas e não-nulo na presença delas. Enquanto a lei de Coulomb é uma expressão global, válida
para todo o espaço, a lei de Gauss é local (válida numa determinada posição). Até aqui não enfatizamos uma possível dependência do campo (e do potencial) elétrico com o tempo, por conveniência (simplicidade). No entanto, a primeira equação de
Maxwell estabelecida aqui também é válida para campos dependentes do tempo.
É interessante escrever o campo elétrico em termos do potencial elétrico, \(\vec{E}=-\vec{\nabla}\phi\), e substituir na primeira equação de Maxwell,
\begin{equation} \vec{\nabla}\cdot\vec{E}= -\nabla^{2}\phi= 4\pi C_{e}\rho \;\implies\; \nabla^{2}\phi= -4\pi C_{e}\rho. \end{equation}
Este resultado é conhecido por equação de Poisson. O operador \(\nabla^{2}=\vec{\nabla}\cdot\vec{\nabla}\) é conhecido por laplaciano. A equação de Poisson reduz-se à equação de Laplace na ausência de cargas fonte (\(\rho=0\)).
Exercício 3. Verifique a lei de Gauss para casos discutidos nos exemplos e exercícios anteriores. Nos exemplos, o sistema de coordenadas é o esférico (as superfícies gaussianas são cascas esféricas).
No Exercício 1, o sistema de coordenadas é o cilíndrico (as superfícies gaussianas são cascas cilíndricas). No Exercício 2, o sistema de coordenadas pode ser tanto o cartesiano (sugerido), como o cilíndrico (as superfícies gaussianas podem ser cascas
de paralelepípedos ou cascas cilíndricas). Somente no Exemplo 2 o campo elétrico não é singular sobre as fontes.







