Programação
-
Expansão e aceleração: supernovas
Neste primeiro módulo vamos estudar de que modo as medidas de supernovas 1a foram determinantes para mostrar que o universo está se expandindo aceleradamente.
O primeiro passo é compreender como a métrica de FLRW pode ser usada para calcular distâncias, em particular a distância-luminosidade.
O segundo passo será utilizar essa base teórica em conjunto com os dados de uma compilação de supernovas, chamada Union2.1 . A documentação completa desses dados pode ser encontrada no site do Union2.1 na Univ. de Berkeley.
Você deve baixar esses dados, em particular: (1) os dados de redshift e módulo de distância, e (2) as matrizes de covariância (sem e com erros sistemáticos).
A sua primeira tarefa será escrever um código que calcule o chi^2 de um certo modelo cosmológico usando esses dados e as matrizes de covariância.
Aqui estão alguns dos passos necessários para completar essa tarefa (assumindo que você já baixou os dados e as matrizes de covariância):
1) Calcular numericamente a distância-luminosidade e o módulo de distância para um dado modelo cosmológico (que necessariamente deve permitir modelos com curvatura espacial); checar se essas distâncias estão corretas usando, por exemplo, a calculadora cosmológica em Java do Ned Wright (http://www.astro.ucla.edu/~wright/CosmoCalc.html)
2) Calcule a inversa da matriz de covariância (com erros sistemáticos); verifique se a inversão está numericamente estável (computando, p. ex., C^-1 . C ).
3) Calcule também a decomposição de Cholesky da matriz de covariância (C= L . L^tr).
4) Para um dado modelo teórico, calcule o vetor D = mu^t - mu^d, onde mu^t é o módulo de distância teórico (do seu modelo), e mu^d são os dados do módulo de distância. Em seguida, compute o chi^2 desse modelo, usando de dois métodos: (2a) usando a inversa da matriz de covariância, chi^2 = D . C^-1 . D; e (2b) usando a decomposição de Cholesky: chi^2 = Tr(s^2) , onde s é a solução do sistema linear L. s=D . Compare os dois resultados.
5) Agora, escolha um dos seus parâmetros teóricos (p. ex., \Omega_m) e deixe todos os outros parâmetros fixos. Faça um grid de valores para esse parâmetro e encontre a probabilidade desse parâmetro nesse grid, usando que p ~ exp( - 0.5 chi^2) . Estime o valor mais provável do seu parâmetro, assim como a dispersão em torno desse valor mais provável.
6) Agora adicione um outro parâmetro para ser variado (p. ex., w, a equação de estado da energia escura). Agora você deve fazer um grid em 2D, variando dois parâmetros. Guarde os valores de chi^2 para todos os pontos desse grid, e encontre a probabilidade conjunta dos dois parâmetros. Encontre os valores mais prováveis dos dois parâmetros e a região de confiança de 68% -- ou seja, encontre a região nesse espaço 2D na qual a probabilidade integrada acima de um certo valor, dentro dessa região, perfaz 0.68.
7) Agora faça o seguinte exercício: tome a probabilidade 2D acima e integre o segundo parâmetro (no caso, w). Ou seja, some sobre todas as linhas (ou colunas) correspondentes aos valores de w. O que vai sobrar é um vetor com as probabilidades para o primeiro parâmetro (no meu exemplo, \Omega_m), marginalizada sobre os valores de w. Compare essa curva com aquela obtida no item 5 acima. Você pode até fazer uma figura como esta:
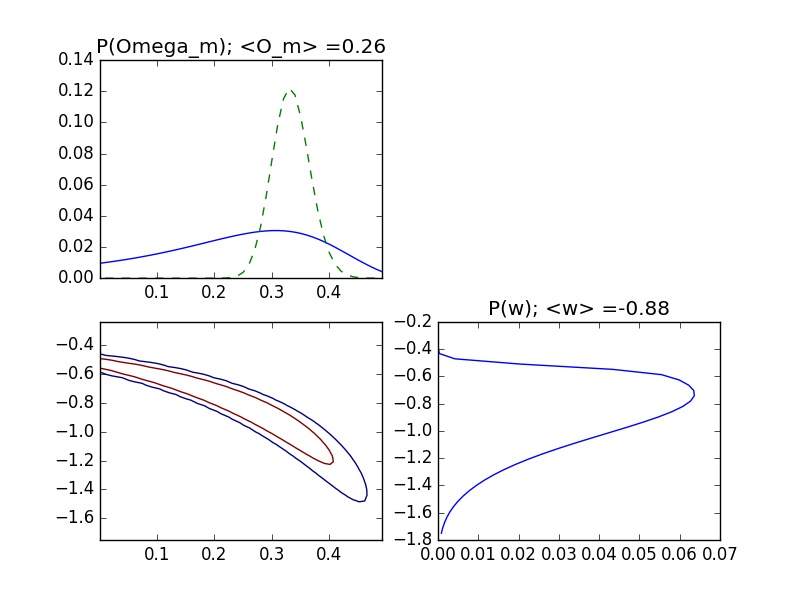
No plot de cima, a curva tracejada (verde) corresponde ao exercício 5, onde ficamos w=-1.
8) Finalmente, calcule a Matriz de Fisher para esses dois parâmetros, e calcule as incertezas correspondentes naquela aproximação. Compare com os resultados dessa aproximação com o item 6 acima.
Resultados dos alunos
Estou anexando arquivos com os resultados de quem me entregou até a data-limite (ontem, 6a-feira). Alguns resultados estão ótimos, está tudo lá. Porém, alguns de vocês parecem ter obtido resultados meio esquisitos, por favor chequem o que vocês fizeram, porque parece ter havido algum erro.