Física Básica I

Temos que entender o limite \( \)

do ponto de vista geométrico e torná-lo operacional. Note que estamos usando uma notação especial para representar este limite, denominada de derivada de $x(t)$ em relação a $t$. Importante: o símbolo $d/dt$ antes da primeira igualdade em $(\ast)$ deve ser entendido como um símbolo único sendo aplicado à função $x(t)$; já o símbolo $dx/dt$ antes da segunda igualdade em $(\ast)$ deve ser entendido como a razão entre duas quantidades infinitesimalmente pequenas, denominadas de diferenciais, o que nos faz lembrar do limite após a última igualdade em $(\ast)$. Note também na segunda igualdade em $(\ast)$ o uso do ponto para representar uma derivada temporal (e somente temporal). A seguir, vamos tornar operacional este conceito de derivada através de alguns exemplos.

Suponha que a equação horária no eixo $X$ seja uma constante, $x(t)=a$, isto é, repouso. Portanto a velocidade é nula. Então, levando a função constante $x(t)=a$ em $(\ast)$, teremos

pois o numerador já era nulo antes de executarmos o limite. Acabamos de aprender que a derivada de uma função constante é nula. Do ponto de vista geométrico, devemos perceber que uma função constante é uma reta paralela ao eixo $X$. Assim, qualquer função constante tem uma inclinação (ângulo formado com o eixo $X$) nula, cuja tangente (coeficiente angular) também é nula. Portanto, o coeficiente angular de uma reta paralela ao eixo $X$, $x(t)=a$, é numericamente igual à sua derivada em qualquer ponto, ou seja, nulo. Vejamos se esta relação entre derivada e tangente é mantida em um outro exemplo.

Considere agora uma equação horária linear no tempo, $x(t)=a+bt$, representando um movimento uniforme (velocidade constante). Então, como no caso anterior, levando a função $x(t)=a+bt$ em $(\ast)$, teremos

pois o numerador já era igual a $b$ (constante; independente do tempo) antes de executarmos o limite. Portanto, aprendemos que a derivada de uma função linear é igual ao seu coeficiente angular, confirmando assim nossa conjectura que a derivada calculada em um ponto $t$ é numericamente igual ao coeficiente angular da reta tangente à função $x(t)$ (no mesmo ponto $t$). Note que a reta tangente de uma reta coincide com a própria reta. Para confirmar esta conjectura sobre a interpretação geométrica da derivada, vejamos o próximo exemplo.

Considere agora uma função quadrática para a equação horária, $x(t)=a+bt+ct^{2}$, representando um movimento com aceleração constante. Então, levando esta função em $(\ast)$, teremos

pois o limite do termo $c\Delta t$ é obtido substituindo $\Delta t=0$. Uma regra para calcular limites: simplifique antes suas expressões. Voltaremos à interpretação geométrica em breve. A conjectura é: esta derivada nos permite calcular o coeficiente angular da reta tangente à curva $x(t)=a+bt+ct^{2}$ no ponto $(t,x(t))$.

Até aqui aprendemos que a derivada de um polin{\^{o}}mio $t^{n}$ obedece à regra $nt^{n-1}$. Também aprendemos que a derivada do produto de uma função $f(t)$ por uma constante $c$ obedece à regra $c\, df(t)/dt$, isto é, a constante pode sair para fora da derivada. Ao compararmos os resultados anteriores aprendemos que a derivada obedece a propriedade de linearidade, $d(f(t)+cg(t))/dt= df(t)/dt + c\, dg(t)/dt$. Em geral, as propriedades seguintes nos permitem calcular a derivada de qualquer função suave.

1. Derivada de uma constante: $\displaystyle \frac{d}{dt}a = 0$.
2. Derivada de uma potência: $\displaystyle \frac{d}{dt}t^{n} = nt^{n-1}$.
3. Linearidade: $\displaystyle \frac{d}{dt}\bigl(f(t)+bg(t)\bigr) = \frac{d}{dt}f(t) + b\frac{d}{dt}g(t)$.
4. Regra do produto: $\displaystyle \frac{d}{dt}\bigl(f(t)g(t)\bigr) = g(t)\frac{d}{dt}f(t) + f(t)\frac{d}{dt}g(t)$.
5. Regra da função composta: $\displaystyle \frac{d}{dt}f\bigl(g(t)\bigr) = \biggl[ \frac{d}{dg}f(g) \biggr]\, \frac{d}{dt}g(t)$.
   

De fato, cada uma destas propriedades serão estudadas em detalhes no curso de Cálculo. Em particular, as três últimas propriedades serão demonstradas adequadamente.

Para ilustramos como estas propriedades são utilizadas, precisamos aprender a calcular a derivada de algumas funções elementares, além de polinômios. Por exemplo, a função exponencial será muito importante para nossas discussões futuras. Vamos então calcular a derivada da função $x(t)=e^{\omega t}$ ($\omega$ constante), usando a definição $(\ast)$:

onde efetuamos a troca $\omega\Delta t\to \Delta s$. Note também que retiramos a expressão $\omega\, e^{\omega t}$ de dentro do limite, pois ela não depende de $\Delta t$. Nosso problema agora é calcular o limite apresentado no final desta expressão. Lembrando que a exponencial de zero é a unidade, então a exponencial de um número tendendo a zero deve ser um valor muito próximo da unidade (um pouquinho maior que a unidade se o argumento for positivo e um pouquinho menor que a unidade se o argumento for negativo). Assim, quando $\Delta s$ é muito pequeno, podemos escrever $e^{\Delta s}= 1+f(\Delta s)$, onde $f(\Delta s)$ é desconhecida, mas com duas propriedades: (i) $f(0)=0$ (caso contrário não teríamos $e^{0}=1$) e (ii) $f(\Delta s)=\Delta s$ é uma excelente aproximação para valores muito pequenos de $\Delta s$ (verifique isto numericamente com sua calculadora). Desta forma,

O curso de Cálculo apresentará uma demonstração muito mais elegante para este limite. Este resultado nos possibilita reescrever a nossa derivada como

Note que, no caso $\omega=1$, podemos dizer que a derivada da exponencial é ela mesma. A exponencial é a única função com esta propriedade (não esqueça).

Conhecendo a regra para derivar a exponencial, podemos calcular a derivada da função logarítmica. Por definição, dado $x(t)=\ln t$, temos $t=e^{x(t)}$. Derivando no tempo esta última expressão, temos $dt/dt=1$ no lado esquerdo e $de^{x(t)}/dt$ no lado direito, a qual é a derivada de uma função composta, pois $e^{x(t)}=y(x(t))$, com $y(x)=e^{x}$. Usando a regra da função composta, podemos escrever

Este resultado deve ser igualado à unidade (a derivada do lado esquerdo de $t=e^{x(t)}$). Assim,

Este é outro resultado muito útil é muito fácil de memorizar.

Para completar o quadro de derivadas de funções elementares que precisaremos, precisamos das derivadas das funções trigonométricas seno e cosseno. Novamente, vamos usar a definição $(\ast)$ de derivada e calcular a derivada da função seno,

Aqui é um bom momento para deixarmos um pouco de trabalho para o curso de Cálculo. Lá será provado, elegantemente, os limites fundamentais

Portanto, levando este dois resultados de volta na derivada da função seno,

Este é um resultado também único e muito fácil de ser memorizado: a derivado do seno é o cosseno. Lembrando que $\cos(t)=\sin(t+\pi/2)$, podemos obter a derivada do cosseno. Não podemos esquecer que $\sin(t+\pi/2)$ é uma função composta da forma $\sin(t+\pi/2)=f(g(t))$, com $f(g)=\sin(g)$ e $g(t)=t+\pi/2$. Como regra, toda função, por mais simples que seja, é uma função composta. Assim, a derivada do cosseno pode ser dada por

ou seja,

Não esqueça deste sinal negativo na derivada do cosseno (a função trigonométrica par). Note a troca de papeis entre as derivadas das funções trigonométricas seno e cosseno. Memorize as derivadas abaixo:

Vejamos mais alguns exemplos do uso das propriedades de derivadas. Por exemplo, suponha $y=\sin(2t^{2})$. Esta é uma função composta na forma $y=f(g(t))$, na qual $f(g)=\sin(g)$ e $g(t)=2t^{2}$. Assim, devemos usar a regra da função composta para efetuar sua derivada,

Vejamos este outro exemplo: $y=\cos(2t)e^{t^{2}}$. Desta vez temos um produto de duas funções (um cosseno vezes uma exponencial), na qual cada parcela é uma função composta. Assim, devemos usar primeiro a regra do produto e depois a regra da função composta,

Invente outros exemplos. Treine. Use computação algébrica para checar seus resultados. Pratique a vontade.

E a interpretação geométrica de derivada? Para fazermos esta interpretação corretamente, devemos resolver um outro problema (geométrico). Como determinar a equação da reta tangente em um dado ponto $t_{0}$ de uma dada curva $x(t)$? Veja a Figura 1. A única informação que temos é que esta reta tangente deve passar pelo ponto $(t_{0},x(t_{0}))$, e somente por este ponto numa vizinhança muito pequena em torno de $t_{0}$. No entanto, sabemos que precisaremos conhecer também o coeficiente angular desta reta tangente e que para isto precisaremos de um segundo ponto. Isto mesmo, o problema é que não temos este segundo ponto. Que fazer? A única atitude sensata é usar um outro ponto, digamos $x_{1}=x(t_{1})$, da curva $x(t)$, como indicado na Figura 1.

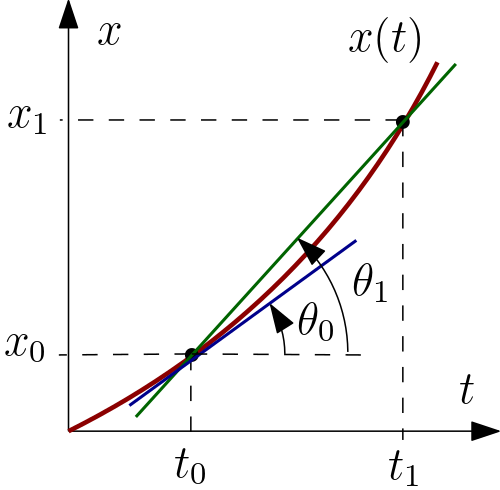
O coeficiente angular da reta secante passando pelos pontos $x_{0}=x(t_{0})$ e $x_{1}=x(t_{1})$ é

De fato, esta reta secante não é a mesma reta tangente que estamos procurando, mas se mantivermos $t_{0}$ fixo e aproximarmos $t_{1}$ de $t_{0}$, obteremos o coeficiente angular da reta tangente que procuramos,

Como este processo limite é o mesmo processo limite usado para definir a velocidade instantânea na Definição 1, podemos concluir que a derivada nos dá informação sobre retas tangentes de curvas: a derivada de uma função qualquer $f(t)$ é numericamente igual ao coeficiente angular da reta tangente passando por $(t,f(t))$. De fato, isto é uma solução (elegante e funcional) ao problema matemático de encontrar a reta tangente de uma curva plana (veja a Figura 1). Vejamos como isto funciona.

Suponha $x(t)=t^{2}/2$. A derivada desta função é $\dot{x}(t)=t$ (verifique). Suponha que estejamos interessados em determinar a reta tangente $\tau(t)=a+bt$ num determinado ponto $x_{0}=x(t_{0})$ da parábola $x(t)=t^{2}/2$, por exemplo em $t_{0}=2$, ou $x_{0}=2$. Acabamos de aprender que o coeficiente angular $b$ desta reta tangente pode ser calculado pela derivada $\dot{x}(t)$, avaliada no ponto em questão, ou seja, $b=\dot{x}(t_{0})$. Tomando $t_{0}=2$, o coeficiente angular da reta tangente passando neste ponto ($x_{0}=x(t_{0})=2$) é $b=\dot{x}(2)=2$. Assim, falta determinarmos o termo independente, $a$, da reta tangente $\tau(t)=a+2t$. Isto pode ser feito impondo que a reta tangente $\tau(t)$ e a parábola $x(t)$ tenham o mesmo valor em $t_{0}=2$ (é a definição da reta tangente: compartilhar um único ponto com a curva). Desta forma, de $\tau(2)=x(2)$ resulta a equação $a+4=2$, a qual implica em $a=-2$. Portanto, no ponto $(2,2)$, a parábola $x(t)=t^{2}/2$ tem uma tangente cuja equação é $\tau(t)=-2+2t$. Verifique isto desenhando simultaneamente a parábola $x(t)$ e sua reta tangente $\tau(t)$ (no ponto $t=2$) e veja que esta reta tangente toca (tangencia) a parábola apenas no ponto $t=2$.

Outra aplicação imediata desta interpretação geométrica: ela é muito útil para determinarmos os pontos extremos (máximos e mínimos) de funções, pois, nestes pontos de máximos e mínimos, a reta tangente é sempre horizontal (logo o seu coeficiente angular é nulo). Portanto, a derivada deve ser nula nos pontos extremos de uma função.