Apêndices
| Site: | Moodle USP: e-Disciplinas |
| Curso: | Física Básica I |
| Livro: | Apêndices |
| Impresso por: | Usuário visitante |
| Data: | quarta-feira, 3 jul. 2024, 10:16 |
Descrição
Materiais auxiliares.
1. Análise dimensional
Unidades de medida são importantes e indispensáveis. De forma geral, procuraremos expressar todas as nossas quantidades em unidades derivadas de quatro grandezas fundamentais: comprimento (L), tempo (T), massa (M) e carga elétrica (Q). Em processos
de medidas, estas grandezas são conhecidas também por dimensões. Em geral, falaremos da análise dimensional de uma determinada quantidade. Vários sistemas de medidas foram criados para expressar
a intensidade de cada uma destas quatro dimensões fundamentais. Usaremos com mais frequência o Sistema Internacional (SI ou MKS), onde comprimento é medido em metros (m), tempo em segundos
(s), massa em kilogramas (kg) e carga elétrica em Coulombs (C).
Existe um procedimento padrão para analisarmos as dimensões de uma determinada quantidade de interesse: uma equação com o lado esquerdo expressando a quantidade \(B\) a ser analisada, via a notação \([B]\), e um lado direito contendo apenas as operações
de multiplicação e potenciação envolvendo as dimensões L, T, M e Q. Vejamos alguns exemplos.
O vetor posição \(\vec{r}\) tem dimensão de comprimento (L). Escrevemos matematicamente esta informação como
\begin{equation}
[\vec{r}]=\text{L}.
\end{equation}
O vetor velocidade tem dimensões de comprimento por tempo,
\begin{equation}
[\vec{v}]=\biggl[\frac{d\vec{r}}{dt}\biggr] =
\frac{\text{L}}{\text{T}}= \text{LT}^{-1}.
\end{equation}
O vetor aceleração tem dimensões de comprimento por tempo ao quadrado,
\begin{equation}
[\vec{a}]=\biggl[\frac{d^{2}\vec{r}}{dt^{2}}\biggr] =
\frac{\text{L}}{\text{T}^{2}}=\text{LT}^{-2}.
\end{equation}
As dimensões do momentum linear são
\begin{equation}
[\vec{p}]=\bigl[m\vec{v}\bigr] = \frac{\text{ML}}{\text{T}}=
\text{MLT}^{-1}.
\end{equation}
Seguindo estes exemplos, a análise dimensional do vetor força na segunda lei de Newton (massa constante) nos fornece
\begin{equation}
[\vec{F}]=\bigl[m\vec{a}\bigr] = \frac{\text{ML}}{\text{T}^{2}}=
\text{MLT}^{-2} \text{(Newton)}.
\end{equation}
Newton é a unidade de força no sistema MKS.
Quais são as dimensões da constante \(C_{e}\) aparecendo na expressão para a força elétrica (lei de Coulomb)
\begin{equation}
\label{eq:Coulomb2}
\vec{F}_{e}=C_{e}\frac{Qq}{r^{2}}\hat{r}
\end{equation}
entre duas cargas elétricas \(Q\) e \(q\) separadas pela distância \(r\)? Seguindo o modelo anterior, temos
\begin{equation}
\label{eq:aCe}
[C_{e}]=\text{NL}^{2}\text{Q}^{-2}=\text{ML}^{3}\text{T}^{-2}\text{Q}^{-2}.
\end{equation}
Por completeza, devemos mencionar que cargas magnéticas nunca foram observadas. No entanto quando dois fios conduzindo correntes elétricas \(I_{1}\) e \(I_{2}\) estão a uma distância \(\rho\), podemos medir uma força por unidade de comprimento entre eles,
\begin{equation}
\label{eq:BiotSavat}
\vec{f}_{m}=2C_{m}\frac{I_{1}I_{2}}{\rho}\hat{\rho}.
\end{equation}
Esta força é conhecida como lei de Biot-Savat. Usando a definição de corrente, carga por tempo, temos
\begin{equation}
\label{eq:aI}
[I]=\biggl[\frac{dQ}{dt}\biggr] = \text{QT}^{-1}.
\end{equation}
Assim, as dimensões da constante \(C_{m}\) são
\begin{equation}
\label{eq:aCm}
[C_{m}]=\text{NT}^{2}\text{Q}^{-2}=\text{MLQ}^{-2}.
\end{equation}
Podemos notar também então que a razão \(C_{e}/C_{m}\) tem a mesma dimensão de velocidade ao quadrado. De fato, Maxwell mostrou que no vácuo, a velocidade da luz (onda eletromagnética) é
\begin{equation}
\label{eq:veluz}
c=\sqrt{\frac{C_{e}}{C_{m}}}.
\end{equation}
Os valores destas constantes (no vácuo) são: \(C_{e}=8.987\,551\,788\times 10^{9}\) N\(\cdot\)m\(^{2}\)/C\(^{2}\) e \(C_{m}=10^{-7}\) N\(\cdot\)s\(^{2}\)/C\(^{2}\). Portanto, medindo as constantes \(C_{e}\) e \(C_{m}\) podemos calcular a velocidade
da luz. Este resultado está entre os mais surpreendentes acerca da nossa natureza. As surpresas não param aqui, há ainda um fato ainda mais marcante sobre o comportamento da luz: ela é um limite superior para a velocidade de qualquer quantidade
em movimento. No presente tempo, conseguimos dar uma velocidade próxima à da luz (98%) apenas para partículas sub-atômicas como o elétron.
A força de Lorentz,
\begin{equation}
\label{eq:db}
\vec{F} = q\,\vec{v}\times\vec{B},
\end{equation}
produzida por uma carga \(q\) em movimento com uma velocidade \(\vec{v}\) em um campo magnético \(\vec{B}\), é responsável por trajetórias helicoidais. As dimensões do campo magnético \(\vec{B}\) são
\begin{equation}
\label{eq:db2}
[\vec{B}]=\biggl[\frac{||\vec{F}||}{q||\vec{v}||}\biggr] =
\text{MQ}^{-1}\text{T}^{-1} \text{(Tesla)}.
\end{equation}
2. Derivadas
Temos que entender o limite \( \)
do ponto de vista geométrico e torná-lo operacional. Note que estamos usando uma notação especial para representar este limite, denominada de derivada de $x(t)$ em relação a $t$. Importante: o símbolo
$d/dt$ antes da primeira igualdade em $(\ast)$ deve ser entendido como um símbolo único sendo aplicado à função $x(t)$; já o símbolo $dx/dt$ antes da segunda igualdade em $(\ast)$ deve ser entendido como a razão entre duas quantidades infinitesimalmente
pequenas, denominadas de diferenciais, o que nos faz lembrar do limite após a última igualdade em $(\ast)$. Note também na segunda igualdade em $(\ast)$ o uso do ponto para representar uma derivada temporal (e somente temporal). A seguir, vamos tornar
operacional este conceito de derivada através de alguns exemplos.
Suponha que a equação horária no eixo $X$ seja uma constante, $x(t)=a$, isto é, repouso. Portanto a velocidade é nula. Então, levando a função constante $x(t)=a$ em $(\ast)$, teremos
\begin{equation} \label{eq:limCte} \frac{d}{dt} x(t) = \lim_{\Delta t\to 0} \frac{x(t+\Delta t)-x(t)}{\Delta t} = \lim_{\Delta t\to 0} \frac{a-a}{\Delta t} = \lim_{\Delta t\to 0} 0 = 0, \end{equation}
pois o numerador já era nulo antes de executarmos o limite. Acabamos de aprender que a derivada de uma função constante é nula. Do ponto de vista geométrico, devemos perceber que uma função constante é uma reta paralela ao eixo $X$. Assim, qualquer função
constante tem uma inclinação (ângulo formado com o eixo $X$) nula, cuja tangente (coeficiente angular) também é nula. Portanto, o coeficiente angular de uma reta paralela ao eixo $X$, $x(t)=a$, é numericamente igual à sua derivada em qualquer ponto,
ou seja, nulo. Vejamos se esta relação entre derivada e tangente é mantida em um outro exemplo.
Considere agora uma equação horária linear no tempo, $x(t)=a+bt$, representando um movimento uniforme (velocidade constante). Então, como no caso anterior, levando a função $x(t)=a+bt$ em $(\ast)$, teremos
pois o numerador já era igual a $b$ (constante; independente do tempo) antes de executarmos o limite. Portanto, aprendemos que a derivada de uma função linear é igual ao seu coeficiente angular, confirmando assim nossa conjectura que a derivada calculada
em um ponto $t$ é numericamente igual ao coeficiente angular da reta tangente à função $x(t)$ (no mesmo ponto $t$). Note que a reta tangente de uma reta coincide com a própria reta. Para confirmar esta conjectura sobre a interpretação geométrica da
derivada, vejamos o próximo exemplo.
Considere agora uma função quadrática para a equação horária, $x(t)=a+bt+ct^{2}$, representando um movimento com aceleração constante. Então, levando esta função em $(\ast)$, teremos
pois o limite do termo $c\Delta t$ é obtido substituindo $\Delta t=0$. Uma regra para calcular limites: simplifique antes suas expressões. Voltaremos à interpretação geométrica em breve. A conjectura é: esta derivada nos permite calcular o coeficiente
angular da reta tangente à curva $x(t)=a+bt+ct^{2}$ no ponto $(t,x(t))$.
Até aqui aprendemos que a derivada de um polin{\^{o}}mio $t^{n}$ obedece à regra $nt^{n-1}$. Também aprendemos que a derivada do produto de uma função $f(t)$ por uma constante $c$ obedece à regra $c\, df(t)/dt$, isto é, a constante pode sair para fora
da derivada. Ao compararmos os resultados anteriores aprendemos que a derivada obedece a propriedade de linearidade, $d(f(t)+cg(t))/dt= df(t)/dt + c\, dg(t)/dt$. Em geral, as propriedades seguintes nos permitem calcular a derivada de qualquer função
suave.
- Derivada de uma constante: $\displaystyle \frac{d}{dt}a = 0$.
- Derivada de uma potência: $\displaystyle \frac{d}{dt}t^{n} = nt^{n-1}$.
- Linearidade: $\displaystyle \frac{d}{dt}\bigl(f(t)+bg(t)\bigr) = \frac{d}{dt}f(t) + b\frac{d}{dt}g(t)$.
- Regra do produto: $\displaystyle \frac{d}{dt}\bigl(f(t)g(t)\bigr) = g(t)\frac{d}{dt}f(t) + f(t)\frac{d}{dt}g(t)$.
- Regra da função composta: $\displaystyle \frac{d}{dt}f\bigl(g(t)\bigr) = \biggl[ \frac{d}{dg}f(g) \biggr]\, \frac{d}{dt}g(t)$.
De fato, cada uma destas propriedades serão estudadas em detalhes no curso de Cálculo. Em particular, as três últimas propriedades serão demonstradas adequadamente.
Para ilustramos como estas propriedades são utilizadas, precisamos aprender a calcular a derivada de algumas funções elementares, além de polinômios. Por exemplo, a função exponencial será muito importante para nossas discussões futuras. Vamos então calcular
a derivada da função $x(t)=e^{\omega t}$ ($\omega$ constante), usando a definição $(\ast)$:
onde efetuamos a troca $\omega\Delta t\to \Delta s$. Note também que retiramos a expressão $\omega\, e^{\omega t}$ de dentro do limite, pois ela não depende de $\Delta t$. Nosso problema agora é calcular o limite apresentado no final desta expressão.
Lembrando que a exponencial de zero é a unidade, então a exponencial de um número tendendo a zero deve ser um valor muito próximo da unidade (um pouquinho maior que a unidade se o argumento for positivo e um pouquinho menor que a unidade se o argumento
for negativo). Assim, quando $\Delta s$ é muito pequeno, podemos escrever $e^{\Delta s}= 1+f(\Delta s)$, onde $f(\Delta s)$ é desconhecida, mas com duas propriedades: (i) $f(0)=0$ (caso contrário não teríamos $e^{0}=1$) e (ii) $f(\Delta s)=\Delta s$
é uma excelente aproximação para valores muito pequenos de $\Delta s$ (verifique isto numericamente com sua calculadora). Desta forma,
O curso de Cálculo apresentará uma demonstração muito mais elegante para este limite. Este resultado nos possibilita reescrever a nossa derivada como
Note que, no caso $\omega=1$, podemos dizer que a derivada da exponencial é ela mesma. A exponencial é a única função com esta propriedade (não esqueça).
Conhecendo a regra para derivar a exponencial, podemos calcular a derivada da função logarítmica. Por definição, dado $x(t)=\ln t$, temos $t=e^{x(t)}$. Derivando no tempo esta última expressão, temos $dt/dt=1$ no lado esquerdo e $de^{x(t)}/dt$ no lado
direito, a qual é a derivada de uma função composta, pois $e^{x(t)}=y(x(t))$, com $y(x)=e^{x}$. Usando a regra da função composta, podemos escrever
Este resultado deve ser igualado à unidade (a derivada do lado esquerdo de $t=e^{x(t)}$). Assim,
Este é outro resultado muito útil é muito fácil de memorizar.
Para completar o quadro de derivadas de funções elementares que precisaremos, precisamos das derivadas das funções trigonométricas seno e cosseno. Novamente, vamos usar a definição $(\ast)$ de derivada e calcular a derivada da função seno,
Aqui é um bom momento para deixarmos um pouco de trabalho para o curso de Cálculo. Lá será provado, elegantemente, os limites fundamentais
Portanto, levando este dois resultados de volta na derivada da função seno,
Este é um resultado também único e muito fácil de ser memorizado: a derivado do seno é o cosseno. Lembrando que $\cos(t)=\sin(t+\pi/2)$, podemos obter a derivada do cosseno. Não podemos esquecer que $\sin(t+\pi/2)$ é uma função composta da forma $\sin(t+\pi/2)=f(g(t))$,
com $f(g)=\sin(g)$ e $g(t)=t+\pi/2$. Como regra, toda função, por mais simples que seja, é uma função composta. Assim, a derivada do cosseno pode ser dada por
ou seja,
Não esqueça deste sinal negativo na derivada do cosseno (a função trigonométrica par). Note a troca de papeis entre as derivadas das funções trigonométricas seno e cosseno. Memorize as derivadas abaixo:
Vejamos mais alguns exemplos do uso das propriedades de derivadas. Por exemplo, suponha $y=\sin(2t^{2})$. Esta é uma função composta na forma $y=f(g(t))$, na qual $f(g)=\sin(g)$ e $g(t)=2t^{2}$. Assim, devemos usar a regra da função composta para efetuar
sua derivada,
Vejamos este outro exemplo: $y=\cos(2t)e^{t^{2}}$. Desta vez temos um produto de duas funções (um cosseno vezes uma exponencial), na qual cada parcela é uma função composta. Assim, devemos usar primeiro a regra do produto e depois a regra da função composta,
Invente outros exemplos. Treine. Use computação algébrica para checar seus resultados. Pratique a vontade.
E a interpretação geométrica de derivada? Para fazermos esta interpretação corretamente, devemos resolver um outro problema (geométrico). Como determinar a equação da reta tangente em um dado ponto
$t_{0}$ de uma dada curva $x(t)$? Veja a Figura 1. A única informação que temos é que esta reta tangente deve passar pelo ponto $(t_{0},x(t_{0}))$, e somente por este ponto numa vizinhança muito pequena em torno de $t_{0}$. No entanto, sabemos que precisaremos
conhecer também o coeficiente angular desta reta tangente e que para isto precisaremos de um segundo ponto. Isto mesmo, o problema é que não temos este segundo ponto. Que fazer? A única atitude sensata é usar um outro ponto, digamos $x_{1}=x(t_{1})$,
da curva $x(t)$, como indicado na Figura 1.
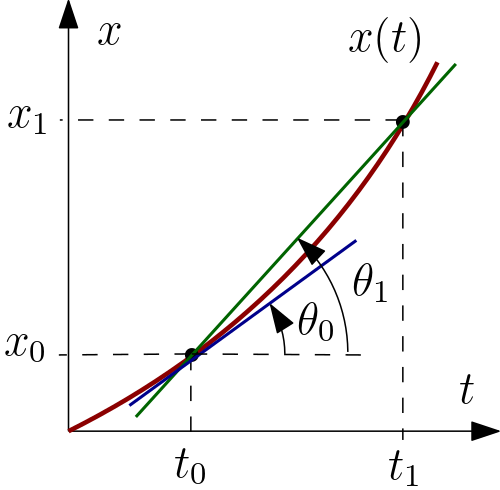
O coeficiente angular da reta secante passando pelos pontos $x_{0}=x(t_{0})$ e $x_{1}=x(t_{1})$ é
De fato, esta reta secante não é a mesma reta tangente que estamos procurando, mas se mantivermos $t_{0}$ fixo e aproximarmos $t_{1}$ de $t_{0}$, obteremos o coeficiente angular da reta tangente que procuramos,
Como este processo limite é o mesmo processo limite usado para definir a velocidade instantânea na Definição 1, podemos concluir que a derivada nos dá informação sobre retas tangentes de curvas: a derivada de uma função qualquer $f(t)$ é numericamente igual ao coeficiente angular da reta tangente passando por $(t,f(t))$.
De fato, isto é uma solução (elegante e funcional) ao problema matemático de encontrar a reta tangente de uma curva plana (veja a Figura 1). Vejamos como isto funciona.
Suponha $x(t)=t^{2}/2$. A derivada desta função é $\dot{x}(t)=t$ (verifique). Suponha que estejamos interessados em determinar a reta tangente $\tau(t)=a+bt$ num determinado ponto $x_{0}=x(t_{0})$ da parábola $x(t)=t^{2}/2$, por exemplo em $t_{0}=2$, ou $x_{0}=2$. Acabamos de aprender que o coeficiente angular $b$ desta reta tangente pode ser calculado pela derivada $\dot{x}(t)$, avaliada no ponto em questão, ou seja, $b=\dot{x}(t_{0})$. Tomando $t_{0}=2$, o coeficiente angular da reta tangente passando neste ponto ($x_{0}=x(t_{0})=2$) é $b=\dot{x}(2)=2$. Assim, falta determinarmos o termo independente, $a$, da reta tangente $\tau(t)=a+2t$. Isto pode ser feito impondo que a reta tangente $\tau(t)$ e a parábola $x(t)$ tenham o mesmo valor em $t_{0}=2$ (é a definição da reta tangente: compartilhar um único ponto com a curva). Desta forma, de $\tau(2)=x(2)$ resulta a equação $a+4=2$, a qual implica em $a=-2$. Portanto, no ponto $(2,2)$, a parábola $x(t)=t^{2}/2$ tem uma tangente cuja equação é $\tau(t)=-2+2t$. Verifique isto desenhando simultaneamente a parábola $x(t)$ e sua reta tangente $\tau(t)$ (no ponto $t=2$) e veja que esta reta tangente toca (tangencia) a parábola apenas no ponto $t=2$.
Outra aplicação imediata desta interpretação geométrica: ela é muito útil para determinarmos os pontos extremos (máximos e mínimos) de funções, pois, nestes pontos de máximos e mínimos, a reta tangente é sempre horizontal (logo o seu coeficiente angular é nulo). Portanto, a derivada deve ser nula nos pontos extremos de uma função.
3. Sistemas de coordenadas
em breve...