Anterior
Próximo

4. Distância percorrida (Integral)

4.1. Estratégia

A Figura 1 ilustra a estratégia para construirmos uma ferramenta algébrica para calcular a distância percorrida (ou comprimento) \(\Delta S\) sobre uma dada trajetória $\gamma(t)$, com curvatura e torção, entre os pontos inicial $t_{i}=t_{0}$ e final $t_{f}=t_{N}$. Estamos identificando pontos na trajetória por valores do parâmetro $t$ (tempo). Naturalmente, a distância percorrida $\Delta S$ é maior que a distância entre os pontos inicial e final dada pelo comprimento $\|\vec{R}\|$ do vetor diferença entre estes dois pontos, $\vec{R}=\vec{r}_{f}-\vec{r}_{i}$.

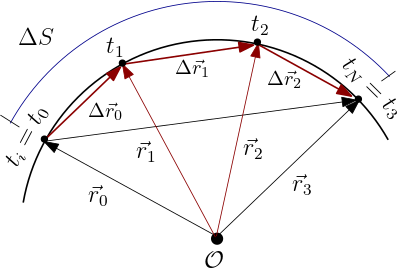
Figura 1. Estratégia para calcular o comprimento $\Delta S$ na trajetória $\gamma$.

No entanto, apesar do fato $\Delta S> \|\vec{r}_{f}-\vec{r}_{i}\|$, está aí a semente de uma ideia frutífera: inserir pontos intermediários como $t_{1}$ e $t_{2}$ mostrados na Figura 1, por exemplo, e observar que a soma dos comprimentos das diferenças sucessivas entre os vetores posição em $t_{0}$, $t_{1}$, $t_{2}$ e $t_{N}$ ($N=3$), é uma aproximação muito melhor para a distância percorrida,

\begin{equation} \label{eq:DS1} \Delta S\approx \sum\limits_{j=0}^{N=3}\|\Delta\vec{r}_{j}\|, \end{equation}

onde

\begin{equation} \label{eq:DR} \Delta\vec{r}_{j}=\vec{r}_{j+1}-\vec{r}_{j}. \end{equation}

Note que estamos trocando a soma nos arcos (pequenos trechos na trajetória) pela soma nas cordas (comprimentos das diferenças vetoriais).

Desta forma, a soma dos comprimentos das diferenças sucessivas entre os vetores posição de $N$ pontos sobre a trajetória é uma aproximação inferior para a distância percorrida. No limite $N\to\infty$ devemos obter uma igualdade,

\begin{equation} \label{eq:DS2} \lim_{N\to\infty}\sum\limits_{j=0}^{N}\|\Delta\vec{r}_{j}\|\to \Delta S. \end{equation}

Como tornar este limite operacional? O que ganhamos trocando a soma nos arcos pela soma nas cordas? Ganhamos muito! O comprimento $\|\Delta\vec{r}_{j}\|$ de cada corda pode ser expresso em termos da velocidade (média),

\begin{equation} \label{eq:comp1} \|\Delta\vec{r}_{i}\| = \sqrt{\Delta\vec{r}_{i}\cdot\Delta\vec{r}_{i}} = \sqrt{\frac{\Delta\vec{r}_{i}}{\Delta t_{i}}\cdot \frac{\Delta\vec{r}_{i}}{\Delta t_{i}}}\, \Delta t_{i} = \sqrt{\vec{v}_{i}\cdot\vec{v}_{i}}\, \Delta t_{i} = \|\vec{v}_{i}\|\, \Delta t_{i} = v_{i}\, \Delta t_{i}. \end{equation}

Note que $v_{i}=v(t_{i})$ é na verdade uma velocidade média, mas será a velocidade instantânea no limite $\Delta t\to 0$. Lembre-se que $N\to\infty$ é equivalente a $\Delta t\to 0$. Assim, a distância percorrida pode ser calculada pelo limite

\begin{equation} \label{eq:DS3} \Delta S=\lim_{N\to\infty}\sum\limits_{j=0}^{N}v_{j}\, \Delta t_{j}. \end{equation}

A nossa capacidade em executar estas somas infinitas é simplesmente incrível.



Anterior
Próximo