Cinemática
| Site: | Moodle USP: e-Disciplinas |
| Curso: | Física Básica I |
| Livro: | Cinemática |
| Impresso por: | Usuário visitante |
| Data: | quarta-feira, 3 jul. 2024, 08:34 |
Descrição
Cinemática: elementos geométricos e analíticos necessários à descrição do movimento, sem se preocupar com suas causas. Curvas espaciais descreverão trajetórias. Trajetórias serão descritas em sistemas de coordenadas. Movimento será descrito pelos vetores posição,
velocidade e aceleração. Taxas de variação serão descritas por derivadas. Espaço percorrido será descrito por integrais.
1. Introdução
Este curso usa as leis da Mecânica newtoniana para ampliar a familiaridade com o método científico, da mesma forma que usamos uma academia de ginástica. Portanto, participação ativa é fundamental. Não há qualquer benefício em observar passivamente os aparelhos numa sala de ginástica. As ferramentas matemáticas necessárias serão construídas e/ou reconstruídas, bem como procedimentos científicos, na medida da necessidade. Conhecimentos de Cálculo (derivadas e integrais), Geometria (pontos, curvas, vetores e sistemas de coordenadas) e Computação (simulação, visualização e computação algébrica) serão colocados juntos na descrição de alguns sistemas mecânicos via o conceito de modelo científico.
Estudaremos em Cinemática os conceitos de posição, velocidade, aceleração e trajetórias, sem nos preocuparmos com as suas causas. Procuraremos construir ferramentas matemáticas adequadas a uma descrição elegante e prática destas grandezas físicas.
Em geral, um objeto qualquer move-se em um determinado espaço, geralmente o espaço euclidiano tridimensional. Portanto, precisaremos construir uma forma efetiva de representar posição, velocidade, aceleração e trajetória deste objeto em cada instante de tempo neste espaço. Para efetuarmos esta representação, precisaremos de ferramentas matemáticas. Precisaremos de pontos para localizar nossos objetos físicos e de curvas espaciais para representar suas trajetórias. Precisaremos de vetores para representar posição, velocidade, aceleração e forças. Precisaremos de um sistema de coordenadas para descrever pontos, vetores e trajetórias. Precisaremos de produtos escalares e vetoriais para extrairmos informações mensuráveis de vetores, bem como construir novos vetores. Também precisaremos de ferramentas do Cálculo (derivadas e integrais) para expressar taxas de variação (no tempo) e espaço percorrido. Computação é indispensável para simularmos e visualizarmos movimentos em sistemas mecânicos, além de realizar operações algébricas tediosas de serem realizadas manualmente (computação algébrica).
No decorrer de nossas atividades desenvolveremos também a (incrível) capacidade de construir modelos, onde sistemas mecânicos são descritos matematicamente, possibilitando e facilitando a descoberta de informações novas (previsões). Um bom modelo tem uma forma circular (perfeita). Observações sobre um sistema leva a uma descrição matemática que leva a informações novas (dificilmente descobertas pela experimentação direta). Naturalmente, o modus operandi trabalhado nesta construção de modelos pode ser aplicado a qualquer área da ciência.
2. Geometria
O que é o espaço? Pode parecer inacreditável, mas ainda não dispomos de uma resposta concreta a esta pergunta e, talvez, nunca venhamos tê-la. No entanto, veremos que, mesmo desprovidos de uma definição, seremos capazes de usar o espaço de forma operacional. Encontraremos outras duas situações análogas envolvendo os conceitos de tempo e massa. Esta capacidade de operar com conceitos desprovidos de uma definição única é, sem dúvidas, uma das grandes conquistas humanas. A própria Geometria é um exemplo brilhante desta superação.
Precisaremos de um sistema de coordenadas para descrever pontos, curvas e vetores. Assim, seremos capazes de descrever um movimento real por expressões matemáticas. Descartes transformou objetos geométricos em expressões matemáticas (analíticas, algébricas), criando a Geometria Analítica. De forma similar, iremos construir modelos matemáticos que substituirão sistemas mecânicos reais. Geometria sempre foi, e continua sendo, uma grande fonte de inspiração.
Notas importantes. Para serem memorizadas.
- O produto escalar é um número real e, geometricamente, está associado à projeção de um vetor sobre o outro (Teoremas 1 e 2).
- O produto vetorial fornece um novo vetor (na verdade, um pseudo-vetor) cuja norma (módulo) é numericamente igual à área do paralelogramo subentendido pelos dois vetores que foram usados no produto vetorial (Teoremas 3 e 4).
- O produto misto é invariante por permutações circulares (cíclicas) de seus vetores (Teorema 5).
- A representação paramétrica é a forma mais eficiente de representar analiticamente uma curva espacial (trajetória).
2.1. Euclidiana
Vamos admitir a "existência'' de um espaço caracterizado pelas seguintes qualidades:
- a soma dos espaços das partes é igual ao espaço do todo contendo estas partes;
- o espaço é desprovido de matéria e, portanto, desprovido de qualquer propriedade que possa influenciar no movimento dos corpos;
- o espaço é homogêneo, isto é, qualquer posição ao longo de uma determinada direção é sempre igual às demais;
- o espaço é isotrópico, isto é, estando em uma posição fixa, todas as direções são idênticas;
- o espaço apresenta três dimensões independentes (por exemplo, largura, profundidade e altura) e é infinito.
Estas propriedades tornam operacional o conceito de espaço euclidiano, uma homenagem ao matemático grego Euclides que viveu no Séc. III a.C., considerado o fundador da geometria plana, foi estabelecido
somente a partir do Séc. XIV.
Tendo estabelecido estas propriedades, podemos afirmar que objetos podem ser localizados neste espaço através de coordenadas, medidas em relação a alguma posição fixa, previamente escolhida, a qual chamaremos de referencial.
Note, portanto, que coordenadas são medidas relativas de distância.
Usaremos aqui as noções de ponto como sendo um objeto adimensional, de curva como sendo um objeto unidimensional (tendo apenas comprimento, como retas, parábolas, circunferências, elipses, espirais, etc.) e de superfície como sendo um objeto bidimensional (tendo apenas área, como planos, cascas esféricas e cilíndricas, etc.). Também utilizaremos a noção de vetor como sendo uma flecha (segmento orientado) tendo comprimento, direção e sentido. Portanto, vetores são objetos que necessitam de três informações para serem especificados. Objetos que precisam de apenas uma informação para serem especificados, como os números reais, são denominados de escalares. Também assumiremos que o teorema de Pitágoras para triângulos retângulos seja conhecido (a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa).
Também é importante mencionar que espaço e tempo são conceitos distintos na mecânica newtoniana, ou seja, relógios sincronizados podem ser colocados simultaneamente em qualquer posição neste espaço que estamos considerando. Desta forma, trabalharemos
com a noção de tempo absoluto, ou seja, relógios sincronizados sempre marcarão os mesmos intervalos de tempo em qualquer posição do espaço.
2.2. Referencial
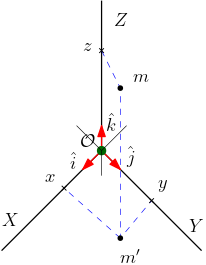
Muito bem, tendo estabelecido as principais propriedades do espaço euclidiano, precisamos construir um referencial para localizar pontos e curvas (restringindo aos objetos geométricos que nos interessa mais). Uma vez que estaremos considerando o espaço euclidiano tridimensional, o referencial mais simples deverá apresentar um ponto fixo (a origem) pelo qual passam três retas mutuamente ortogonais e indicar um sentido positivo em cada uma delas (eixos orientados). Denominemos de \(\mathcal{O}\) a origem, de $X$, $Y$ e $Z$ os eixos mutuamente perpendiculares e de $\hat{i}$, $\hat{j}$ e $\hat{k}$ os segmentos orientados de comprimentos unitários em cada eixo. Esses segmentos orientados unitários são denominados de versores. Um ponto $m$ será "localizado" neste referencial pelo seguinte procedimento geométrico:
- trace uma reta paralela ao eixo $Z$, passando por $m$, até interceptar o plano $XY$ em $m'$;
- trace uma reta paralela ao eixo $Y$, passando por $m'$, até interceptar o eixo $X$ em $x$;
- trace uma reta paralela ao eixo $X$, passando por $m'$, até interceptar o eixo $Y$ em $y$;
- trace uma reta paralela ao plano $XY$, passando por $m$, até interceptar o eixo $Z$ em $z$;
- as projeções $(x,y,z)$ são as coordenadas do ponto $m$.
A Figura 1 ilustra o ponto $m$, com coordenadas $m=(x,y,z)$, representado em um referencial com eixos $X$, $Y$ e $Z$ mutuamente perpendiculares (ortogonais), conhecido como sistema de coordenadas cartesiano, ou simplesmente sistema ortonormal de coordenadas, introduzido por René Descartes no Séc. XVII. Em geral usamos a origem para nomear um sistema de coordenadas. Neste caso, dizemos "o referencial (ortonormal) $\mathcal{O}$".
E se os eixos do referencial não forem ortogonais (perpendiculares)? Neste caso há mais de uma forma "canônica" de construirmos as coordenadas de um ponto. Você questionou o uso de retas paralelas (aos eixos) no procedimento geométrico usado para construir as coordenadas no referencial ortonormal? Por que não retas com uma outra inclinação? Para reduzir ao mínimo o número de possibilidades, o bom senso pede para usarmos retas paralelas ou perpendiculares aos eixos. A Figura 2 ilustra o uso de retas paralelas e perpendiculares aos eixos, resultando em projeções diferentes $(x,y)$ e $(\bar{x},\bar{y})$. Embora estas projeções distintas possam ser relacionadas, deixaremos este exercício para outra oportunidade.
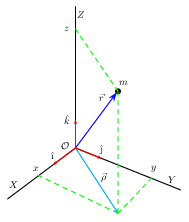
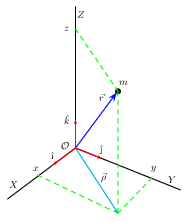
Como podemos calcular a distância entre dois pontos usando suas coordenadas? A distância entre dois pontos é o comprimento do segmento de reta que os une. Por exemplo, o segmento de reta que une a origem $\mathcal{O}=(0,0,0)$ e o ponto $m=(x,y,z)$ na Figura 3 tem um comprimento igual a $\sqrt{x^{2}+y^{2}+z^{2}}$. Este resultado pode ser obtido aplicando o teorema de Pitágoras duas vezes (faça o Exercício 1). Este exemplo nos ensina que em geral a distância $d(A,B)$ entre dois pontos quaisquer $A=(x_{a},y_{a},z_{a})$ e $B=(x_{b},y_{b},z_{b})$ é
\begin{equation} d(A,B) =\sqrt{(x_{b}-x_{a})^{2}+(y_{b}-y_{a})^{2}+(z_{b}-z_{a})^{2}}. \end{equation}Esse resultado será válido mesmo se esses dois pontos estiverem infinitesimalmente próximos. Há outra utilidade para esta distância entre dois pontos num espaço euclidiano. Denominemos por vetor um segmento de reta com uma orientação (segmento orientado, flecha). Como todo segmento orientado inicia em um ponto, digamos $A=(x_{a},y_{a},z_{a})$, e termina em outro, digamos $B=(x_{b},y_{b},z_{b})$, então o comprimento (ou norma) $||\vec{AB}||$ do vetor $\vec{AB}$ é
\begin{equation} ||\vec{AB}|| =\sqrt{(x_{b}-x_{a})^{2}+(y_{b}-y_{a})^{2}+(z_{b}-z_{a})^{2}}. \end{equation}| Figura 1 |
Figura 2 |
Figura 3 |
|---|---|---|
 |
 |
 |
Exercício 1. Use o teorema de Pitágoras para determinar o comprimento do vetor $\vec{\rho}$ no plano $XY$ na Figura 3 em termos das coordenadas $x$ e $y$. Use régua e papel e lápis e
desenhe um triângulo retângulo formado com os catetos $x=4$ cm e $y=3$ cm. Verifique (experimentalmente) com sua régua que o comprimento da hipotenusa é muito próximo do valor calculado pelo teorema de Pitágoras.
Exercício 2. Use o resultado do exercício anterior e novamente o teorema de Pitágoras para determinar o comprimento do vetor $\vec{r}$ na Figura 3. Calcule o valor deste comprimento quando $x=4$ cm, $y=3$ cm e $z=5$ cm.
Exercício 3. Mostre que o comprimento do vetor $\vec{r}$ calculado no exercício anterior também pode ser obtido pela expressão $d(A,B)$ com o ponto $A$ sendo a origem $\mathcal{O}$ e o ponto $B$ sendo o ponto $m$ (veja a Figura 3).
2.3. Vetor posição
Um vetor com a origem fixa na origem de um sistema de coordenadas e com a ponta na posição de um objeto (em movimento ou não) é denominado de vetor posição. Como exemplo, veja o vetor \(\vec{r}\) na
Figura 1. Essencialmente, estamos usando vetores para representar posições. Em princípio não precisamos usar um vetor para localizar um ponto no espaço. No entanto, a noção de velocidade requer a presença de um vetor posição, como veremos adiante. Quando
há movimento, é importante especificar também a direção e o sentido deste movimento. Em outras palavras, precisamos saber para onde estamos indo, literalmente. Como veremos, vetores constituem uma linguagem matemática extremamente concisa, elegante
e prática para descrevermos posições, velocidades, acelerações e outras quantidades físicas, como forças, que necessitam de direção e sentido, além de intensidade, para serem especificadas completamente.
Vejamos então algumas propriedades importantes sobre vetores. Primeiro, vetores podem ser multiplicados por números, mantendo a direção e alterando o comprimento. O sentido será invertido somente se esse número for negativo. Segundo, vetores podem ser
somados (ou subtraídos) de acordo com a regra simples: a soma é nula se os vetores formarem um polígono fechado, com a ponta de um vetor no "pé'' do outro, como ilustrado na Figura 2 onde $\vec{A}+\vec{B}+\vec{C}=0$. Note que estamos assumindo que vetores
possam ser transportados (como flechas) sem que haja mudanças no comprimento, direção e sentido. Quando multiplicamos objetos por números e realizamos somas desses mesmos objetos, obtendo objetos do mesmo tipo, estamos realizando combinações lineares.
Por exemplo, na Figura 2 podemos formar a combinação linear $\vec{C}=-\vec{A}-\vec{B}$, entre outras possíveis.
Outra característica de um vetor, muito importante para a Física, é o seu comportamento em relação a rotações em torno de um eixo fixo e à inversões espaciais. Quando um vetor é rodado em torno de um eixo fixo, o comprimento do vetor não é alterado. Inversão espacial significa inverter o sentido, mantendo a direção e o comprimento inalterados ("virar ao avesso''). Um candidato a vetor (que tem comprimento, direção e sentido) que permanece invariante a uma inversão espacial é denominado de pseudo-vetor.
A descrição de vetores num sistema de coordenadas é muito frutífera. Vamos denotar por $\hat{r}$ (observe a notação) um vetor de comprimento unitário, o qual chamaremos de versor. O versor sempre indica a direção e o sentido de um determinado vetor. Sendo $r$ o comprimento do vetor $\vec{r}$, então $\vec{r}=r\hat{r}$, sempre. A Figura 1 exibe três versores, $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$: um versor para cada uma das três direções independentes. Observe na Figura 1 que podemos formar, naturalmente, a combinação linear $\vec{\rho} = x\hat{\imath} + y\hat{\jmath}$, bem como $\vec{r}= \vec{\rho} + z\hat{k}$. Portanto,
\begin{equation} \vec{r}=x\hat{\imath} + y\hat{\jmath} + z\hat{k}=(x,y,z), \quad r^{2}=x^{2}+y^{2}+z^{2},\end{equation}onde a notação $\vec{r}=(x,y,z)$ é conveniente (a ordem não pode ser alterada). As projeções $(x,y,z)$ são as coordenadas do vetor posição $r$ no sistema de coordenadas $\mathcal{O}$. Por exemplo, quando escritos nesta notação conveniente, a combinação linear entre os vetores $\vec{A}=(x_{a},y_{a},z_{a})$ e $\vec{B}=(x_{b},y_{b},z_{b})$ será
\begin{equation} \alpha\vec{A}+\vec{B}=(\alpha x_{a},\alpha y_{a},\alpha z_{a})+(x_{b},y_{b},z_{b})= (\alpha x_{a}+x_{b},\alpha y_{a}+y_{b},\alpha z_{a}+z_{b}). \end{equation}Vale observar que dado três vetores, não necessariamente num mesmo plano, pode ser que nenhuma combinação linear entre eles seja possível. Neste caso, estes vetores são denominados de linearmente independentes. Os três versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, mostrados na Figura 1, são linearmente independentes.
|

|
|---|---|
| Figura 1.
|
Figura 2.
|
Exercício 1. Desenhe os vetores posição $\vec{R}_{1}=(1,2,0)$ e $\vec{R}_{2}=(1,1,0)$ em um mesmo sistema cartesiano de coordenadas (ortonormal). Determine as coordenadas da soma $\vec{R}_{1}+\vec{R}_{2}$ e da diferença $\vec{R}_{1}-\vec{R}_{2}$ e represente-os no mesmo sistema de coordenadas anterior. Use o teorema de Pitágoras para determinar o comprimento de cada vetor.
Exercício 2. Primeiro note que as componentes dos versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ mostrados na Figura 1 são $\hat{\imath}=(1,0,0)$, $\hat{\jmath}=(0,1,0)$ e $\hat{k}=(0,0,1)$.
Agora tente escrever, por exemplo, $\hat{k}=\alpha\hat{\imath}+\beta\hat{\jmath}$. Sabendo que a igualdade entre vetores somente é possível se houver uma igualdade entre suas componentes em cada direção, mostre que a combinação linear $\hat{k}=\alpha\hat{\imath}+\beta\hat{\jmath}$
resulta em três equações lineares. Mostre que duas destas equações lineares envolvem os escalares $\alpha$ e $\beta$, cuja soluções são $\alpha=0$ e $\beta=0$. Verifique que a terceira equação é inconsistente ($0=1$). Isto mostra que os versores $\hat{\imath}$,
$\hat{\jmath}$ e $\hat{k}$ são linearmente independentes, isto é, não admitem uma combinação linear entre eles.
2.4. Produto escalar
Há outras operações binárias que podemos realizar com vetores, além da combinação linear? É possível inventar uma operação entre dois vetores que nos dê informações sobre seus comprimentos e o ângulo entre eles? Sim, é possível e muito útil. Vejamos.
Podemos construir uma operação binária envolvendo dois vetores cujo resultado é um número real. Esta operação binária entre os vetores \(\vec{A}\) e $\vec{B}$, denotada por $\vec{A}\cdot\vec{B}\in \mathbb{R}$, será denominada de produto escalar.
O produto escalar é definido requerendo que ele satisfaça as propriedades seguintes.
- Simetria: $\displaystyle \vec{A}\cdot\vec{B} = \vec{B}\cdot\vec{A}\in \mathbb{R}$.
- Linearidade:$\displaystyle \vec{C}\cdot(\alpha\vec{A}+\beta\vec{B})= \alpha\,\vec{C}\cdot\vec{A} + \beta\,\vec{C}\cdot\vec{B},\; \alpha,\beta\in \mathbb{R}$.
- Positivo definido: $\displaystyle \vec{A}\cdot\vec{A}=0\iff\vec{A}=\vec{0},\; \vec{A}\cdot\vec{A}>0\iff\vec{A}\ne\vec{0}$.
- Mensurabilidade: $\displaystyle A\equiv||\vec{A}||\equiv\sqrt{\vec{A}\cdot\vec{A}}$.
A propriedade 1 expressa que o produto escalar é uma operação binária simétrica (ou comutativa). A propriedade 2 significa que o produto escalar é linear, pois obedece a propriedade distributiva. Note que os números $\alpha$ e $\beta$ podem ser retirados
livremente de dentro do produto escalar. A propriedade 3 garante que o produto escalar seja bem comportado (não-degenerado), pois evita que o produto escalar de um vetor com ele mesmo seja nulo sem que o vetor seja nulo. A propriedade 4 garante que
o comprimento, também conhecido por módulo ou norma, seja calculado pelo produto escalar. Note que a propriedade 3 está em sintonia com a definição
de comprimento como uma quantidade real positiva ou nula. Comprimento nulo quando, e somente quando, o vetor for nulo. O produto escalar é um instrumento (analítico) de medida do comprimento de um vetor.
Uma questão importante é: como realizar esta operação binária, denominada de produto escalar, em termos de coordenadas? ou seja, como tornar o produto escalar operacional? Graças à propriedade distributiva 2, basta conhecermos todos os produtos escalares possíveis entres os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, colocados ao longo dos três eixos independentes do espaço euclidiano (veja a Figura 1). Desta forma, teremos, em princípio, nove produtos escalares a serem determinados, pois cada vetor pode ser escrito como uma combinação linear dos versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ do sistema de coordenadas escolhido. No entanto, a propriedade de simetria, reduz para seis o número de produtos escalares que devemos conhecer. Uma forma eficiente de guardarmos estes produtos escalares é utilizando um arranjo matricial, isto é, uma matriz $3\times 3$,
\begin{equation} \label{eq:metrica} g\equiv (g_{ij})\equiv \begin{pmatrix} \hat{\imath}\cdot\hat{\imath} & \hat{\imath}\cdot\hat{\jmath} & \hat{\imath}\cdot\hat{k} \\ \hat{\jmath}\cdot\hat{\imath} & \hat{\jmath}\cdot\hat{\jmath} & \hat{\jmath}\cdot\hat{k} \\ \hat{k}\cdot\hat{\imath} & \hat{k}\cdot\hat{\jmath} & \hat{k}\cdot\hat{k} \end{pmatrix}. \end{equation}Esta matriz é denominada de métrica (por razões óbvias). É sempre bom procurarmos por expressões matemáticas mais sintéticas. Simplesmente rebatizando os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ para
\begin{equation} \label{eq:ijke} \hat{e}_{1}\equiv\hat{\imath},\; \hat{e}_{2}\equiv\hat{\jmath},\; \hat{e}_{3}\equiv\hat{k}, \end{equation}podemos reescrever os elementos de matriz da métrica como (verifique)
\begin{equation} \label{eq:gij} g_{ij}=\hat{e}_{i}\cdot\hat{e}_{j}=g_{ji},\; i,j\in\{1,2,3\}. \end{equation}Além de mais simples é também muito elegante. Note que a simetria da métrica é uma consequência direta da simetria do produto escalar.
Considere agora dois vetores escritos num mesmo referencial, como aquele mostrado na Figura 1, com os versores escritos como acima, em termos de $\hat{e}_{i}$. Seja então
\begin{equation} \label{eq:vecAc} \vec{A}=\sum\limits_{i=1}^{3}A_{i}\hat{e}_{i}= A_{1}\hat{e}_{1}+A_{2}\hat{e}_{2}+A_{3}\hat{e}_{3}= (A_{1},A_{2},A_{3}) \end{equation} e \begin{equation} \label{eq:vecBc} \vec{B}=\sum\limits_{i=1}^{3}B_{i}\hat{e}_{i}= B_{1}\hat{e}_{1}+B_{2}\hat{e}_{2}+B_{3}\hat{e}_{3}= (B_{1},B_{2},B_{3}). \end{equation}Agora use todas as propriedades do produto escalar para calcular explicitamente, de preferência usando os somatórios,
\begin{equation} \label{eq:ABg} \vec{A}\cdot\vec{B}= \left(\sum\limits_{i=1}^{3}A_{i}\hat{e}_{i}\right)\cdot \left(\sum\limits_{j=1}^{3}B_{j}\hat{e}_{j}\right)= \sum\limits_{i,j=1}^{3}A_{i}B_{j}\,\hat{e}_{i}\cdot\hat{e}_{j}= \sum\limits_{i,j=1}^{3}A_{i}B_{j}\,g_{ij}. \end{equation}
Note o uso de índices distintos ($i$ e $j$) no momento de escrever cada um dos vetores em coordenadas. Cada soma requer um índice distinto. Não economize nos índices. Este mesmo resultado pode ser reobtido usando produtos matriciais (linhas por colunas).
Basta usar o vetor $\vec{A}=(A_{i})=(A_{1},A_{2},A_{3})$ como uma matriz linha $(A_{j})$ e o vetor $\vec{B}$ como uma matriz coluna (a transposta), $(B_{j})^{\textrm{T}}$.
- Teorema 1
- Sejam $\vec{A}$ e $\vec{B}$ dois vetores descritos numa base qualquer dada pela métrica $g$. Então, o produto escalar entre eles é \begin{equation} \vec{A}\cdot\vec{B} = (A_{i})\, g\, (B_{j})^{\textrm{T}}. \end{equation}
Afinal de contas, como poderemos calcular os produtos escalares que aparecem na métrica? Não podemos! Estes produtos escalares devem ser fornecidos no momento em que compramos o referencial. Para entendermos melhor esta situação, devemos nos perguntar: qual é o significado geométrico do produto escalar?
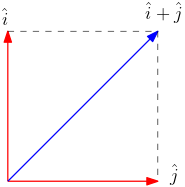
Para entendermos melhor o significado geométrico do produto escalar, devemos calcular primeiro o produto escalar entre dois vetores perpendiculares (ortogonais). Vamos usar os versores $\hat{\imath}$ e $\hat{\jmath}$ como dois representantes típicos de vetores ortogonais. Como indicado na Figura 2, o comprimento da soma vetorial $\hat{\imath} + \hat{\jmath}$ é a hipotenusa do triângulo retângulo formado pelos versores $\hat{\imath}$ e $\hat{\jmath}$. Como os versores possuem comprimentos unitários, por definição, então a hipotenusa pode ser calculada usando o teorema de Pitágoras,
\begin{equation} \label{eq:peij1} ||\hat{\imath} + \hat{\jmath}||^{2} = ||\hat{\imath}||^{2} + ||\hat{\jmath}||^{2}=2. \end{equation}Sim, você tem razão. Naturalmente, o valor da hipotenusa também pode ser calculado usando o produto escalar para calcular o comprimento de um vetor,
\begin{equation} \label{eq:peij2} ||\hat{\imath} + \hat{\jmath}||^{2} = (\hat{\imath} + \hat{\jmath})\cdot (\hat{\imath} + \hat{\jmath}) = ||\hat{\imath}||^{2} + ||\hat{\jmath}||^{2} + 2\hat{\imath}\cdot\hat{\jmath}=2+2\hat{\imath}\cdot\hat{\jmath}, \end{equation}onde usamos também a propriedade distributiva do produto escalar. Comparando estes dois resultados, concluímos que $\hat{\imath}\cdot\hat{\jmath}=0$. Isto significa que o produto escalar entre dois vetores ortogonais é nulo. Este resultado continua valendo mesmo para vetores não-unitários, seguindo o mesmo raciocínio anterior. Portanto ele é um teorema:
- Teorema 2
- Sejam $\vec{A}$ e $\vec{B}$ dois vetores perpendiculares. Então, $\displaystyle\vec{A}\cdot\vec{B}=0\quad\iff \quad \vec{A}\perp\vec{B}$.
Portanto, sabemos o significado de cada elemento na diagonal da métrica: são os comprimentos (ao quadrado) dos versores. Para o sistema de coordenadas cartesiano da Figura 1, os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ são unitários (possuem comprimentos iguais a um).
E quando os vetores não são perpendiculares? qual é o significado do produto escalar? Considere dois vetores arbitrários $\vec{A}$ e $\vec{B}$, formando um ângulo $\theta$ entre eles. Dois vetores sempre estão em um plano, como mostrado na Figura 3. Escolha neste plano um vetor $\vec{C}$ perpendicular a $\vec{B}$. Naturalmente, os versores $\hat{B}$ e $\hat{C}$ formam uma base ortonormal para o vetor $\vec{A}$, isto é, podemos escrever $\vec{A} = A\cos\theta\,\hat{B} + A\sin\theta\,\hat{C}$. Efetue agora o produto escalar $\vec{A}\cdot\hat{B}$ e use o Teorema 1. Resulta (verifique) que $A\cos\theta= \vec{A}\cdot\hat{B}$. O produto escalar $\vec{A}\cdot\hat{B}$ é exatamente a projeção do vetor $\vec{A}$ sobre o versor $\hat{B}$ (ou na direção do vetor $\vec{B}$). Note na Figura 1 que $\vec{r}\cdot\hat{\imath}=x$, $\vec{r}\cdot\hat{\jmath}=y$ e $\vec{r}\cdot\hat{k}=z$, ou seja, as coordenadas são as projeções do vetor sobre os versores da base. Naturalmente, os papeis de $\vec{A}$ e $\vec{B}$ podem ser perfeitamente invertidos. Assim, temos um segundo teorema.
- Teorema 3
- Sejam $\vec{A}$ e $\vec{B}$ dois vetores formando um ângulo $\theta$ entre eles. Então, $\displaystyle \vec{A}\cdot\vec{B}=AB\cos\theta$.
Note que este teorema nos permite calcular o produto escalar entre dois vetores sem a necessidade de escrevê-los em um determinado sistema de coordenadas, basta conhecermos seus comprimentos e o ângulo entre eles. Vetores são flechas e existem independentemente de um referencial (sistema de coordenadas).
Resumindo: além do comprimento, o produto escalar nos dá também uma informação sobre a orientação relativa entre vetores. Também é importante notar que o Teorema 2 nos fornece uma forma operacional para calcularmos o produto escalar entre vetores quando seus comprimentos e o ângulo entre eles são conhecidos previamente.
Voltemos ao nosso problema original: o sistema cartesiano da Figura 1. Nele, escolhemos os três versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ mutuamente ortogonais (perpendiculares), isto é, os ângulos entre estes versores é de 90 graus. Portanto, usando o Teorema 1, a métrica desse sistema de coordenadas é
\begin{equation} \label{eq:identidade} g = \begin{pmatrix} \hat{\imath}\cdot\hat{\imath} & \hat{\imath}\cdot\hat{\jmath} & \hat{\imath}\cdot\hat{k} \\ \hat{\jmath}\cdot\hat{\imath} & \hat{\jmath}\cdot\hat{\jmath} & \hat{\jmath}\cdot\hat{k} \\ \hat{k}\cdot\hat{\imath} & \hat{k}\cdot\hat{\jmath} & \hat{k}\cdot\hat{k} \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}, \end{equation}ou seja, ela é a matriz identidade para um sistema de coordenadas ortonormal. Isto simplifica muito nossa vida e explica a importância prática de usarmos sistemas ortonormais (versores ortogonais e unitários) de coordenadas. Assim, podemos escrever o produto escalar entre dois vetores arbitrários $\vec{A}=(A_{x},A_{y},A_{z})$ e $\vec{B}=(B_{x},B_{y},B_{z})$, em um sistema de coordenadas ortonormal cartesiano simplesmente multiplicando componentes na mesma direção e somando (verifique)
\begin{equation} \label{eq:pescalar7} \vec{A}\cdot\vec{B}= A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}\quad (\ast). \end{equation}Como mais um teste de consistência, use $(\ast)$ para calcular o comprimento do vetor posição $\vec{r}$ da Figura 1 e veja que é o mesmo valor obtido diretamente das projeções indicadas na mesma figura.
Também é importante ter em mente que a expressão $(\ast)$ é válida somente em um sistema ortonormal de coordenadas. Caso a base não seja ortonormal, devemos usar a métrica apropriada em todas as operações envolvendo o produto escalar. Também devemos ter
em mente que a métrica vem junto com a base, ela é um conjunto de ``especificações técnicas'' sobre a base, uma espécie de ``manual de instruções''. Se alguém lhe vender uma base sem a métrica, entre em contato com o Procon mais próximo.
Uma vez que as coordenadas dos vetores $\vec{A}$ e $\vec{B}$ são conhecidas em um sistema ortonormal de coordenadas, então podemos usar $(\ast)$ para calcular (em termos das coordenadas) o valor do produto escalar que aparece no lado esquerdo do Teorema
2, bem como os módulos $A$ e $B$ que aparecem no lado direito. Assim, poderemos usar o Teorema 2 para calcular o ângulo entre dois vetores.
Exercício 1. Trabalhe detalhadamente todas as situações especificadas por "Verifique".
Exercício 2. Efetue o produto escalar entre os vetores posição $\vec{R}_{1}=(1,2,1)$ e $\vec{R}_{2}=(1,1,2)$. Calcule também o comprimento de cada um deles bem como o ângulo entre eles. Repita este procedimento para os vetores resultantes da soma e da diferença entre $\vec{R}_{1}$ e $\vec{R}_{2}$. Considere um sistema ortonormal de coordenadas.
Exercício 3. Suponha que uma determinada base tenha a seguinte métrica:
\begin{equation} \label{eq:gqq} g = \begin{pmatrix} 1 & 0.5 & 0\\ 0.5 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}. \end{equation}Determine os ângulos entre os versores desta base e desenhe-a. Suponha que $\vec{R}_{1}=(1,2,1)$ e $\vec{R}_{2}=(1,1,2)$ sejam dois vetores escritos nesta base. Determine seus comprimentos e o produto escalar e o ângulo entre eles. Desenhe-os nesta base.
| Figura 1. Referencial ortonormal.
|
Figura 2. Teorema 1.
|
Figura 2. Teorema 2.
|
|---|---|---|

|
|

|
2.5. Produto vetorial
Definição. Há somente mais uma operação binária com vetores que nos interessa (e muito). Desta vez, esta operação binária produzirá um novo vetor. Seja \(\mathbb{V}\) o conjunto de todos os
vetores. Esta nova operação binária entre os vetores $\vec{A}$ e $\vec{B}$, denotada por $\vec{A}\times\vec{B}\in \mathbb{V}$, será denominada de produto vetorial. Lembre-se que o produto
escalar produz um número real (escalar) e o produto vetorial produz um vetor (flecha). O produto vetorial é definido requerendo que ele satisfaça as propriedades seguintes.
- Anti-simetria: $\displaystyle \vec{A}\times\vec{B}=-\vec{B}\times\vec{A}$.
- Linearidade: $\displaystyle\vec{C}\times(\alpha\vec{A}+\beta\vec{B})=\alpha(\vec{C}\times\vec{A})+\beta(\vec{C}\times\vec{B}),\; \alpha,\beta\in \mathbb{R}$.
- Perpendicularidade: $\displaystyle\vec{C}\equiv\vec{A}\times\vec{B}\implies\vec{C}\cdot\vec{A}=\vec{C}\cdot\vec{B}=0$
- Orientabilidade: $\displaystyle (\vec{A},\vec{B},\vec{C})\leftrightarrow (\hat{\imath},\hat{\jmath},\hat{k}),\; \vec{C}\equiv\vec{A}\times\vec{B}$.
A propriedade 1 afirma que o produto vetorial, ao contrário do produto escalar, é anti-simétrico (troca de sinal quando os vetores trocam de posições). A propriedade 2 significa que o produto vetorial, assim como o produto escalar, é linear. Note que os escalares $\alpha$ e $\beta$ no lado direito podem ser retirados de dentro do produto vetorial (como no caso do produto escalar). A propriedade 3 significa que o vetor resultante $\vec{A}\times\vec{B}$ é, simultaneamente, perpendicular aos vetores $\vec{A}$ e $\vec{B}$.
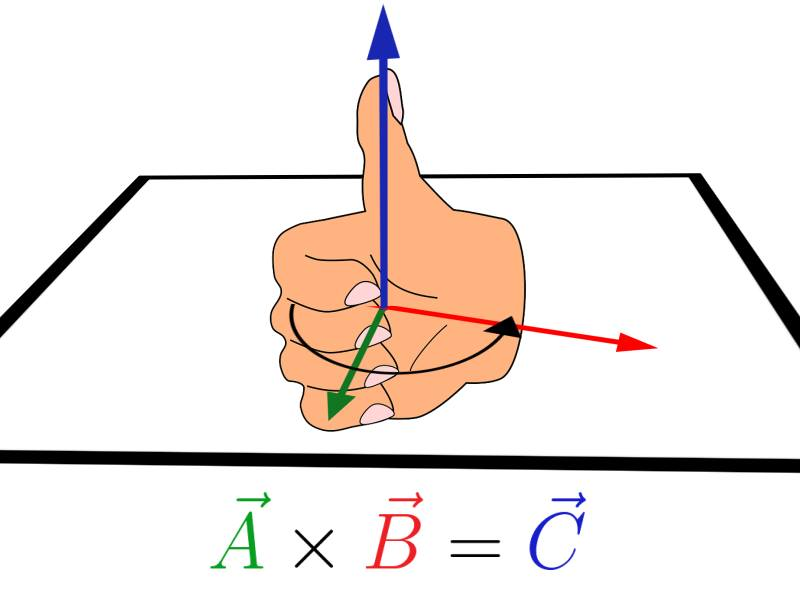
A propriedade 4 é uma novidade. O produto vetorial cria um vetor numa direção e que precisa de um sentido nesta direção. A propriedade 4 afirma que o sentido do vetor resultante $\vec{C}=\vec{A}\times\vec{B}$ na trinca $(\vec{A},\vec{B},\vec{A}\times\vec{B})$ é idêntico ao sentido do versor $\hat{k}$ na trinca de versores $(\hat{\imath},\hat{\jmath},\hat{k})$ de um referencial ortonormal. É equivalente à regra da mão direita indicada na Figura 1: o sentido do vetor resultante $\vec{C}=\vec{A}\times\vec{B}$ é indicado pelo nosso polegar direito quando movimentamos os demais dedos da mão direita no sentido de $\vec{A}$ para $\vec{B}$. Note que a propriedade 4 é uma escolha para a orientação do produto vetorial (estamos usando a regra da mão direita para estabelecer uma orientação espacial).
Teoremas. Como podemos calcular as componentes do vetor resultante $\vec{C}=\vec{A}\times\vec{B}$ a partir das componentes dos vetores $\vec{A}=(A_{x},A_{y},A_{z})$ e $\vec{B}=(B_{x},B_{y},B_{z})$? Isto pode ser feito em duas etapas. Primeiro observe que a propriedade 3 nos fornece as seguintes relações (verifique):
\begin{equation} C_{x}A_{x}+C_{y}A_{y}+C_{z}A_{z}=0,\; C_{x}B_{x}+C_{y}B_{y}+C_{z}B_{z}=0. \end{equation}Note que estamos pressupondo que estes vetores estejam decompostos numa base ortonormal. Caso a base não seja ortonormal, devemos efetuar os produtos escalares usando a métrica apropriada. Destas relações, podemos escrever, por exemplo, as componentes $C_{x}$ e $C_{y}$ em função de $C_{z}$ (verifique),
\begin{equation} C_{x}=\frac{A_{y}B_{z}-A_{z}B_{y}}{A_{x}B_{y}-A_{y}B_{x}}C_{z},\; C_{y}=\frac{A_{z}B_{x}-A_{x}B_{z}}{A_{x}B_{y}-A_{y}B_{x}}C_{z}. \end{equation}Naturalmente, podemos reescrevê-las na forma (verifique)
\begin{equation} \label{eq:pvC3} \frac{C_{x}}{A_{y}B_{z}-A_{z}B_{y}} = \frac{C_{y}}{A_{z}B_{x}-A_{x}B_{z}} =\frac{C_{z}}{A_{x}B_{y}-A_{y}B_{x}} = \beta,\end{equation}onde $\beta$ é um número real arbitrário e independente das coordenadas dos vetores $\vec{A}$ e $\vec{B}$. Estas razões devem ser válidas para quaisquer vetores $\vec{A}$ e $\vec{B}$. Desta forma, temos as componentes do vetor $\vec{C}$, resultante do produto vetorial $\vec{A}\times\vec{B}$, em termos das componentes dos vetores $\vec{A}$ e $\vec{B}$ e da constante arbitrária $\beta$. Mas como esta constante $\beta$ é arbitrária, então podemos escolher um valor para ela: $\beta=1$. Não se assuste, como veremos adiante, há várias razões práticas para tal escolha. Com $\beta=1$, temos mais um teorema.
- Teorema 4
- As componentes (base ortonormal) do produto vetorial $\vec{C}=\vec{A}\times\vec{B}$ são: \begin{equation} C_{x}=A_{y}B_{z}-A_{z}B_{y},\; C_{y}=A_{z}B_{x}-A_{x}B_{z},\; C_{z}=A_{x}B_{y}-A_{y}B_{x}. \end{equation}
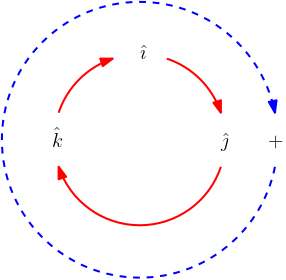
Como veremos através de vários exemplos, escolher $\beta$ como sendo um número positivo está condizente com a propriedade 4 (regra da mão direita) do produto vetorial. Caso tivéssemos escolhido um número negativo para $\beta$, teríamos que usar uma regra da mão esquerda. Note que a disposição dos índices $x$, $y$ e $z$ nas expressões dadas no Teorema 4 segue uma ordem cíclica, com valores positivos no sentido horário, $\{(x,y,z),(z,x,y),(y,z,x)\}$, e com valores negativos no sentido anti-horário, $\{(x,z,y),(y,x,z),(z,y,x)\}$. Veja a Figura 2, com $(\hat{\imath},\hat{\jmath},\hat{k})$ trocados por $(x,y,z)$, para uma ilustração de mais uma regra mnemônica.
Tendo as componentes do vetor $\vec{C}$, oriundo do produto vetorial $\vec{A}\times\vec{B}$, podemos calcular seu módulo usando o produto escalar. Após um pouco de paciência, encontraremos (verifique)
\begin{equation} C^{2}=||\vec{C}||^{2}=\vec{C}\cdot\vec{C}=A^{2}B^{2}-(\vec{A}\cdot\vec{B})^{2}, \end{equation}a qual pode ser perfeitamente reescrita, usando o Teorema 2, em termos do ângulo $\theta$ entre $\vec{A}$ e $\vec{B}$,
\begin{equation} C^{2}=A^{2}B^{2}-A^{2}B^{2}\cos^{2}\theta=(AB)^{2}\sin^{2}\theta. \end{equation}Portanto, temos outro teorema.
- Teorema 5
- O módulo do vetor $\vec{C}= \vec{A}\times\vec{B}$ pode ser convenientemente calculado por $\displaystyle C=AB\,|\!\sin\theta|$.
Este teorema nos permite calcular o comprimento do vetor resultante de um produto vetorial a partir dos comprimentos dos vetores iniciais e do ângulo entre eles, sem a necessidade de escrevê-los em um sistema de coordenadas. Esta situação é análoga àquela relacionada com o Teorema 2.
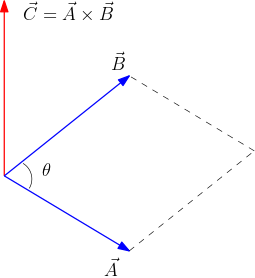
Significado geométrico. Vimos anteriormente que um produto escalar está associado com a projeção de um vetor sobre o outro. E o produto vetorial? ele tem alguma interpretação geométrica? Sim, ele tem e é muito relevante. Note que a expressão $AB\,|\!\sin\theta|$ é numericamente igual à área do paralelogramo de lados $A=||\vec{A}||$ e $B=||\vec{B}||$, formado pelos vetores $\vec{A}$ e $\vec{B}$ (veja a Figura 3 para se convencer disto). Note que a escolha $\beta=1$ permite esta interpretação. Caso contrário ($\beta\neq 1$), teríamos a área do paralelogramo multiplicada pelo valor de $\beta$. Desta forma, podemos adotar esta interpretação geométrica como mais uma propriedade na definição do produto vetorial (para fixar o valor $\beta=1$). Esta propriedade geométrica será usada para derivarmos uma das leis de Kepler para o movimento planetário.
Vejamos outras consequências do Teorema 4. A propriedade 5 significa que o produto vetorial entre dois vetores paralelos (ou anti-paralelos) resulta em um vetor nulo, pois neste caso o ângulo entre eles é 0 graus (ou 180 graus). Esta propriedade, juntamente com a regra da mão direita nos permite calcular todos os produtos vetoriais entre os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ de uma base ortonormal:
\begin{equation} \label{eq:ijk} \hat{\imath} = \hat{\jmath}\times\hat{k},\quad \hat{\jmath} = \hat{k}\times\hat{\imath}, \quad \hat{k} = \hat{\imath}\times\hat{\jmath}. \end{equation}Notas.
- Observando os produtos vetoriais entre os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, percebemos que a regra da mão direita é equivalente a efetuarmos permutações circulares nos versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, tomando o sentido horário como positivo, como indicado na Figura 2.
- A escolha $\beta=1$ no cálculo das componentes do produto vetorial garante que o versor resultante $\hat{\imath} = \hat{\jmath}\times\hat{k}$ seja unitário.
- Usando os produtos vetoriais entre os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ e a propriedade de linearidade, podemos calcular o produto vetorial entre dois vetores arbitrários escritos explicitamente em termos de uma base ortonormal.
- Mencionamos anteriormente que um pseudo-vetor não inverte o seu sentido perante uma inversão espacial. Sendo assim, um produto vetorial é um pseudo-vetor, pois invertendo os sentidos de $\vec{A}$ e $\vec{B}$, simultaneamente, em $\vec{A}\times\vec{B}$
nada de novo acontece. Em Física, temos vários pseudo-vetores importantes. Iremos trabalhar com dois deles em Mecânica: momentum angular $\vec{L}=\vec{r}\times\vec{p}$ e torque $\vec{\tau}=\vec{r}\times\vec{F}$, onde $\vec{r}$ é o vetor posição, $\vec{p}$
é o momentum linear ($\vec{p}=m\vec{v}$) e $\vec{F}$ é a força resultante atuando no centro de massa de um objeto de massa $m$. Nas nossas aplicações iremos usar também a força de Lorentz, outro pseudo-vetor importante, $\vec{F}_{L}=q\,\vec{v}\times\vec{B}$,
produzida por um campo magnético $\vec{B}$ sobre uma carga $q$ em movimento com uma velocidade $\vec{v}$.
Exercício 1. Trabalhe detalhadamente todas as situações especificadas por "Verifique".
Exercício 2. Efetue o produto vetorial $\vec{R}_{3}=\vec{R}_{1}\times\vec{R}_{2}$ entre os vetores posição $\vec{R}_{1}=(1,2,1)$ e $\vec{R}_{2}=(1,1,2)$. Calcule os comprimentos de cada vetor,
bem como os ângulos entre eles. Faça uma representação gráfica destes vetores. Calcule também a área de cada paralelogramo formado por cada par de vetores. Considere um sistema ortonormal de coordenadas.
Exercício 3. Verifique que as componentes do vetor resultante de um produto vetorial também podem ser calculadas através do determinante
\begin{equation} \label{eq:pvdet} \vec{A}\times\vec{B} = \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ A_{x} & A_{y} & A_{z} \\ B_{x} & B_{y} & B_{z} \end{vmatrix}. \end{equation}Exercício 4. Usando coordendas, verifique a identidade (muito útil) $\vec{A}\times(\vec{B}\times\vec{C})= \alpha\vec{B}-\beta\vec{C}$, onde $\alpha=\vec{A}\cdot\vec{C}$ e $\beta=\vec{A}\cdot\vec{B}$. Note que não uma componente na direção do vetor $\vec{B}$.
| Figura 1. Regra da mão direita.
|
Figura 2. Regra cíclica.
|
Figura 3. Paralelogramo.
|
|---|---|---|
|
|
|
2.6. Produto misto
O produto misto envolve um produto vetorial seguido de um produto escalar, nessa ordem. A sua definição é: dado três vetores \(\vec{A}\), $\vec{B}$ e $\vec{C}$ quaisquer, o produto misto é um número definido por $\vec{C}\cdot(\vec{A}\times\vec{B})$ (veja a Figura 1). Note que temos de executar primeiro o produto vetorial $\vec{A}\times\vec{B}$, o qual resultará em um vetor, para depois calcularmos o produto escalar com $\vec{C}$, resultando em um número. Que acontece se as posições dos três vetores no produto misto $\vec{C}\cdot(\vec{A}\times\vec{B})$ forem modificadas simultaneamente, por exemplo para $\vec{B}\cdot(\vec{C}\times\vec{A})$? Nada! O produto misto é invariante por permutações circulares (cíclicas) das letras $A$, $B$ e $C$,
- Teorema 6
- O produto misto é invariante por permutações circulares (cíclicas), \begin{equation} \vec{A}\cdot(\vec{B}\times\vec{C}) = \vec{C}\cdot(\vec{A}\times\vec{B}) = \vec{B}\cdot(\vec{C}\times\vec{A}). \end{equation}
Uma forma de provar esta propriedade é fazendo uso do determinante para calcular o produto vetorial (verifique):
\begin{equation} \label{eq:prodmistodet} \vec{A}\cdot(\vec{B}\times\vec{C}) = \vec{A}\cdot \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ B_{x} & B_{y} & B_{z}\\ C_{x} & C_{y} & C_{z} \end{vmatrix} = \begin{vmatrix} A_{x} & A_{y} & A_{z}\\ B_{x} & B_{y} & B_{z}\\ C_{x} & C_{y} & C_{z} \end{vmatrix}. \end{equation}
Note que as permutações cíclicas efetuadas no produto misto correspondem a quatro trocas de linhas no último determinante, deixando-o inalterado. Portanto, do ponto de vista operacional, o produto misto está muito bem compreendido.
E o significado geométrico do produto misto? Muito bem, você está aprendendo rápido as regras do nosso jogo. O produto misto é numericamente igual ao volume do paralelepípedo formado pelos três vetores $\vec{A}$, $\vec{B}$ e $\vec{C}$ conforme ilustrado
pela Figura 1. Acompanhe a demonstração trabalhando o Exercício 2.
Exercício 1. Trabalhe detalhadamente todas as situações especificadas por "Verifique".
Exercício 2. Calcule o produto misto entre os vetores posição $\vec{A}=(1,2,1)$, $\vec{B}=(1,1,2)$ e $\vec{C}=(1,1,-1)$ mostrados na Figura 1. Calcule também os ângulos entre esses vetores
e seus comprimentos.
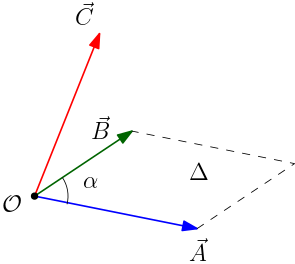
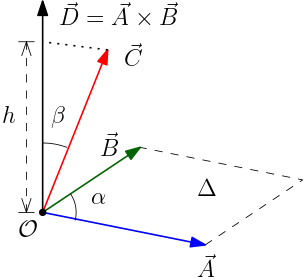
Exercício 3. Prove a propriedade geométrica do produto misto. Resolução. O volume de uma paralelepípedo é igual ao produto da área de uma de suas faces pela altura (perpendicular à face escolhida). Implemente esta estratégia com os passos seguintes.
- Calcule a área $\Delta$ da face formada pelos vetores $\vec{A}$ e $\vec{B}$: $\Delta=||\vec{A}\times\vec{B}||=AB\,\mathrm{sen}\,\alpha$, onde $A=||\vec{A}||$ e $B=||\vec{B}||$ (veja a Figura 2).
- Calcule a altura $h$ projetando o vetor $\vec{C}$ na direção perpendicular a plano dos vetores $A$ e $B$: $h=\vec{C}\cdot\hat{D}=C\,\mathrm{cos}\,\beta$ com $\hat{D}=\vec{A}\times\vec{B}/||\vec{A}\times\vec{B}||$ e $C=||\vec{C}||$ (veja a Figura 3).
- Portanto, o volume $v$ do paralelepípedo é $v=ABC\,\mathrm{sen}\,\alpha\,\mathrm{cos}\,\beta= \vec{C}\cdot(\vec{A}\times\vec{B})$. Verifique numericamente esta primeira igualdade usando os dados do Exercício 2.
| Figura 1.
|
Figura 2.
|
Figura 3.
|
|---|---|---|
 |
 |
 |
2.7. Curvas espaciais
Curvas espaciais
Tendo estabelecido propriedades importantes sobre o espaço euclidiano, temos que precisar a noção de trajetória de um objeto em movimento neste espaço. Qual é a noção cotidiana de trajetória que temos? Eu a vejo como um sequência de fotografias de um
objeto em movimento, tiradas em intervalos de tempo muito pequenos, com as posições do objeto ligadas por retas. Se os intervalos de tempo são muito pequenos, a trajetória terá a aparência de uma curva espacial, um curva suave em três dimensões. Isto
é tudo que precisamos para estabelecer uma estrutura matemática geral para qualquer trajetória. Portanto, nosso problema agora é como representar uma curva no espaço Euclidiano de forma eficiente, i.e., tendo um sistema de coordenadas Cartesiano
(de preferência ortonormal), temos de encontrar uma forma adequada (para a Mecânica) para representarmos analiticamente uma curva em termos de coordenadas. É o programa cartesiano: transformar objetos geométricos em números.
Definição.
Definição. Uma curva espacial \(\gamma\) é definida como o lugar geométrico dos pontos
\begin{equation} \label{eq:curva3d} \gamma: \vec{r}(t)=(x(t),y(t),z(t)),\; t\in\mathbb{R}. \end{equation}Note que estamos usando as coordenadas de um vetor posição $\vec{r}$, descrito em algum referencial ortonormal, para descrever as coordendas de um ponto na curva $\gamma$. Naturalmente, esse vetor posição identifica a posição de um objeto na sua trajetória, descrita pela curva espacial $\gamma$. Muito conveniente, não acha? Ainda mais conveniente é adiantar que a segunda lei de Newton nos obriga a interpretar o parâmetro $t$ na definição como sendo o tempo, medido por nossos relógios. Para o geômetra, esse parâmetro $t$ não precisa de um significado específico. Eles preferem o próprio comprimento da trajetória! Uma curva descrita como na definição está na sua forma paramétrica, onde $t$ é o parâmetro, o qual pertence a algum intervalo da reta real. Denominaremos as coordenadas $x(t)$, $y(t)$ e $z(t)$, ou simplesmente $x_{i}(t)$, de equações horárias (por razões óbvias, pois $t$ será o tempo). Vale mencionar que a forma paramétrica é também a forma mais eficiente computacionalmente em duas dimensões e única em três ou mais dimensões.
Exemplos.
Reta. A forma paramétrica de uma reta exige que as sua equações horárias sejam polinômios de segundo grau no parâmetro escolhido,
\begin{equation} \label{eq:reta} x_{i}(t)=a_{i}+b_{i}\, t,\; i\in\{1,2,3\}. \end{equation}Parábola. A forma paramétrica de uma parábola exige que as sua equações horárias sejam polinômios de segundo grau no parâmetro escolhido,
\begin{equation} \label{eq:parabola} x_{i}(t)=a_{i}+b_{i}\, t+c_{i}\, t^{2},\; i\in\{1,2,3\}. \end{equation}Círculo. A forma paramétrica de uma círculo de raio $R$ é dada pelas equações horárias
\begin{equation} \label{eq:circulo} x_{i}(t)=c_{i}+a_{i}R\,\cos\theta(t)+b_{i}R\,\sin\theta(t),\; i\in\{1,2,3\}. \end{equation}Espiral. Por comodidade, uma espiral de base circular de raio $R$, centrada no eixo $Z$, tem a forma paramétrica dada pelas equações horárias
\begin{equation} \label{eq:espiral} x(t)=R\,\cos\theta(t),\; y(t)=R\,\sin\theta(t),\; z(t)=f(t), \end{equation}onde a fase $\theta(t)$ é arbitrária e $f(t)$ é uma função racional de
$t$.
Questões. Será possível criar ferramentas matemáticas para nos informar se uma dada curva descrita pela sua forma paramétrica é, na verdade, uma reta? ou quando ela é plana? Existe um algoritmo para colocarmos uma reta tangente num determinado ponto de uma curva espacial? Como podemos calcular algebricamente o comprimento de um determinado trecho de uma curva espacial? As respostas a esta questões estão nas próximas seções.
Exercício. Use o Geogebra para criar e visualizar pelo menos um caso de cada curva exemplificada aqui. Visite a Seção Computação.
3. Taxas (Derivadas)
Uma trajetória \(\gamma\) é representada por uma curva espacial na sua forma paramétrica, $\gamma(t): (x(t),y(t),z(t))$, com o tempo $t$ como parâmetro natural. Seja $\vec{r}(t)$ o vetor posição de um ponto nesta trajetória, correspondente a um valor
do parâmetro $t$, ou, equivalentemente, num dado instante de tempo $t$. Utilizando um sistema ortonormal de coordenadas, base ordenada $\{\hat{i},\hat{j},\hat{k}\}$, este vetor posição é descrito como
Observe que o vetor posição:
- é uma função (vetorial) do tempo (parâmetro) $t$;
- representa (localiza) um ponto na trajetória;
- representa, via suas coordenadas, a própria trajetória.
Como esse vetor posição varia ao longo da trajetória? É possível descrever a taxa de variação do vetor posição como uma função (vetorial) do tempo (parâmetro) $t$?
3.1. Velocidade
A taxa de variação do vetor posição é denominada de velocidade. A velocidade é um vetor e uma função do tempo \(t\). A construção desse vetor velocidade está ilustrada na Figura 1. Nesta figura, o
ponto na trajetória designado por $t$ está fixo, enquanto o ponto designado por $t+\Delta t$ está livre, com $\Delta t\geq 0$.

Seja $\Delta\vec{r}$ a diferença entre os vetores posição destes dois pontos,
Agora, num processo contínuo e suave, levemos o ponto designado por $t+\Delta t$ para as proximidades do ponto (fixo) designado por $t$. O parâmetro $t$ pode ser escolhido de tal forma que $\Delta t\to 0$ numa vizinhança muito pequena em torno do ponto
designado por $t$.
- Definição 1 (Velocidade)
- A taxa de variação do vetor posição, ou velocidade, é uma função vetorial definida pelo processo limite \begin{equation} \label{eq:vec-v} \vec{v}(t)=\lim\limits_{\Delta t\to 0} \frac{\Delta\vec{r}}{\Delta t}\equiv \frac{d\vec{r}}{dt}\equiv \dot{\vec{r}}, \quad (\ast)\end{equation} conhecido por derivada primeira.
Designaremos as coordenadas do vetor velocidade por $v_{i}(t)$ ou $\dot{x}_{i}(t)$, com $i\in\{x,y,z\}$ ou $i\in\{1,2,3\}$, dependendo da conveniência. Reservaremos o ponto (e somente o ponto) sobre o nome para representar a primeira derivada temporal
(e somente a derivada temporal, i.e., em relação ao tempo $t$, $dx/dt=\dot{x}$). Veja o Cap. 2 do Livro Apêndices para um guia sobre derivadas
para iniciantes.
Interpretação geométrica. A interpretação geométrica do vetor velocidade está na Figura 1. Antes do processo limite $\Delta t\to 0$, a direção do vetor diferença $\Delta\vec{r}$ é uma reta
secante, i.e., ela passa por dois pontos na trajetória. Após processo limite $\Delta t\to 0$, a direção do vetor velocidade é uma reta tangente, pois tem apenas um ponto de contato com a curva $\gamma$ que representa a trajetória. A direção tangente
definida por esse processo é única. A direção do vetor velocidade é tangente à trajetória. Assim, devemos sempre colocar o vetor velocidade iniciando na posição do objeto e na direção tangente à trajetória,
como mostrado na Figura 1. Bom lembrar que o vetor posição inicia sempre na origem do sistema de coordenadas (ponto $\mathcal{O}$).
Análise dimensional. Veja o Cap. 1 do Livro Apêndices para uma introdução à Análise
Dimensional. Uma análise dimensional do vetor velocidade mostra que suas dimensões são as mesmas de comprimento por tempo, $[\vec{v}]=[dx/dt]=\text{L}/\text{T}$. Note que estamos tratando as diferenciais $dx$ e $dt$ como quantidades (infinitesimalmente
pequenas) com as dimensões de comprimento e tempo, respectivamente. Lembre sempre que velocidade é um vetor, por definição, com dimensões de comprimento por tempo. Livre-se da concepção adquirida que velocidade é "espaço por tempo", a qual contém dois
erros graves: velocidade não é um escalar (espaço) e "espaço" é muito mais que o comprimento entre dois pontos num espaço. Usar "espaço percorrido por tempo gasto" não ajuda muito, mesmo se interpretar "espaço percorrido" como a distância percorrida
ou comprimento do trajeto. Velocidade é um vetor, por definição, e, como tal, deve ser grafado (com a flecha).
Rapidez. Denominaremos por rapidez o módulo do vetor velocidade,
Note que estamos usando a Propriedade 4 do produto escalar numa base ortonormal. Note também que a rapidez é um escalar, diferentemente da velocidade (um vetor). Veremos que a rapidez terá um papel importante no cômputo do comprimento de um trajeto.
Exemplo. Sim, um exemplo. Seja a trajetória circular no plano $z(t)=0$ dada pela forma paramétrica
sendo $\theta$ a fase dada por
onde $\omega$ é um parâmetro conhecido por frequência angular, $\varphi$ é a constante da fase e $R$ é o raio (igual ao comprimento do vetor posição). Então a Definição 1 nos permite calcular o vetor velocidade
Efetuando as derivadas temporais, teremos
Esse vetor velocidade tem algumas características interessantes. Ele é perpendicular ao vetor posição, $\vec{r}\cdot\vec{v}=0$, e seu módulo é constante, $v=\|\vec{v}\|=\omega R$. Resultado conhecido? Agora sabe de onde veio. Verifique. Sempre
que obtiver resultados algébricos, como esses, use análise dimensional para checar a consistência de seus resultados. Quais são as dimensões do parâmetro $\omega$? Como a fase (argumento de uma função trigonométrica) deve ser adimensional, então a dimensão
da frequência angular $\omega$ deve ser inverso de tempo, $[\omega]=1/\text{T}$. Desta forma, tanto a velocidade quanto a rapidez estão com as dimensões corretas, $[v]=[\omega R]=\text{L}/\text{T}$.
Exercício 1. Determine o vetor velocidade, e seu módulo, de um objeto na trajetória no plano $z=0$ dada pela curva (círculo) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\quad y(t)=R\sin(\omega t), \end{equation} onde $R$ é o raio. Mostre que o vetor velocidade é sempre perpendicular ao vetor posição.
Exercício 2. Determine o vetor velocidade, e seu módulo, de um objeto na trajetória no plano $z=0$ dada pela curva (parábola) na forma paramétrica \begin{equation} x(t)=2t,\; y(t)=3t-t^2,\;
0\leq t\leq 3/2. \end{equation} Observe o intervalo do parâmetro $t$ (tempo). Quais são o alcance e a altura máximas que esse objeto atinge? Em que respectivos tempos? Use o Sistema Internacional (SI) de unidades, onde comprimento está em metros (m)
e tempo em segundos (s).
Exercício 3. Determine o vetor velocidade, e seu módulo, de um objeto na trajetória dada pela curva (hélice) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\; y(t)=R\sin(\omega
t),\; z(t)=t/2. \end{equation} onde $\omega$ e o raio $R$ são parâmetros arbitrários.
3.2. Aceleração
A taxa de variação do vetor velocidade é denominada de aceleração. A aceleração é um vetor e uma função do tempo \(t\).
- Definição 2 (Aceleração)
- A taxa de variação do vetor velocidade, ou aceleração, é uma função vetorial definida pelo processo limite \begin{equation} \label{eq:vec-a} \vec{a}(t)=\lim\limits_{\Delta t\to 0} \frac{\Delta\vec{v}}{\Delta t}\equiv \frac{d\vec{v}}{dt}= \ddot{\vec{r}}. \quad (\ast\ast) \end{equation}
Importante notar que a aceleração é também a derivada segunda do vetor posição, $\vec{a}=\dot{\vec{v}}=\ddot{\vec{r}}$. Designaremos as coordenadas do vetor aceleração por $a_{i}(t)$, ou $\dot{v}_{i}(t)$, ou ainda $\ddot{x}_{i}(t)$, com $i\in\{x,y,z\}$
ou $i\in\{1,2,3\}$, dependendo da conveniência. Não teremos uma palavra especial para designar o módulo $a$ do vetor aceleração $\vec{a}$. As dimensões de aceleração são as mesmas de comprimento por tempo ao quadrado, $[\vec{a}]=[a]=\text{L}/\text{T}^{2}$.
Exemplo. Sim, um exemplo. Seja a trajetória circular no plano $z(t)=0$ dada pela forma paramétrica \begin{equation} x(t)=R\cos\theta(t),\; y(t)=R\sin\theta(t), \end{equation} sendo $\theta$
a fase dada por \begin{equation} \theta(t)=\omega t+\varphi, \end{equation} onde $\omega$ é um parâmetro conhecido por frequência angular, $\varphi$ é a constante da fase e $R$ é o raio (igual ao comprimento do vetor posição). Então a Definição 1 nos
permite calcular o vetor velocidade \begin{equation} \vec{v}=\dot{\vec{r}}=(\dot{x},\dot{y},\dot{z}). \end{equation} Efetuando as derivadas temporais, teremos \begin{equation} \begin{aligned} v_{x}&=\dot{x}=\dot{\theta}(-R\sin\theta)=-\omega R\sin\theta,\\
v_{y}&=\dot{y}=\dot{\theta}(+R\cos\theta)=+\omega R\cos\theta,\\ v_{z}&=\dot{z}=0. \end{aligned} \end{equation} Usando a Definição 2, o vetor aceleração é dado pelas derivadas temporais do vetor velocidade, \begin{equation} \vec{a}=\dot{\vec{v}}=(\dot{v}_{x},\dot{v}_{y},\dot{v}_{z}),
\end{equation} onde \begin{equation} \begin{aligned} a_{x}&=\dot{v}_{x}=-\omega^{2}R\cos\theta=-\omega^{2}x(t),\\ a_{y}&=\dot{v}_{y}=-\omega^{2}R\sin\theta=-\omega^{2}y(t),\\ a_{z}&=\dot{v}_{z}=0. \end{aligned} \end{equation} Esses vetores
posição, velocidade e aceleração têm algumas características interessantes. O vetor velocidade é perpendicular ao vetor posição, $\vec{r}\cdot\vec{v}=0$, e seu módulo é constante, $v=\|\vec{v}\|=\omega R$. O vetor aceleração está na mesma direção do
vetor posição, mas no sentido oposto (voltada para o centro, centrípeta), $\vec{a}=-\omega^{2}\vec{r}$, e seu módulo também é constante, $a=\|\vec{a}\|=\omega^{2}R=v^{2}/R$, onde a frequência angular $\omega$ foi eliminada em função da rapidez $v$.
Resultado conhecido? Agora sabe de onde veio. Verifique. Sempre que obtiver resultados algébricos, como esses, use análise dimensional para checar a consistência de seus resultados. Quais são as dimensões do parâmetro $\omega$? Como a fase (argumento
de uma função trigonométrica) deve ser adimensional, então a dimensão da frequência angular $\omega$ deve ser inverso de tempo, $[\omega]=1/\text{T}$. Desta forma, tanto a velocidade quanto a aceleração estão com as dimensões corretas, $[v]=[\omega
R]=\text{L}/\text{T}$ e $[a]=[\omega^{2} R]=\text{L}/\text{T}^{2}$, respectivamente.
Interpretação geométrica. Seja $v$ o módulo do vetor velocidade e $\hat{v}$ o seu versor, então, por definição $\vec{v}=v\hat{v}$. Note que o vetor $\vec{v}$ por ser a derivada do vetor posição, $\vec{v}=\dot{\vec{r}}$, é sempre tangente à trajetória (dada pela forma paramétrica representada por $\vec{r}$). Por isso, $\hat{v}$ também é conhecido por versor tangente. O vetor aceleração, a derivada do vetor velocidade, é \begin{equation} \label{eq:acelergeral} \vec{a} = \dot{\vec{v}} = \frac{d}{dt}(v\hat{v}) = \dot{v}\hat{v} + v\dot{\hat{v}}, \end{equation} onde usamos a regra da derivada de um produto de funções (do tempo), $\vec{v}=v\hat{v}$. Durante o movimento, a direção do vetor velocidade, indicada pelo verso tangente $\hat{v}$, também muda com o parâmetro tempo. Para prosseguirmos, devemos descobrir a direção da taxa de variação $\dot{\hat{v}}$ do versor tangente $\hat{v}$. Depois devemos descobrir quem é seu módulo. Um versor tem sempre seu módulo constante, unitário, mas a derivada de um versor não precisa ter um módulo constante, muito menos unitário.
- Teorema 1
- A taxa de variação $\dot{\vec{A}}$ de um vetor $\vec{A}$, de módulo $A=\|\vec{A}\|$ constante, é um vetor na direção perpendicular, \begin{equation} \label{eq:txtg} \dot{A}=0\implies \vec{A}\cdot\dot{\vec{A}}=0. \end{equation} Vale a recíproca.
A demonstração é muito simples. Basta escrever o módulo ao quadrado, por conveniência, usando a Propriedade 4 do produto escalar, e tomar a derivada desta constante, \begin{equation} \frac{d}{dt}A^{2}=2A\cdot\dot{A}=0 =\frac{d}{dt}\vec{A}\cdot\vec{A}=2\vec{A}\cdot\dot{\vec{A}}
\implies\vec{A}\cdot\dot{\vec{A}}=0. \end{equation}
Portanto, de acordo com o Teorema 1, a direção da taxa de variação $\dot{\hat{v}}$ do versor tangente $\hat{v}$ está na direção perpendicular à direção tangente. Denotemos esta direção perpendicular, melhor ainda de direção normal,
pelo versor $\hat{n}$, $\hat{v}\cdot\hat{n}=0$. Desta forma, podemos escrever \begin{equation} \label{eq:Frenet1} \dot{\hat{v}} = v\kappa\, \hat{n}, \end{equation} onde colocamos o módulo $v$ do vetor velocidade em evidência por mera conveniência e
introduzimos a função (temporal) escalar $\kappa(t)$ a ser determinada impondo que $\|\dot{\hat{v}}\| = v|\kappa|$. A análise dimensional diz que $[\hat{v}]=1$ (versores são adimensionais), $[\dot{\hat{v}}]=1/\text{T}$ e que $[v]=\text{L}/\text{T}$.
Assim $[\kappa]=1/\text{L}$. Como veremos, desejamos que a função escalar $\kappa(t)$ tenha exatamente a dimensão de inverso de comprimento.
- Teorema 2
- O vetor aceleração pode ser decomposto em duas direções perpendiculares, uma tangente ao vetor velocidade e outra normal a ele, \begin{equation} \label{eq:veca} \vec{a} = \dot{\vec{v}} = \dot{v}\,\hat{v} + v^{2}\kappa\, \hat{n}. \end{equation} A função escalar $\kappa(t)$ é conhecida por curvatura.
Como podemos calculá-la?
Exemplo. Sim, um exemplo. Seja a trajetória circular no plano $z(t)=0$ dada pela forma paramétrica \begin{equation} x(t)=R\cos\theta(t),\; y(t)=R\sin\theta(t), \end{equation} sendo $\theta$
a fase dada por \begin{equation} \theta(t)=\omega t+\varphi, \end{equation} onde $\omega$ é um parâmetro conhecido por frequência angular, $\varphi$ é a constante da fase e $R$ é o raio (igual ao comprimento do vetor posição). Então temos o vetor velocidade
\begin{equation} \begin{aligned} v_{x}&=\dot{x}=-\omega R\sin\theta=-\omega y(t),\\ v_{y}&=\dot{y}=+\omega R\cos\theta=+\omega x(t),\\ v_{z}&=\dot{z}=0, \end{aligned} \end{equation} e o vetor aceleração, \begin{equation} \begin{aligned}
a_{x}&=\dot{v}_{x}=-\omega^{2}R\cos\theta=-\omega^{2}x(t),\\ a_{y}&=\dot{v}_{y}=-\omega^{2}R\sin\theta=-\omega^{2}y(t),\\ a_{z}&=\dot{v}_{z}=0. \end{aligned} \end{equation} Note que esta aceleração é centrípeta (voltada para o centro), \begin{equation}
\vec{a}=-\omega^{2}\vec{r}=-\omega^{2}R\hat{r}=\omega^{2}R\hat{n}, \end{equation} onde introduzimos o versor $\hat{n}=-\hat{r}$, dirigido ao centro da trajetória. Comparando com o Teorema $(\ast\ast)$, temos $v^{2}\kappa=\omega^{2}R$, da qual resulta
uma curvatura constante, $\kappa=1/R$, após usarmos $v=\omega R$. Esse resultado é emblemático: a trajetória circular tem uma curvatura constante igual ao inverso de seu raio. Onde está a importância disto? Segundo os geômetras, um reta é um círculo
de raio infinito. Assim, uma reta terá uma curvatura nula. A conjectura decorrente é: curvatura pode ser usada como uma quantificação de quanto uma curva se distancia de uma reta.
Exercício 1. Determine os vetores velocidade e aceleração, e seus módulos, bem como o produto vetorial, de um objeto na trajetória no plano $z=0$ dada pela curva (círculo) na forma paramétrica
\begin{equation} x(t)=R\cos(\omega t),\quad y(t)=R\sin(\omega t), \end{equation} onde $R$ é o raio. Mostre que o vetor velocidade é sempre perpendicular ao vetor posição.
Exercício 2. Determine os vetores velocidade e aceleração, e seus módulos, bem como o produto vetorial, de um objeto na trajetória no plano $z=0$ dada pela curva (parábola) na forma paramétrica
\begin{equation} x(t)=2t,\; y(t)=3t-t^2,\; 0\leq t\leq 3/2. \end{equation} Observe o intervalo do parâmetro $t$ (tempo). Quais são o alcance e a altura máximas que esse objeto atinge? Em que respectivos tempos? Use o Sistema Internacional (SI) de unidades,
onde comprimento está em metros (m) e tempo em segundos (s).
Exercício 3. Determine os vetores velocidade e aceleração, e seus módulos, bem como o produto vetorial, de um objeto na trajetória dada pela curva (hélice) na forma paramétrica \begin{equation}
x(t)=R\cos(\omega t),\; y(t)=R\sin(\omega t),\; z(t)=t/2. \end{equation} onde $\omega$ e o raio $R$ são parâmetros arbitrários.
3.3. Curvatura
Como podemos calcular a função escalar \(\kappa(t)\), curvatura, introduzida no Teorema 2? Produto vetorial! Sim, efetue o produto vetorial entre o vetor velocidade e a aceleração escrita na forma dada no Teorema 2, \begin{equation} \vec{a} = \dot{\vec{v}}
= \dot{v}\,\hat{v} + v^{2}\kappa\, \hat{n} \implies \vec{v}\times\vec{a} = \dot{v}\,\vec{v}\times\hat{v} + v^{2}\kappa\, \vec{v}\times\hat{n}. \end{equation} Como o produto vetorial entre vetores paralelos é nulo, por definição, então $\vec{v}\times\hat{v}=0$,
resultando em \begin{equation} \vec{v}\times\vec{a} = v^{2}\kappa\, \vec{v}\times\hat{n}. \end{equation} Agora basta tomar o módulo e lembrar que $\|\vec{v}\times\hat{n}\|=\|\vec{v}\|=v$, uma vez que os vetores $\vec{v}$ e $\hat{n}$ são perpendiculares
e que $\|\hat{n}\|=1$.
- Teorema 3
- O módulo da curvatura de uma trajetória representada pelo vetor posição $\vec{r}$ (forma paramétrica) é \begin{equation} \label{eq:curv} |\kappa(t)|=\frac{\|\vec{v}\times\vec{a}\|}{v^{3}}, \end{equation} onde $\vec{v}=\dot{\vec{r}}$, $\vec{a}=\dot{\vec{v}}$ e $v=\|\vec{v}\|$.
Em geral tomamos o valor positivo para a curvatura. A curvatura é uma medida de quanto uma curva se diferencia de uma reta. Uma reta tem curvatura nula, por definição. Quanto menor o valor da curvatura, mais parecida com uma reta a curva é.
Exercício 1. Determine a curvatura da trajetória no plano $z=0$ dada pela curva (círculo) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\quad y(t)=R\sin(\omega t), \end{equation}
onde $R$ é o raio.
Exercício 2. Determine a curvatura da trajetória no plano $z=0$ dada pela curva (parábola) na forma paramétrica \begin{equation} x(t)=2t,\; y(t)=3t-t^2,\; 0\leq t\leq 3/2. \end{equation} Use
o Sistema Internacional (SI) de unidades, onde comprimento está em metros (m) e tempo em segundos (s).
Exercício 3. Determine a curvatura da trajetória dada pela curva (hélice) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\; y(t)=R\sin(\omega t),\; z(t)=t/2. \end{equation} onde
$\omega$ e o raio $R$ são parâmetros arbitrários.
3.4. Torção
Até aqui introduzimos os versores tangente \(\hat{v}\) e normal $\hat{n}$, os quais são perpendiculares. Esses dois versores formam um plano que poderá conter ou não a trajetória inteira. Trajetórias retilíneas, circulares e parabólicas estão contidas
no plano desses dois versores. Isto significa que a direção normal a esse plano, dada pela direção do versor $\hat{v}\times\hat{n}$, deve ser uma constante no tempo, ou seja, permanece sempre a mesma em todos os pontos da trajetória. Caso o versor normal
$\hat{v}\times\hat{n}$ mude ao longo da trajetória, ela não será plana. Uma trajetória elíptica não é plana. Podemos usar esses fatos para construir uma ferramenta que caracteriza se uma trajetória é plana ou não.
Seja $\hat{b}=\hat{v}\times\hat{n}$, denominado de versor binormal, o segundo versor normal ao versor tangente $\hat{v}$. Esses três versores mutuamente perpendiculares e linearmente independentes,
conhecidos por trinca (ou tríade) de Frenet, forma uma base ortonormal que muda de orientação em cada ponto da trajetória. Como são versores, a taxa de variação de um deles estará sempre na direção
perpendicular e, portanto, pode ser escrita em termos dos outros dois versores. Vimos que $\dot{\hat{v}} = v\kappa\, \hat{n}$. Quem é a taxa de variação $\dot{\hat{b}}$ da binormal? Pelo Teorema 1, esta taxa deve estar no plano dos versores $\hat{v}$
e $\hat{n}$, perpendiculares à direção binormal. Então, \begin{equation} \label{eq:dotb1} \dot{\hat{b}} = \alpha \hat{v} + \beta \hat{n}, \end{equation} onde $\alpha$ e $\beta$ são funções arbitrárias do parâmetro $t$ (tempo). Multiplicando escalarmente
esta combinação linear por $\hat{v}$ obteremos \begin{equation} \label{eq:dotb2} \dot{\hat{b}}\cdot\hat{v} = \alpha \hat{v}\cdot\hat{v} + \beta \hat{n}\cdot\hat{v}=\alpha. \end{equation}
A fim de simplificar o lado direito do resultado anterior, devemos fazer uso do teorema seguinte, válido para vetores perpendiculares. A demonstração é imediata. Basta tomar a derivada do produto escalar entre eles e igualar a zero (derivada de uma constante).
- Teorema 4
- \begin{equation} \label{eq:txvp} \vec{A}\cdot\vec{B}=0\implies \vec{A}\cdot\dot{\vec{B}}=-\dot{\vec{A}}\cdot\vec{B}. \end{equation}
Usando este teorema, a constante $\alpha$ pode ser determinada, \begin{equation} \label{eq:dotb3} \alpha=\dot{\hat{b}}\cdot\hat{v} = -\hat{b}\cdot\dot{\hat{v}}= -v\kappa\,\hat{b}\cdot\hat{n}=0. \end{equation} Portanto, \begin{equation} \label{eq:dotb}
\dot{\hat{b}} = \beta \hat{n}= -v\tau\, \hat{n}. \end{equation} Esta escolha para $\beta$ implica que a função $\kappa=\kappa(t)$ tenha a dimensão de inverso de comprimento, $[\kappa]=1/\text{L}$. Observe que esta função $\kappa$ determina se a taxa
de variação da binormal será nula ou não. Quando $\kappa=0$, então a binormal será constante, $\dot{\hat{b}}$, e a trajetória será plana. Devido à importância desta função $\kappa$ para determinarmos se uma trajetória será plana ou não, ela será denominada
de torção. A torção é uma medida de quanto uma curva se afasta de um plano.
Podemos deduzir uma expressão bastante conveniente para calcular a torção. Para isto, precisamos da derivada do vetor aceleração (decomposto nas direções tangente e normal; verifique), \begin{equation} \dot{\vec{a}} = (\ddot{v}-\kappa^{2}v^{3})\hat{v}
+ \bigl[\kappa v\dot{v} + \frac{d}{dt}(\kappa v^{2})\bigr]\hat{n}+ \kappa\tau v^{3}\hat{b}. \end{equation} Multiplicando escalarmente esta expressão por \begin{equation} \vec{v}\times\vec{a}=\vec{v}\times(\dot{v}\,\hat{v} + v^{2}\kappa\, \hat{n})=v^{2}\kappa\,
\vec{v}\times\hat{n}=v^{3}\kappa\, \hat{b},\end{equation} onde usamos os Teoremas 2 e 3, teremos (verifique) \begin{equation} \tau = \frac{\vec{v}\times\vec{a}\cdot\dot{\vec{a}}}{v^{6}\kappa^{2}}, \end{equation} ou, numa forma mais simétrica
dada no teorema seguinte.
- Teorema 5
- A torção de uma trajetória representada pelo vetor posição $\vec{r}(t)$ (forma paramétrica) é \begin{equation} \label{eq:tau} \tau(t) = \frac{\vec{v}\times\vec{a}\cdot\dot{\vec{a}}} {\|\vec{v}\times\vec{a}\|^{2}}. \end{equation}
Exercício 1. Determine a torção da trajetória no plano $z=0$ dada pela curva (círculo) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\quad y(t)=R\sin(\omega t), \end{equation} onde
$R$ é o raio.
Exercício 2. Determine a torção da trajetória no plano $z=0$ dada pela curva (parábola) na forma paramétrica \begin{equation} x(t)=2t,\; y(t)=3t-t^2,\; 0\leq t\leq 3/2. \end{equation} Use o
Sistema Internacional (SI) de unidades, onde comprimento está em metros (m) e tempo em segundos (s).
Exercício 3. Determine a torção da trajetória dada pela curva (hélice) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\; y(t)=R\sin(\omega t),\; z(t)=t/2. \end{equation} onde $\omega$
e o raio $R$ são parâmetros arbitrários.
4. Distância percorrida (Integral)
É possível calcular a distância percorrida numa trajetória a partir de sua representação paramétrica. Bom observar que em geral trajetórias são representadas por curvas espaciais exibindo curvatura e torção. Portanto, a distância percorrida numa trajetória será muito diferente da distância entre os pontos inicial e final. Uma trajetória circular ilustra bem esta situação. Suponha que um objeto realize uma volta completa numa trajetória circular. Evidentemente os pontos inicial e final serão os mesmos, implicando numa distância nula entre eles. No entanto, a distância percorrida, igual ao perímetro da trajetória circular, é maior que zero.
4.1. Estratégia
A Figura 1 ilustra a estratégia para construirmos uma ferramenta algébrica para calcular a distância percorrida (ou comprimento) \(\Delta S\) sobre uma dada trajetória $\gamma(t)$, com curvatura e torção, entre os pontos inicial $t_{i}=t_{0}$ e final
$t_{f}=t_{N}$. Estamos identificando pontos na trajetória por valores do parâmetro $t$ (tempo). Naturalmente, a distância percorrida $\Delta S$ é maior que a distância entre os pontos inicial e final dada pelo comprimento $\|\vec{R}\|$ do vetor diferença
entre estes dois pontos, $\vec{R}=\vec{r}_{f}-\vec{r}_{i}$.
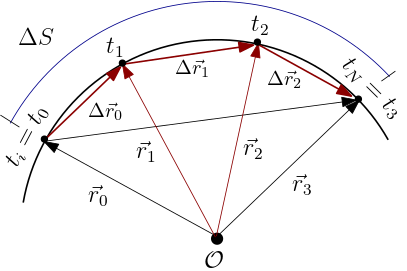
No entanto, apesar do fato $\Delta S> \|\vec{r}_{f}-\vec{r}_{i}\|$, está aí a semente de uma ideia frutífera: inserir pontos intermediários como $t_{1}$ e $t_{2}$ mostrados na Figura 1, por exemplo, e observar que a soma dos comprimentos das diferenças
sucessivas entre os vetores posição em $t_{0}$, $t_{1}$, $t_{2}$ e $t_{N}$ ($N=3$), é uma aproximação muito melhor para a distância percorrida,
onde
Note que estamos trocando a soma nos arcos (pequenos trechos na trajetória) pela soma nas cordas (comprimentos das diferenças vetoriais).
Desta forma, a soma dos comprimentos das diferenças sucessivas entre os vetores posição de $N$ pontos sobre a trajetória é uma aproximação inferior para a distância percorrida. No limite $N\to\infty$ devemos obter uma igualdade,
Como tornar este limite operacional? O que ganhamos trocando a soma nos arcos pela soma nas cordas? Ganhamos muito! O comprimento $\|\Delta\vec{r}_{j}\|$ de cada corda pode ser expresso em termos da velocidade (média),
Note que $v_{i}=v(t_{i})$ é na verdade uma velocidade média, mas será a velocidade instantânea no limite $\Delta t\to 0$. Lembre-se que $N\to\infty$ é equivalente a $\Delta t\to 0$. Assim, a distância percorrida pode ser calculada pelo limite
A nossa capacidade em executar estas somas infinitas é simplesmente incrível.
4.2. Comprimento
Por ser uma soma que envolve um processo limite e, o mais importante, que sabemos executar, daremos a ela um nome, integral, e uma notação especial.
- Teorema 1
- O comprimento de uma trajetória, ou distância percorrida entre os pontos inicial \(t_{i}\) e final $t_{f}$, é dado por \begin{equation} \label{eq:DS} \Delta S = \int_{t_{i}}^{t_{f}} v(t),\, dt\; v(t)=\|\vec{v}\|=\|\dot{\vec{r}}\|, \end{equation} onde o vetor posição $\vec{r}(t)$ representa a trajetória na forma paramétrica.
O símbolo $dt$ (denominado de diferencial) no Teorema 1 indica que a integral (soma) está sendo feita na variável $t$, a variável de integração.
A integral no Teorema 1 é denominada de definida, $t_{i}$ indicando o limite inferior e $t_{f}$ indicando o limite superior. Sem os limites de integração, uma integral é denominada de indefinida e, em geral, fornece uma nova função da variável de integração.
Pondere sobre a praticidade de ter uma ferramenta como a integral para calcular o comprimento de uma trajetória conhecendo apenas o módulo do vetor velocidade, sem a necessidade de usar uma fita métrica. Veja o Livro Apêndices para uma introdução sucinta
sobre os aspectos operacionais de integração.
Exemplo. Seja a trajetória circular no plano $z(t)=0$ dada pela forma paramétrica \begin{equation} x(t)=R\cos\theta(t),\; y(t)=R\sin\theta(t), \end{equation} sendo $\theta$ a fase dada por
\begin{equation} \theta(t)=\omega t+\varphi, \end{equation} onde $\omega$ é um parâmetro conhecido por frequência angular, $\varphi$ é a constante da fase e $R$ é o raio (igual ao comprimento do vetor posição). Então o vetor velocidade é \begin{equation}
\begin{aligned} v_{x}&=\dot{x}=-\omega R\sin\theta=-\omega y(t),\\ v_{y}&=\dot{y}=+\omega R\cos\theta=+\omega x(t),\\ v_{z}&=\dot{z}=0, \end{aligned} \end{equation} cujo módulo é \begin{equation} v(t)=\|\vec{v}\|=\sqrt{\vec{v}\cdot\vec{v}}=\omega
R. \end{equation} O tempo gasto para uma volta completa é o período $T$, tal que $\omega T=2\pi$, pois as funções trigonométricas são periódicas, $\cos\theta(t+T)=\cos\theta(t)$ (verifique). Assim, de acordo com o Teorema 1, o a distância percorrida
entre os instantes $t_{i}=0$ e $t_{f}=T$ é \begin{equation} \Delta S=\int_{0}^{T}\! v(t) dt=\omega R\int_{0}^{T}\!dt= \omega RT= 2\pi R. \end{equation} Note que este comprimento é exatamente o perímetro de uma circunferência de Raio $R$, como esperado.
Note também que este comprimento é numericamente igual à área abaixo ao gráfico da função constante $v(t)=\omega R$ no intervalo $t\in [0,T]$.
Exercício 1. Determine a distância percorrida entre os instantes $t_{i}=0$ e $t_{f}=t$ na trajetória no plano $z=0$ dada pela curva (círculo) na forma paramétrica \begin{equation} x(t)=R\cos(\omega
t),\quad y(t)=R\sin(\omega t), \end{equation} onde $R$ é o raio.
Exercício 2. Determine a distância percorrida entre os instantes $t_{i}=0$ e $t_{f}=3/2$ na trajetória no plano $z=0$ dada pela curva (parábola) na forma paramétrica \begin{equation} x(t)=2t,\;
y(t)=3t-t^2,\; 0\leq t\leq 3/2. \end{equation} Use o Sistema Internacional (SI) de unidades, onde comprimento está em metros (m) e tempo em segundos (s). Precisa de uma tabela de integrais ou, mais eficiente, de computação algébrica.
Exercício 3. Determine a distância percorrida entre os instantes $t_{i}=0$ e
$t_{f}=t$ na trajetória dada pela curva (hélice) na
forma paramétrica
\begin{equation}
x(t)=R\cos(\omega t),\; y(t)=R\sin(\omega t),\;
z(t)=t/2.
\end{equation}
onde $\omega$ e o raio $R$ são parâmetros arbitrários.
5. Computação
Apesar de vivenciarmos uma enorme popularização de diversos tipos de computadores digitais, eles são muito pouco utilizados efetivamente como partes fundamentais de nossos cursos básicos. Todo recurso humano formado em São Carlos do Pinhal deve desenvolver
suas habilidades computacionais, vitais numa sociedade moderna.
Além das linguagens computacionais tradicionais dedicadas à computação numérica, vivemos a era da maturidade da computação simbólica (ou algébrica), capaz de manipular expressões algébricas. Considerando a inexistência de cursos sobre computação algébrica,
sua importância, praticidade e disponibilidade, faremos uso dela neste curso, na medida do possível. O sistema computacional Geogebra tem se mostrado altamente adequado neste momento, pela eficiência,
disponibilidade gratuita e uma comunidade grande o suficiente capaz de facilitar o ingresso de iniciantes.
5.1. Trajetórias
Curvas espaciais representam trajetórias em Mecânica. Usaremos o Geogebra para visualizar as propriedades geométricas de algumas trajetórias. A finalidade é usar os conhecimentos adquiridos, teoricamente, para simular o movimento de algum sistema mecânico específico obedecendo as leis de Newton.
Iniciaremos pelo início: visualizar uma curva no plano (2D) contendo um ponto representando um objeto em movimento descrito pelo seu vetor posição. As taxas de variação do vetor posição serão adicionadas posteriormente. Em seguida, passaremos para curvas
no espaço (3D). Sugiro os vídeos abaixo como tutoriais.
Exercício 1. Construa no plano \(z=0\) a curva (círculo) dada pela forma paramétrica
onde o raio $R$ pode ser escolhido a vontade. Restrinja o parâmetro $t$ (tempo) ao intervalo $0\leq t\leq 2$. Mostre também um ponto na curva representando um objeto, bem como seus vetores posição, velocidade e aceleração (use uma escala conveniente). Faça uma animação mostrando este objeto em movimento sobre
esta curva.
Calcule e exiba os gráficos da curvatura e da torção.
Exercício 2. Construa no plano \(z=0\) a curva (parábola) dada pela forma paramétrica
Observe o intervalo do parâmetro $t$ (tempo). Mostre também um ponto na curva representando um objeto, bem como seus vetores posição, velocidade e aceleração (use uma escala conveniente). Faça uma animação mostrando este objeto em movimento sobre esta curva.
Calcule e exiba os gráficos da curvatura e da torção.
Exercício 3. Construa a curva (hélice) dada pela forma paramétrica
onde o raio $R$ pode ser escolhido a vontade. Restrinja o parâmetro $t$ (tempo) ao intervalo $0\leq t\leq 4$. Mostre também um ponto na curva representando um objeto, bem como seus vetores posição, velocidade e aceleração (use uma escala conveniente). Faça uma animação mostrando este objeto em movimento sobre
esta curva.
Calcule e exiba os gráficos da curvatura e da torção.
5.2. Segunda Lei
- Teorema 1
- texto