Anterior
Próximo

3. Taxas (Derivadas)

3.1. Velocidade

A taxa de variação do vetor posição é denominada de velocidade. A velocidade é um vetor e uma função do tempo \(t\). A construção desse vetor velocidade está ilustrada na Figura 1. Nesta figura, o ponto na trajetória designado por $t$ está fixo, enquanto o ponto designado por $t+\Delta t$ está livre, com $\Delta t\geq 0$.

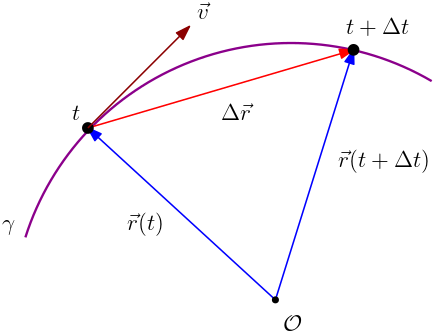
Figura 1. Definição do vetor velocidade como a primeira taxa de variação do vetor posição de um objeto em sua trajetória $\gamma$.

Seja $\Delta\vec{r}$ a diferença entre os vetores posição destes dois pontos,

\begin{equation} \label{eq:Dr} \Delta\vec{r}=\vec{r}(t+\Delta t)-\vec{r}(t). \end{equation}

Agora, num processo contínuo e suave, levemos o ponto designado por $t+\Delta t$ para as proximidades do ponto (fixo) designado por $t$. O parâmetro $t$ pode ser escolhido de tal forma que $\Delta t\to 0$ numa vizinhança muito pequena em torno do ponto designado por $t$.

Definição 1 (Velocidade)
A taxa de variação do vetor posição, ou velocidade, é uma função vetorial definida pelo processo limite \begin{equation} \label{eq:vec-v} \vec{v}(t)=\lim\limits_{\Delta t\to 0} \frac{\Delta\vec{r}}{\Delta t}\equiv \frac{d\vec{r}}{dt}\equiv \dot{\vec{r}}, \quad (\ast)\end{equation} conhecido por derivada primeira.

Designaremos as coordenadas do vetor velocidade por $v_{i}(t)$ ou $\dot{x}_{i}(t)$, com $i\in\{x,y,z\}$ ou $i\in\{1,2,3\}$, dependendo da conveniência. Reservaremos o ponto (e somente o ponto) sobre o nome para representar a primeira derivada temporal (e somente a derivada temporal, i.e., em relação ao tempo $t$, $dx/dt=\dot{x}$). Veja o Cap. 2 do Livro Apêndices para um guia sobre derivadas para iniciantes.

Interpretação geométrica. A interpretação geométrica do vetor velocidade está na Figura 1. Antes do processo limite $\Delta t\to 0$, a direção do vetor diferença $\Delta\vec{r}$ é uma reta secante, i.e., ela passa por dois pontos na trajetória. Após processo limite $\Delta t\to 0$, a direção do vetor velocidade é uma reta tangente, pois tem apenas um ponto de contato com a curva $\gamma$ que representa a trajetória. A direção tangente definida por esse processo é única. A direção do vetor velocidade é tangente à trajetória. Assim, devemos sempre colocar o vetor velocidade iniciando na posição do objeto e na direção tangente à trajetória, como mostrado na Figura 1. Bom lembrar que o vetor posição inicia sempre na origem do sistema de coordenadas (ponto $\mathcal{O}$).

Análise dimensional. Veja o Cap. 1 do Livro Apêndices para uma introdução à Análise Dimensional. Uma análise dimensional do vetor velocidade mostra que suas dimensões são as mesmas de comprimento por tempo, $[\vec{v}]=[dx/dt]=\text{L}/\text{T}$. Note que estamos tratando as diferenciais $dx$ e $dt$ como quantidades (infinitesimalmente pequenas) com as dimensões de comprimento e tempo, respectivamente. Lembre sempre que velocidade é um vetor, por definição, com dimensões de comprimento por tempo. Livre-se da concepção adquirida que velocidade é "espaço por tempo", a qual contém dois erros graves: velocidade não é um escalar (espaço) e "espaço" é muito mais que o comprimento entre dois pontos num espaço. Usar "espaço percorrido por tempo gasto" não ajuda muito, mesmo se interpretar "espaço percorrido" como a distância percorrida ou comprimento do trajeto. Velocidade é um vetor, por definição, e, como tal, deve ser grafado (com a flecha).

Rapidez. Denominaremos por rapidez o módulo do vetor velocidade,

\begin{equation} \label{eq:rap} v(t)=\|\vec{v}(t)\|=\sqrt{\vec{v}\cdot\vec{v}}=\sqrt{v_{x}^{2}(t)+v_{y}^{2}(t)+v_{z}^{2}(t)}. \end{equation}

Note que estamos usando a Propriedade 4 do produto escalar numa base ortonormal. Note também que a rapidez é um escalar, diferentemente da velocidade (um vetor). Veremos que a rapidez terá um papel importante no cômputo do comprimento de um trajeto.

Exemplo. Sim, um exemplo. Seja a trajetória circular no plano $z(t)=0$ dada pela forma paramétrica

\begin{equation} x(t)=R\cos\theta(t),\; y(t)=R\sin\theta(t), \end{equation}

sendo $\theta$ a fase dada por

\begin{equation} \theta(t)=\omega t+\varphi, \end{equation}

onde $\omega$ é um parâmetro conhecido por frequência angular, $\varphi$ é a constante da fase e $R$ é o raio (igual ao comprimento do vetor posição). Então a Definição 1 nos permite calcular o vetor velocidade

\begin{equation} \vec{v}=\dot{\vec{r}}=(\dot{x},\dot{y},\dot{z})=(v_{x},v_{y},v_{z}). \end{equation}

Efetuando as derivadas temporais, teremos

\begin{equation} \begin{aligned} v_{x}&=\dot{x}=\dot{\theta}(-R\sin\theta)=-\omega R\sin\theta,\\ v_{y}&=\dot{y}=\dot{\theta}(+R\cos\theta)=+\omega R\cos\theta,\\ v_{z}&=\dot{z}=0. \end{aligned} \end{equation}

Esse vetor velocidade tem algumas características interessantes. Ele é perpendicular ao vetor posição, $\vec{r}\cdot\vec{v}=0$, e seu módulo é constante, $v=\|\vec{v}\|=\omega R$. Resultado conhecido? Agora sabe de onde veio. Verifique. Sempre que obtiver resultados algébricos, como esses, use análise dimensional para checar a consistência de seus resultados. Quais são as dimensões do parâmetro $\omega$? Como a fase (argumento de uma função trigonométrica) deve ser adimensional, então a dimensão da frequência angular $\omega$ deve ser inverso de tempo, $[\omega]=1/\text{T}$. Desta forma, tanto a velocidade quanto a rapidez estão com as dimensões corretas, $[v]=[\omega R]=\text{L}/\text{T}$.

Exercício 1. Determine o vetor velocidade, e seu módulo, de um objeto na trajetória no plano $z=0$ dada pela curva (círculo) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\quad y(t)=R\sin(\omega t), \end{equation} onde $R$ é o raio. Mostre que o vetor velocidade é sempre perpendicular ao vetor posição.

Exercício 2. Determine o vetor velocidade, e seu módulo, de um objeto na trajetória no plano $z=0$ dada pela curva (parábola) na forma paramétrica \begin{equation} x(t)=2t,\; y(t)=3t-t^2,\; 0\leq t\leq 3/2. \end{equation} Observe o intervalo do parâmetro $t$ (tempo). Quais são o alcance e a altura máximas que esse objeto atinge? Em que respectivos tempos? Use o Sistema Internacional (SI) de unidades, onde comprimento está em metros (m) e tempo em segundos (s).

Exercício 3. Determine o vetor velocidade, e seu módulo, de um objeto na trajetória dada pela curva (hélice) na forma paramétrica \begin{equation} x(t)=R\cos(\omega t),\; y(t)=R\sin(\omega t),\; z(t)=t/2. \end{equation} onde $\omega$ e o raio $R$ são parâmetros arbitrários.


Anterior
Próximo