Anterior
Próximo

2. Geometria

2.6. Produto misto

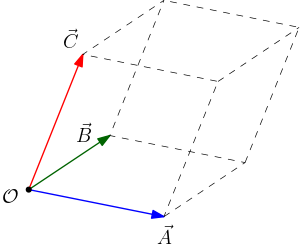
O produto misto envolve um produto vetorial seguido de um produto escalar, nessa ordem.  A sua definição é: dado três vetores \(\vec{A}\), $\vec{B}$ e $\vec{C}$ quaisquer, o produto misto é um número definido por $\vec{C}\cdot(\vec{A}\times\vec{B})$ (veja a Figura 1). Note que temos de executar primeiro o produto vetorial $\vec{A}\times\vec{B}$, o qual resultará em um vetor, para depois calcularmos o produto escalar com $\vec{C}$, resultando em um número. Que acontece se as posições dos três vetores no produto misto $\vec{C}\cdot(\vec{A}\times\vec{B})$ forem modificadas simultaneamente, por exemplo para $\vec{B}\cdot(\vec{C}\times\vec{A})$?  Nada! O produto misto é invariante por permutações circulares (cíclicas) das letras $A$, $B$ e $C$,

Teorema 6
O produto misto é invariante por permutações circulares (cíclicas), \begin{equation} \vec{A}\cdot(\vec{B}\times\vec{C}) = \vec{C}\cdot(\vec{A}\times\vec{B}) = \vec{B}\cdot(\vec{C}\times\vec{A}). \end{equation}

Uma forma de provar esta propriedade é fazendo uso do determinante para calcular o produto vetorial (verifique):

\begin{equation} \label{eq:prodmistodet} \vec{A}\cdot(\vec{B}\times\vec{C}) = \vec{A}\cdot \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ B_{x} & B_{y} & B_{z}\\ C_{x} & C_{y} & C_{z} \end{vmatrix} = \begin{vmatrix} A_{x} & A_{y} & A_{z}\\ B_{x} & B_{y} & B_{z}\\ C_{x} & C_{y} & C_{z} \end{vmatrix}. \end{equation}

Note que as permutações cíclicas efetuadas no produto misto correspondem a quatro trocas de linhas no último determinante, deixando-o inalterado. Portanto, do ponto de vista operacional, o produto misto está muito bem compreendido.

E o significado geométrico do produto misto? Muito bem, você está aprendendo rápido as regras do nosso jogo. O produto misto é numericamente igual ao volume do paralelepípedo formado pelos três vetores $\vec{A}$, $\vec{B}$ e $\vec{C}$ conforme ilustrado pela Figura 1. Acompanhe a demonstração trabalhando o Exercício 2.

Exercício 1. Trabalhe detalhadamente todas as situações especificadas por "Verifique".

Exercício 2. Calcule o produto misto entre os vetores posição $\vec{A}=(1,2,1)$, $\vec{B}=(1,1,2)$ e $\vec{C}=(1,1,-1)$ mostrados na Figura 1. Calcule também os ângulos entre esses vetores e seus comprimentos.

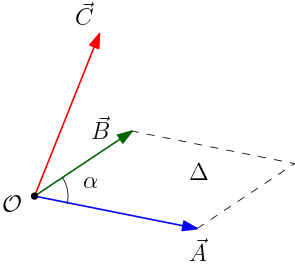
Exercício 3. Prove a propriedade geométrica do produto misto. Resolução. O volume de uma paralelepípedo é igual ao produto da área de uma de suas faces pela altura (perpendicular à face escolhida). Implemente esta estratégia com os passos seguintes.

  1. Calcule a área $\Delta$ da face formada pelos  vetores $\vec{A}$ e $\vec{B}$: $\Delta=||\vec{A}\times\vec{B}||=AB\,\mathrm{sen}\,\alpha$, onde $A=||\vec{A}||$ e $B=||\vec{B}||$ (veja a Figura 2).
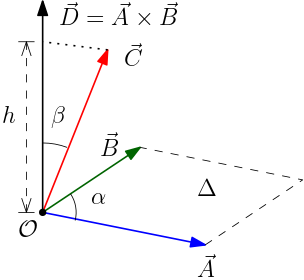
  2. Calcule a altura $h$ projetando o vetor $\vec{C}$ na direção perpendicular a plano dos vetores $A$ e $B$: $h=\vec{C}\cdot\hat{D}=C\,\mathrm{cos}\,\beta$ com $\hat{D}=\vec{A}\times\vec{B}/||\vec{A}\times\vec{B}||$ e $C=||\vec{C}||$ (veja a Figura 3).
  3. Portanto, o volume $v$ do paralelepípedo é $v=ABC\,\mathrm{sen}\,\alpha\,\mathrm{cos}\,\beta= \vec{C}\cdot(\vec{A}\times\vec{B})$. Verifique numericamente esta primeira igualdade usando os dados do Exercício 2.
Tabela 1.
Figura 1.
Figura 2.
Figura 3.



Anterior
Próximo