Física Básica I

Definição. Há somente mais uma operação binária com vetores que nos interessa (e muito). Desta vez, esta operação binária produzirá um novo vetor. Seja \(\mathbb{V}\) o conjunto de todos os vetores. Esta nova operação binária entre os vetores $\vec{A}$ e $\vec{B}$, denotada por $\vec{A}\times\vec{B}\in \mathbb{V}$, será denominada de produto vetorial. Lembre-se que o produto escalar produz um número real (escalar) e o produto vetorial produz um vetor (flecha). O produto vetorial é definido requerendo que ele satisfaça as propriedades seguintes.

1. Anti-simetria: $\displaystyle \vec{A}\times\vec{B}=-\vec{B}\times\vec{A}$.
2. Linearidade: $\displaystyle\vec{C}\times(\alpha\vec{A}+\beta\vec{B})=\alpha(\vec{C}\times\vec{A})+\beta(\vec{C}\times\vec{B}),\; \alpha,\beta\in \mathbb{R}$.
3. Perpendicularidade: $\displaystyle\vec{C}\equiv\vec{A}\times\vec{B}\implies\vec{C}\cdot\vec{A}=\vec{C}\cdot\vec{B}=0$
4. Orientabilidade: $\displaystyle (\vec{A},\vec{B},\vec{C})\leftrightarrow (\hat{\imath},\hat{\jmath},\hat{k}),\; \vec{C}\equiv\vec{A}\times\vec{B}$.

A propriedade 1 afirma que o produto vetorial, ao contrário do produto escalar, é anti-simétrico (troca de sinal quando os vetores trocam de posições). A propriedade 2 significa que o produto vetorial, assim como o produto escalar, é linear. Note que os escalares $\alpha$ e $\beta$ no lado direito podem ser retirados de dentro do produto vetorial (como no caso do produto escalar). A propriedade 3 significa que o vetor resultante $\vec{A}\times\vec{B}$ é, simultaneamente, perpendicular aos vetores $\vec{A}$ e $\vec{B}$.

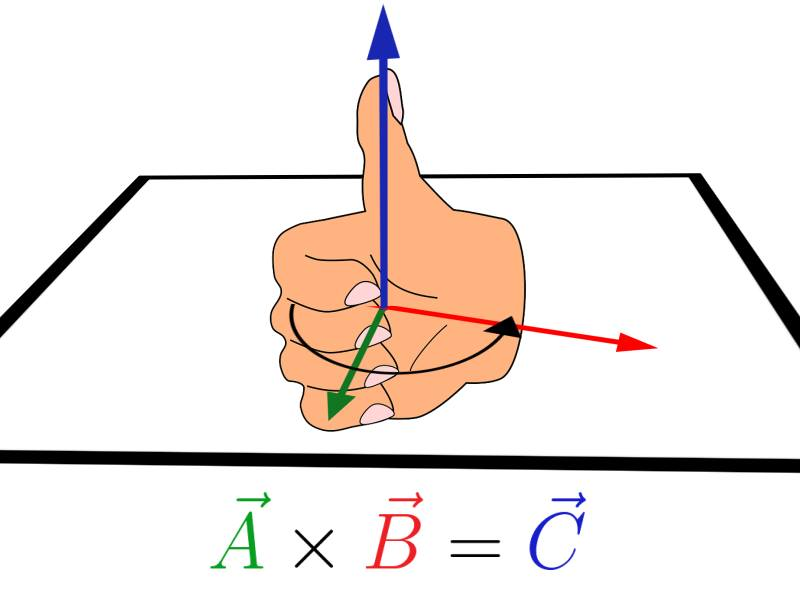
A propriedade 4 é uma novidade. O produto vetorial cria um vetor numa direção e que precisa de um sentido nesta direção. A propriedade 4 afirma que o sentido do vetor resultante $\vec{C}=\vec{A}\times\vec{B}$ na trinca $(\vec{A},\vec{B},\vec{A}\times\vec{B})$ é idêntico ao sentido do versor $\hat{k}$ na trinca de versores $(\hat{\imath},\hat{\jmath},\hat{k})$ de um referencial ortonormal. É equivalente à regra da mão direita indicada na Figura 1: o sentido do vetor resultante $\vec{C}=\vec{A}\times\vec{B}$ é indicado pelo nosso polegar direito quando movimentamos os demais dedos da mão direita no sentido de $\vec{A}$ para $\vec{B}$. Note que a propriedade 4 é uma escolha para a orientação do produto vetorial (estamos usando a regra da mão direita para estabelecer uma orientação espacial).

Teoremas. Como podemos calcular as componentes do vetor resultante $\vec{C}=\vec{A}\times\vec{B}$ a partir das componentes dos vetores $\vec{A}=(A_{x},A_{y},A_{z})$ e $\vec{B}=(B_{x},B_{y},B_{z})$? Isto pode ser feito em duas etapas. Primeiro observe que a propriedade 3 nos fornece as seguintes relações (verifique):

Note que estamos pressupondo que estes vetores estejam decompostos numa base ortonormal. Caso a base não seja ortonormal, devemos efetuar os produtos escalares usando a métrica apropriada. Destas relações, podemos escrever, por exemplo, as componentes $C_{x}$ e $C_{y}$ em função de $C_{z}$ (verifique),

Naturalmente, podemos reescrevê-las na forma (verifique)

onde $\beta$ é um número real arbitrário  e independente das coordenadas dos vetores $\vec{A}$ e $\vec{B}$.  Estas razões devem ser válidas para quaisquer vetores $\vec{A}$ e $\vec{B}$. Desta forma, temos as componentes do vetor $\vec{C}$, resultante do produto vetorial $\vec{A}\times\vec{B}$, em termos das componentes dos vetores $\vec{A}$ e $\vec{B}$ e da constante arbitrária $\beta$. Mas como esta constante $\beta$ é arbitrária, então podemos escolher um valor para ela: $\beta=1$. Não se assuste, como veremos adiante, há várias razões práticas para tal escolha. Com $\beta=1$, temos mais um teorema.

Teorema 4

As componentes (base ortonormal) do produto vetorial $\vec{C}=\vec{A}\times\vec{B}$ são: \begin{equation} C_{x}=A_{y}B_{z}-A_{z}B_{y},\; C_{y}=A_{z}B_{x}-A_{x}B_{z},\; C_{z}=A_{x}B_{y}-A_{y}B_{x}. \end{equation}

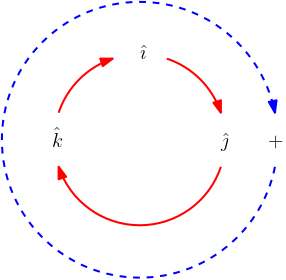
Como veremos através de vários exemplos, escolher $\beta$ como sendo um número positivo está condizente com a propriedade 4 (regra da mão direita) do produto vetorial. Caso tivéssemos escolhido um número negativo para $\beta$, teríamos que usar uma regra da mão esquerda. Note que a disposição dos índices $x$, $y$ e $z$ nas expressões dadas no Teorema 4 segue uma ordem cíclica, com valores positivos no sentido horário, $\{(x,y,z),(z,x,y),(y,z,x)\}$, e com valores negativos no sentido anti-horário, $\{(x,z,y),(y,x,z),(z,y,x)\}$. Veja a Figura 2, com $(\hat{\imath},\hat{\jmath},\hat{k})$ trocados por $(x,y,z)$, para uma ilustração de mais uma regra mnemônica.

Tendo as componentes do vetor $\vec{C}$, oriundo do produto vetorial $\vec{A}\times\vec{B}$, podemos calcular seu módulo  usando o produto escalar.  Após um pouco de paciência, encontraremos (verifique)

a qual pode ser perfeitamente reescrita, usando o Teorema 2, em termos do ângulo $\theta$ entre $\vec{A}$ e $\vec{B}$,

Portanto, temos outro teorema.

Teorema 5

O módulo do vetor $\vec{C}= \vec{A}\times\vec{B}$ pode ser convenientemente calculado por $\displaystyle C=AB\,|\!\sin\theta|$.

Este teorema nos permite calcular o comprimento do vetor resultante de um produto vetorial a partir dos comprimentos dos vetores iniciais e do ângulo entre eles, sem a necessidade de escrevê-los em um sistema de coordenadas. Esta situação é análoga àquela relacionada com o Teorema 2.

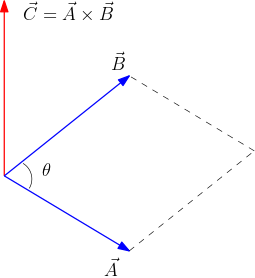
Significado geométrico. Vimos anteriormente que um produto escalar está associado com a projeção de um vetor sobre o outro. E o produto vetorial?  ele tem alguma interpretação geométrica?  Sim, ele tem e é muito relevante.  Note que a expressão $AB\,|\!\sin\theta|$ é numericamente igual à área do paralelogramo de lados $A=||\vec{A}||$ e $B=||\vec{B}||$, formado pelos vetores $\vec{A}$ e $\vec{B}$ (veja a Figura 3 para se convencer disto).  Note que a escolha $\beta=1$ permite esta interpretação.  Caso contrário ($\beta\neq 1$), teríamos a área do paralelogramo multiplicada pelo valor de $\beta$. Desta forma, podemos adotar esta interpretação geométrica como mais uma propriedade na definição do produto vetorial (para fixar o valor $\beta=1$).  Esta propriedade geométrica será usada para derivarmos uma das leis de Kepler para o movimento planetário.

Vejamos outras consequências do Teorema 4.  A propriedade 5 significa que o produto vetorial entre dois vetores paralelos (ou anti-paralelos) resulta em um vetor nulo, pois neste caso o ângulo entre eles é 0 graus (ou 180 graus). Esta propriedade, juntamente com a regra da mão direita nos permite calcular todos os produtos vetoriais entre os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ de uma base ortonormal:

Notas.

1. Observando os produtos vetoriais entre os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, percebemos que a regra da mão direita é equivalente a efetuarmos permutações circulares nos versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, tomando o sentido horário como positivo, como indicado na Figura 2.
2. A escolha $\beta=1$ no cálculo das componentes do produto vetorial garante que o versor resultante $\hat{\imath} = \hat{\jmath}\times\hat{k}$ seja unitário.
3. Usando os produtos vetoriais entre os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ e a propriedade de linearidade, podemos calcular o produto vetorial entre dois vetores arbitrários escritos explicitamente em termos de uma base ortonormal.
4. Mencionamos anteriormente que um pseudo-vetor não inverte o seu sentido perante uma inversão espacial. Sendo assim, um produto vetorial é um pseudo-vetor, pois invertendo os sentidos de $\vec{A}$ e $\vec{B}$, simultaneamente, em $\vec{A}\times\vec{B}$ nada de novo acontece. Em Física, temos vários pseudo-vetores importantes. Iremos trabalhar com dois deles em Mecânica: momentum angular $\vec{L}=\vec{r}\times\vec{p}$ e torque $\vec{\tau}=\vec{r}\times\vec{F}$, onde $\vec{r}$ é o vetor posição, $\vec{p}$ é o momentum linear ($\vec{p}=m\vec{v}$) e $\vec{F}$ é a força resultante atuando no centro de massa de um objeto de massa $m$. Nas nossas aplicações iremos usar também a força de Lorentz, outro pseudo-vetor importante, $\vec{F}_{L}=q\,\vec{v}\times\vec{B}$, produzida por um campo magnético $\vec{B}$ sobre uma carga $q$ em movimento com uma velocidade $\vec{v}$.
   

Exercício 1. Trabalhe detalhadamente todas as situações especificadas por "Verifique".

Exercício 2. Efetue o produto vetorial $\vec{R}_{3}=\vec{R}_{1}\times\vec{R}_{2}$ entre os vetores posição $\vec{R}_{1}=(1,2,1)$ e $\vec{R}_{2}=(1,1,2)$. Calcule os comprimentos de cada vetor, bem como os ângulos entre eles. Faça uma representação gráfica destes vetores. Calcule também a área de cada paralelogramo formado por cada par de vetores. Considere um sistema ortonormal de coordenadas. 

Exercício 3. Verifique que as componentes do vetor resultante de um produto vetorial também podem ser calculadas através do determinante

Exercício 4. Usando coordendas, verifique a identidade (muito útil) $\vec{A}\times(\vec{B}\times\vec{C})= \alpha\vec{B}-\beta\vec{C}$, onde $\alpha=\vec{A}\cdot\vec{C}$ e $\beta=\vec{A}\cdot\vec{B}$. Note que não uma componente na direção do vetor $\vec{B}$.

Tabela 1.

Figura 1. Regra da mão direita.	Figura 2. Regra cíclica.	Figura 3. Paralelogramo.