Física Básica I

Há outras operações binárias que podemos realizar com vetores, além da combinação linear? É possível inventar uma operação entre dois vetores que nos dê informações sobre seus comprimentos e o ângulo entre eles? Sim, é possível e muito útil. Vejamos.

Podemos construir uma operação binária envolvendo dois vetores cujo resultado é um número real. Esta operação binária entre os vetores \(\vec{A}\) e $\vec{B}$, denotada por $\vec{A}\cdot\vec{B}\in \mathbb{R}$, será denominada de produto escalar. O produto escalar é definido requerendo que ele satisfaça as propriedades seguintes.

1. Simetria: $\displaystyle \vec{A}\cdot\vec{B} = \vec{B}\cdot\vec{A}\in \mathbb{R}$.
2. Linearidade:$\displaystyle \vec{C}\cdot(\alpha\vec{A}+\beta\vec{B})= \alpha\,\vec{C}\cdot\vec{A} + \beta\,\vec{C}\cdot\vec{B},\; \alpha,\beta\in \mathbb{R}$.
   
3. Positivo definido: $\displaystyle \vec{A}\cdot\vec{A}=0\iff\vec{A}=\vec{0},\; \vec{A}\cdot\vec{A}>0\iff\vec{A}\ne\vec{0}$.
4. Mensurabilidade: $\displaystyle A\equiv||\vec{A}||\equiv\sqrt{\vec{A}\cdot\vec{A}}$.

A propriedade 1 expressa que o produto escalar é uma operação binária simétrica (ou comutativa). A propriedade 2 significa que o produto escalar é linear, pois obedece a propriedade distributiva. Note que os números $\alpha$ e $\beta$ podem ser retirados livremente de dentro do produto escalar. A propriedade 3 garante que o produto escalar seja bem comportado (não-degenerado), pois evita que o produto escalar de um vetor com ele mesmo seja nulo sem que o vetor seja nulo. A propriedade 4 garante que o comprimento, também conhecido por módulo ou norma, seja calculado pelo produto escalar. Note que a propriedade 3 está em sintonia com a definição de comprimento como uma quantidade real positiva ou nula. Comprimento nulo quando, e somente quando, o vetor for nulo. O produto escalar é um instrumento (analítico) de medida do comprimento de um vetor.

Uma questão importante é: como realizar esta operação binária, denominada de produto escalar, em termos de coordenadas? ou seja, como tornar o produto escalar operacional? Graças à propriedade distributiva 2, basta conhecermos todos os produtos escalares possíveis entres os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, colocados ao longo dos três eixos independentes do espaço euclidiano (veja a Figura 1). Desta forma, teremos, em princípio, nove produtos escalares a serem determinados, pois cada vetor pode ser escrito como uma combinação linear dos versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ do sistema de coordenadas escolhido. No entanto, a propriedade de simetria, reduz para seis o número de produtos escalares que devemos conhecer. Uma forma eficiente de guardarmos estes produtos escalares é utilizando um arranjo matricial, isto é, uma matriz $3\times 3$,

Esta matriz é denominada de métrica (por razões óbvias). É sempre bom procurarmos por expressões matemáticas mais sintéticas. Simplesmente rebatizando os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ para

podemos reescrever os elementos de matriz da métrica como (verifique)

Além de mais simples é também muito elegante. Note que a simetria da métrica é uma consequência direta da simetria do produto escalar.

Considere agora dois vetores escritos num mesmo referencial, como aquele mostrado na Figura 1, com os versores escritos como acima, em termos de $\hat{e}_{i}$. Seja então

Agora use todas as propriedades do produto escalar para calcular explicitamente, de preferência usando os somatórios,

Note o uso de índices distintos ($i$ e $j$) no momento de escrever cada um dos vetores em coordenadas. Cada soma requer um índice distinto. Não economize nos índices. Este mesmo resultado pode ser reobtido usando produtos matriciais (linhas por colunas). Basta usar o vetor $\vec{A}=(A_{i})=(A_{1},A_{2},A_{3})$ como uma matriz linha $(A_{j})$ e o vetor $\vec{B}$ como uma matriz coluna (a transposta), $(B_{j})^{\textrm{T}}$.

Teorema 1

Sejam $\vec{A}$ e $\vec{B}$ dois vetores descritos numa base qualquer dada pela métrica $g$. Então, o produto escalar entre eles é \begin{equation} \vec{A}\cdot\vec{B} = (A_{i})\, g\, (B_{j})^{\textrm{T}}. \end{equation}

Afinal de contas, como poderemos calcular os produtos escalares que aparecem na métrica? Não podemos! Estes produtos escalares devem ser fornecidos no momento em que compramos o referencial. Para entendermos melhor esta situação, devemos nos perguntar: qual é o significado geométrico do produto escalar?

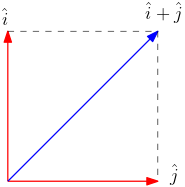
Para entendermos melhor o significado geométrico do produto escalar, devemos calcular primeiro o produto escalar entre dois vetores perpendiculares (ortogonais). Vamos usar os versores $\hat{\imath}$ e $\hat{\jmath}$ como dois representantes típicos de vetores ortogonais. Como indicado na Figura 2, o comprimento da soma vetorial $\hat{\imath} + \hat{\jmath}$ é a hipotenusa do triângulo retângulo formado pelos versores $\hat{\imath}$ e $\hat{\jmath}$. Como os versores possuem comprimentos unitários, por definição, então a hipotenusa pode ser calculada usando o teorema de Pitágoras,

Sim, você tem razão. Naturalmente, o valor da hipotenusa também pode ser calculado usando o produto escalar para calcular o comprimento de um vetor,

onde usamos também a propriedade distributiva do produto escalar. Comparando estes dois resultados, concluímos que $\hat{\imath}\cdot\hat{\jmath}=0$. Isto significa que o produto escalar entre dois vetores ortogonais é nulo. Este resultado continua valendo mesmo para vetores não-unitários, seguindo o mesmo raciocínio anterior. Portanto ele é um teorema:

Teorema 2

Sejam $\vec{A}$ e $\vec{B}$ dois vetores perpendiculares. Então, $\displaystyle\vec{A}\cdot\vec{B}=0\quad\iff \quad \vec{A}\perp\vec{B}$.

Portanto, sabemos o significado de cada elemento na diagonal da métrica: são os comprimentos (ao quadrado) dos versores. Para o sistema de coordenadas cartesiano da Figura 1, os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ são unitários (possuem comprimentos iguais a um).

E quando os vetores não são perpendiculares? qual é o significado do produto escalar? Considere dois vetores arbitrários $\vec{A}$ e $\vec{B}$, formando um ângulo $\theta$ entre eles. Dois vetores sempre estão em um plano, como mostrado na Figura 3. Escolha neste plano um vetor $\vec{C}$ perpendicular a $\vec{B}$. Naturalmente, os versores $\hat{B}$ e $\hat{C}$ formam uma base ortonormal para o vetor $\vec{A}$, isto é, podemos escrever $\vec{A} = A\cos\theta\,\hat{B} + A\sin\theta\,\hat{C}$. Efetue agora o produto escalar $\vec{A}\cdot\hat{B}$ e use o Teorema 1. Resulta (verifique) que $A\cos\theta= \vec{A}\cdot\hat{B}$. O produto escalar $\vec{A}\cdot\hat{B}$ é exatamente a projeção do vetor $\vec{A}$ sobre o versor $\hat{B}$ (ou na direção do vetor $\vec{B}$). Note na Figura 1 que $\vec{r}\cdot\hat{\imath}=x$, $\vec{r}\cdot\hat{\jmath}=y$ e $\vec{r}\cdot\hat{k}=z$, ou seja, as coordenadas são as projeções do vetor sobre os versores da base. Naturalmente, os papeis de $\vec{A}$ e $\vec{B}$ podem ser perfeitamente invertidos. Assim, temos um segundo teorema.

Teorema 3

Sejam $\vec{A}$ e $\vec{B}$ dois vetores formando um ângulo $\theta$ entre eles. Então, $\displaystyle \vec{A}\cdot\vec{B}=AB\cos\theta$.

Note que este teorema nos permite calcular o produto escalar entre dois vetores sem a necessidade de escrevê-los em um determinado sistema de coordenadas, basta conhecermos seus comprimentos e o ângulo entre eles. Vetores são flechas e existem independentemente de um referencial (sistema de coordenadas).

Resumindo: além do comprimento, o produto escalar nos dá também uma informação sobre a orientação relativa entre vetores. Também é importante notar que o Teorema 2 nos fornece uma forma operacional para calcularmos o produto escalar entre vetores quando seus comprimentos e o ângulo entre eles são conhecidos previamente.

Voltemos ao nosso problema original: o sistema cartesiano da Figura 1. Nele, escolhemos os três versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ mutuamente ortogonais (perpendiculares), isto é, os ângulos entre estes versores é de 90 graus. Portanto, usando o Teorema 1, a métrica desse sistema de coordenadas é

ou seja, ela é a matriz identidade para um sistema de coordenadas ortonormal. Isto simplifica muito nossa vida e explica a importância prática de usarmos sistemas ortonormais (versores ortogonais e unitários) de coordenadas.  Assim, podemos escrever o produto escalar entre dois vetores arbitrários $\vec{A}=(A_{x},A_{y},A_{z})$ e $\vec{B}=(B_{x},B_{y},B_{z})$, em um sistema de coordenadas ortonormal cartesiano simplesmente multiplicando componentes na mesma direção e somando (verifique)

Como mais um teste de consistência, use $(\ast)$ para calcular o comprimento do vetor posição $\vec{r}$ da Figura 1 e veja que é o mesmo valor obtido diretamente das projeções indicadas na mesma figura.

Também é importante ter em mente que a expressão $(\ast)$ é válida somente em um sistema ortonormal de coordenadas. Caso a base não seja ortonormal, devemos usar a métrica apropriada em todas as operações envolvendo o produto escalar. Também devemos ter em mente que a métrica vem junto com a base, ela é um conjunto de ``especificações técnicas'' sobre a base, uma espécie de ``manual de instruções''. Se alguém lhe vender uma base sem a métrica, entre em contato com o Procon mais próximo.

Uma vez que as coordenadas dos vetores $\vec{A}$ e $\vec{B}$ são conhecidas em um sistema ortonormal de coordenadas, então podemos usar $(\ast)$ para calcular (em termos das coordenadas) o valor do produto escalar que aparece no lado esquerdo do Teorema 2, bem como os módulos $A$ e $B$ que aparecem no lado direito. Assim, poderemos usar o Teorema 2 para calcular o ângulo entre dois vetores.

Exercício 1. Trabalhe detalhadamente todas as situações especificadas por "Verifique".

Exercício 2. Efetue o produto escalar entre os vetores posição $\vec{R}_{1}=(1,2,1)$ e $\vec{R}_{2}=(1,1,2)$. Calcule também o comprimento de cada um deles bem como o ângulo entre eles. Repita este procedimento para os vetores resultantes da soma e da diferença entre $\vec{R}_{1}$ e $\vec{R}_{2}$. Considere um sistema ortonormal de coordenadas.

Exercício 3. Suponha que uma determinada base tenha a seguinte métrica:

Determine os ângulos entre os versores desta base e desenhe-a. Suponha que $\vec{R}_{1}=(1,2,1)$ e $\vec{R}_{2}=(1,1,2)$ sejam dois vetores escritos nesta base. Determine seus comprimentos e o produto escalar e o ângulo entre eles. Desenhe-os nesta base.

Tabela 1.

Figura 1. Referencial ortonormal.	Figura 2. Teorema 1.	Figura 2. Teorema 2.