Física Básica I

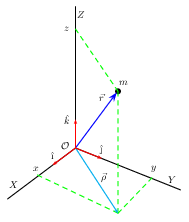
Um vetor com a origem fixa na origem de um sistema de coordenadas e com a ponta na posição de um objeto (em movimento ou não) é denominado de vetor posição. Como exemplo, veja o vetor \(\vec{r}\) na Figura 1. Essencialmente, estamos usando vetores para representar posições. Em princípio não precisamos usar um vetor para localizar um ponto no espaço. No entanto, a noção de velocidade requer a presença de um vetor posição, como veremos adiante. Quando há movimento, é importante especificar também a direção e o sentido deste movimento. Em outras palavras, precisamos saber para onde estamos indo, literalmente. Como veremos, vetores constituem uma linguagem matemática extremamente concisa, elegante e prática para descrevermos posições, velocidades, acelerações e outras quantidades físicas, como forças, que necessitam de direção e sentido, além de intensidade, para serem especificadas completamente.

Vejamos então algumas propriedades importantes sobre vetores. Primeiro, vetores podem ser multiplicados por números, mantendo a direção e alterando o comprimento. O sentido será invertido somente se esse número for negativo. Segundo, vetores podem ser somados (ou subtraídos) de acordo com a regra simples: a soma é nula se os vetores formarem um polígono fechado, com a ponta de um vetor no "pé'' do outro, como ilustrado na Figura 2 onde $\vec{A}+\vec{B}+\vec{C}=0$. Note que estamos assumindo que vetores possam ser transportados (como flechas) sem que haja mudanças no comprimento, direção e sentido. Quando multiplicamos objetos por números e realizamos somas desses mesmos objetos, obtendo objetos do mesmo tipo, estamos realizando combinações lineares. Por exemplo, na Figura 2 podemos formar a combinação linear $\vec{C}=-\vec{A}-\vec{B}$, entre outras possíveis.

Outra característica de um vetor, muito importante para a Física, é o seu comportamento em relação a rotações em torno de um eixo fixo e à inversões espaciais. Quando um vetor é rodado em torno de um eixo fixo, o comprimento do vetor não é alterado. Inversão espacial significa inverter o sentido, mantendo a direção e o comprimento inalterados ("virar ao avesso''). Um candidato a vetor (que tem comprimento, direção e sentido) que permanece invariante a uma inversão espacial é denominado de pseudo-vetor.

A descrição de vetores num sistema de coordenadas é muito frutífera. Vamos denotar por $\hat{r}$ (observe a notação) um vetor de comprimento unitário, o qual chamaremos de versor. O versor sempre indica a direção e o sentido de um determinado vetor. Sendo $r$ o comprimento do vetor $\vec{r}$, então $\vec{r}=r\hat{r}$, sempre. A Figura 1 exibe três versores, $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$: um versor para cada uma das três direções independentes. Observe na Figura 1 que podemos formar, naturalmente, a combinação linear $\vec{\rho} = x\hat{\imath} + y\hat{\jmath}$, bem como $\vec{r}= \vec{\rho} + z\hat{k}$. Portanto,

onde a notação $\vec{r}=(x,y,z)$ é conveniente (a ordem não pode ser alterada). As projeções $(x,y,z)$ são as coordenadas do vetor posição $r$ no sistema de coordenadas $\mathcal{O}$. Por exemplo, quando escritos nesta notação conveniente, a combinação linear entre os vetores $\vec{A}=(x_{a},y_{a},z_{a})$ e $\vec{B}=(x_{b},y_{b},z_{b})$ será

Vale observar que dado três vetores, não necessariamente num mesmo plano, pode ser que nenhuma combinação linear entre eles seja possível. Neste caso, estes vetores são denominados de linearmente independentes. Os três versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$, mostrados na Figura 1, são linearmente independentes.

Figura 1.	Figura 2.

Exercício 1. Desenhe os vetores posição $\vec{R}_{1}=(1,2,0)$ e $\vec{R}_{2}=(1,1,0)$ em um mesmo sistema cartesiano de coordenadas (ortonormal). Determine as coordenadas da soma $\vec{R}_{1}+\vec{R}_{2}$ e da diferença $\vec{R}_{1}-\vec{R}_{2}$ e represente-os no mesmo sistema de coordenadas anterior. Use o teorema de Pitágoras para determinar o comprimento de cada vetor.

Exercício 2. Primeiro note que as componentes dos versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ mostrados na Figura 1 são $\hat{\imath}=(1,0,0)$, $\hat{\jmath}=(0,1,0)$ e $\hat{k}=(0,0,1)$. Agora tente escrever, por exemplo, $\hat{k}=\alpha\hat{\imath}+\beta\hat{\jmath}$. Sabendo que a igualdade entre vetores somente é possível se houver uma igualdade entre suas componentes em cada direção, mostre que a combinação linear $\hat{k}=\alpha\hat{\imath}+\beta\hat{\jmath}$ resulta em três equações lineares. Mostre que duas destas equações lineares envolvem os escalares $\alpha$ e $\beta$, cuja soluções são $\alpha=0$ e $\beta=0$. Verifique que a terceira equação é inconsistente ($0=1$). Isto mostra que os versores $\hat{\imath}$, $\hat{\jmath}$ e $\hat{k}$ são linearmente independentes, isto é, não admitem uma combinação linear entre eles.