Cinemática
Cinemática: elementos geométricos e analíticos necessários à descrição do movimento, sem se preocupar com suas causas. Curvas espaciais descreverão trajetórias. Trajetórias serão descritas em sistemas de coordenadas. Movimento será descrito pelos vetores posição,
velocidade e aceleração. Taxas de variação serão descritas por derivadas. Espaço percorrido será descrito por integrais.
2. Geometria
2.2. Referencial
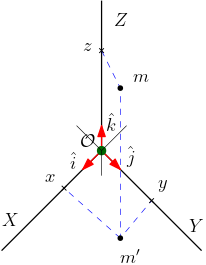
Muito bem, tendo estabelecido as principais propriedades do espaço euclidiano, precisamos construir um referencial para localizar pontos e curvas (restringindo aos objetos geométricos que nos interessa mais). Uma vez que estaremos considerando o espaço euclidiano tridimensional, o referencial mais simples deverá apresentar um ponto fixo (a origem) pelo qual passam três retas mutuamente ortogonais e indicar um sentido positivo em cada uma delas (eixos orientados). Denominemos de \(\mathcal{O}\) a origem, de $X$, $Y$ e $Z$ os eixos mutuamente perpendiculares e de $\hat{i}$, $\hat{j}$ e $\hat{k}$ os segmentos orientados de comprimentos unitários em cada eixo. Esses segmentos orientados unitários são denominados de versores. Um ponto $m$ será "localizado" neste referencial pelo seguinte procedimento geométrico:
- trace uma reta paralela ao eixo $Z$, passando por $m$, até interceptar o plano $XY$ em $m'$;
- trace uma reta paralela ao eixo $Y$, passando por $m'$, até interceptar o eixo $X$ em $x$;
- trace uma reta paralela ao eixo $X$, passando por $m'$, até interceptar o eixo $Y$ em $y$;
- trace uma reta paralela ao plano $XY$, passando por $m$, até interceptar o eixo $Z$ em $z$;
- as projeções $(x,y,z)$ são as coordenadas do ponto $m$.
A Figura 1 ilustra o ponto $m$, com coordenadas $m=(x,y,z)$, representado em um referencial com eixos $X$, $Y$ e $Z$ mutuamente perpendiculares (ortogonais), conhecido como sistema de coordenadas cartesiano, ou simplesmente sistema ortonormal de coordenadas, introduzido por René Descartes no Séc. XVII. Em geral usamos a origem para nomear um sistema de coordenadas. Neste caso, dizemos "o referencial (ortonormal) $\mathcal{O}$".
E se os eixos do referencial não forem ortogonais (perpendiculares)? Neste caso há mais de uma forma "canônica" de construirmos as coordenadas de um ponto. Você questionou o uso de retas paralelas (aos eixos) no procedimento geométrico usado para construir as coordenadas no referencial ortonormal? Por que não retas com uma outra inclinação? Para reduzir ao mínimo o número de possibilidades, o bom senso pede para usarmos retas paralelas ou perpendiculares aos eixos. A Figura 2 ilustra o uso de retas paralelas e perpendiculares aos eixos, resultando em projeções diferentes $(x,y)$ e $(\bar{x},\bar{y})$. Embora estas projeções distintas possam ser relacionadas, deixaremos este exercício para outra oportunidade.
Como podemos calcular a distância entre dois pontos usando suas coordenadas? A distância entre dois pontos é o comprimento do segmento de reta que os une. Por exemplo, o segmento de reta que une a origem $\mathcal{O}=(0,0,0)$ e o ponto $m=(x,y,z)$ na Figura 3 tem um comprimento igual a $\sqrt{x^{2}+y^{2}+z^{2}}$. Este resultado pode ser obtido aplicando o teorema de Pitágoras duas vezes (faça o Exercício 1). Este exemplo nos ensina que em geral a distância $d(A,B)$ entre dois pontos quaisquer $A=(x_{a},y_{a},z_{a})$ e $B=(x_{b},y_{b},z_{b})$ é
\begin{equation} d(A,B) =\sqrt{(x_{b}-x_{a})^{2}+(y_{b}-y_{a})^{2}+(z_{b}-z_{a})^{2}}. \end{equation}Esse resultado será válido mesmo se esses dois pontos estiverem infinitesimalmente próximos. Há outra utilidade para esta distância entre dois pontos num espaço euclidiano. Denominemos por vetor um segmento de reta com uma orientação (segmento orientado, flecha). Como todo segmento orientado inicia em um ponto, digamos $A=(x_{a},y_{a},z_{a})$, e termina em outro, digamos $B=(x_{b},y_{b},z_{b})$, então o comprimento (ou norma) $||\vec{AB}||$ do vetor $\vec{AB}$ é
\begin{equation} ||\vec{AB}|| =\sqrt{(x_{b}-x_{a})^{2}+(y_{b}-y_{a})^{2}+(z_{b}-z_{a})^{2}}. \end{equation}| Figura 1 |
Figura 2 |
Figura 3 |
|---|---|---|
 |
 |
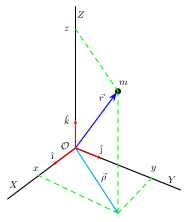 |
Exercício 1. Use o teorema de Pitágoras para determinar o comprimento do vetor $\vec{\rho}$ no plano $XY$ na Figura 3 em termos das coordenadas $x$ e $y$. Use régua e papel e lápis e
desenhe um triângulo retângulo formado com os catetos $x=4$ cm e $y=3$ cm. Verifique (experimentalmente) com sua régua que o comprimento da hipotenusa é muito próximo do valor calculado pelo teorema de Pitágoras.
Exercício 2. Use o resultado do exercício anterior e novamente o teorema de Pitágoras para determinar o comprimento do vetor $\vec{r}$ na Figura 3. Calcule o valor deste comprimento quando $x=4$ cm, $y=3$ cm e $z=5$ cm.
Exercício 3. Mostre que o comprimento do vetor $\vec{r}$ calculado no exercício anterior também pode ser obtido pela expressão $d(A,B)$ com o ponto $A$ sendo a origem $\mathcal{O}$ e o ponto $B$ sendo o ponto $m$ (veja a Figura 3).