Dinâmica
2. Segunda lei
2.5. Lançamento oblíquo
No lançamento oblíquo, um objeto de massa \(m\), sob ação da gravidade $\vec{F}_{g}$, dirigida ao solo, é lançado com uma determinada velocidade inicial $\vec{v}_{0}$. O experimento mostra uma trajetória plana com curvatura. Sendo plana, podemos colocá-la
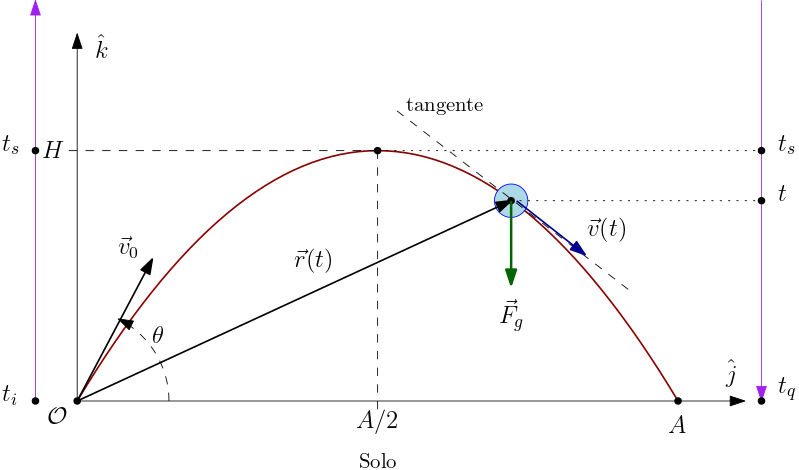
no plano YZ, por conveniência, com o eixo Z perpendicular ao solo (plano XY). Essa é a melhor escolha para o sistema de coordenadas nesse caso, a qual está ilustrada na Figura 1.
A Figura 1 exibe o vetor velocidade inicial $\vec{v}_{0}=\vec{v}(t_{i})$, o qual faz um ângulo $\theta$ ($0\leq\theta\leq\pi$) com o eixo Y (no solo). Por conveniência, escolheremos o instante inicial como sendo zero, $t_{i}=0$. Também por conveniência, escolheremos a origem como a posição inicial, $\vec{r}(t_{i})=0$. A Figura 1 exibe também o vetor posição $\vec{r}(t)$ no instante $t>t_{i}$, bem como o vetor velocidade neste mesmo instante. Lembre-se que a velocidade é sempre tangente à trajetória (mesmo que a curva representando a trajetória ainda não seja conhecida).
Escreva todos os vetores em coordenadas. Usando o sistema de coordenadas mostrado na Figura 1, temos a gravidade \begin{equation} \vec{F}_{g}=-mg\,\hat{k},\; g=9,8~\text{m}/\text{s}^{2}, \end{equation} o vetor posição \begin{equation} \vec{r}(t)=x(t)\hat{i}+y(t)\hat{j}+z(t)\hat{k},
\end{equation} o vetor velocidade \begin{equation} \vec{v}(t)=\dot{x}(t)\hat{i}+\dot{y}(t)\hat{j}+\dot{z}(t)\hat{k}, \end{equation} e o vetor aceleração \begin{equation} \vec{a}(t)=\ddot{x}(t)\hat{i}+\ddot{y}(t)\hat{j}+\ddot{z}(t)\hat{k}. \end{equation}
Finalmente, as condições iniciais, \begin{equation} x(0)=y(0)=z(0)=0 \end{equation} e \begin{equation} \dot{x}(0)=0, \dot{y}(0)=v_{0}\cos\theta, \dot{z}(0)=v_{0}\sin\theta. \end{equation}
Momento de usar a segunda lei $\vec{F}_{g}=m\vec{a}$ (massa constante) na forma de coordenadas, \begin{equation} -mg\,\hat{k}= m\ddot{x}(t)\hat{i}+ m\ddot{y}(t)\hat{j}+ m\ddot{z}(t)\hat{k}, \end{equation} a qual implica em três EDOs (a igualdade vetorial
implica na igualdade entre coordenadas em cada eixo; verifique), \begin{equation} 0=\ddot{x}(t),\; 0=\ddot{y}(t),\; -g=\ddot{z}(t). \end{equation} Essas EDOs são, essencialmente, do mesmo tipo: derivada segunda igual a uma constante. De acordo com a Seção Introito, cada equação horária será um polinômio no tempo $t$ (verifique), \begin{align} x(t) &= c_{1}+c_{2}t,\\ y(t) &= c_{3}+c_{4}t,\\ z(t) &= c_{5}+c_{6}t-\frac{1}{2}gt^{2}. \end{align} As seis coordenadas serão
determinadas pelas condições iniciais (verifique), \begin{equation} c_{1}=c_{3}=c_{5}=0, \end{equation} e \begin{equation} c_{2}=0, c_{4}=v_{0}\cos\theta, c_{6}=v_{0}\sin\theta. \end{equation}
Desta forma, esta trajetória é representada pela curva cuja forma
paramétrica é dada pelas equações horárias
\begin{align}
x(t) &= 0,\\
y(t) &= v_{0}\cos\theta\, t,\\
z(t) &= v_{0}\sin\theta\, t-\frac{1}{2}gt^{2}.
\end{align}
Esta curva é uma parábola no plano YZ. Consequentemente, as
componentes do vetor velocidade são,
\begin{align}
v_x(t) &= 0,\\
v_y(t) &= v_{0}\cos\theta,\\
v_z(t) &= v_{0}\sin\theta-gt.
\end{align}
O módulo desse vetor velocidade, necessário para calcular o
comprimento da trajetória, é (verifique)
\begin{equation}
v^{2}(t)=\vec{v}\cdot\vec{v}= v_{0}^{2}-2v_{0}\sin\theta\, gt +(gt)^2.
\end{equation}
Como o comprimento da trajetória é a integral do módulo do vetor
velocidade
\begin{equation}
\Delta s=\int\limits_{t=0}^{t=t_{q}}\! v(t)\, dt=f(\theta),
\end{equation}
ele se torna uma função do ângulo $\theta$ de lançamento. Assim, o
maior comprimento ocorre para um ângulo $\theta_{m}$ quando esta
função $f(\theta)$ passa pelo seu máximo (um dos extremos),
satisfazendo (verifique)
\begin{equation}
\left.\frac{df}{d\theta}\right|_{\theta=\theta_{m}}=0 \implies
\theta_{m}=\frac{\pi}{2}.
\end{equation}
Esse também é o ângulo para o qual o alcance é máximo (verifique).
Dica: use o fato da derivada de uma função composta (como a raiz quadrada) ser proporcional à derivada de seu argumento.
Modelagem. Apenas observando o experimento é impossível afirmar que a trajetória de um objeto lançado obliquamente é uma parábola. Mais difícil ainda identificar o ângulo para o qual o alcance (e o comprimento da trajetória) é máximo. Quando o sistema mecânico é simulado por um modelo matemático, previsões podem ser feitas sem a necessidade de experimentos. Como a força resultante é paralela ao eixo vertical, o eixo Z, a segunda lei nos diz que o momentum linear é conservado nas demais direções (onde as componentes da força resultante são nulas). A conservação do momentum linear no eixo X é trivial, pois não há movimento lá. No entanto, a conservação do momentum linear no eixo Y, mais uma previsão do modelo matemático, somente pode ser observada após uma série de medidas cuidadosas da velocidade neste eixo. Outro resultado que jamais poderia ser percebido somente pela experimentação: a trajetória não depende da massa do objeto. Isto significa que as trajetórias de uma bola de gude e de um fusca serão idênticas quando lançados sob as mesmas condições iniciais. Este modelo (ainda) não leva em consideração a presença da atmosfera (se houver).
Exercícios. Detalhe todas as passagens sinalizadas por "verifique''.