Dinâmica
| Site: | Moodle USP: e-Disciplinas |
| Curso: | Física Básica I |
| Livro: | Dinâmica |
| Impresso por: | Usuário visitante |
| Data: | quarta-feira, 3 jul. 2024, 10:16 |
1. Leis de Newton
As leis de Newton são apresentadas sob a forma de princípios derivados de um experimento simples envolvendo colisões entre objetos. Surpreendente que o movimento de objeto obedeçam leis passíveis de uma descrição matemática simples, elegante e eficiente.
1.1. Introdução
Que é uma lei (ou princípio)? No que diz respeito às leis da natureza, o dicionário nos diz que uma lei (da natureza) é "aquilo que se impõe ao homem por sua razão, consciência ou por determinadas condições ou circunstâncias". Em outras palavras, uma lei física é uma afirmação fundamental, passível de verificação, formando a base de uma teoria. Portanto, uma teoria é um conjunto de leis.
É importante fazermos um paralelo entre Física e Matemática. Em Matemática, o postulado é o equivalente de uma lei em Física, porém com uma diferença muito importante: um postulado nem sempre está sujeito à verificação. Por estarem sempre sujeitas a verificações, as leis físicas estão sempre em estado de alerta.
A história tem nos mostrado que uma lei física não é imutável. Basta uma única experiência bem sucedida que mostre claramente a violação de uma determinada lei para que ela seja abandonada ou corrigida. Por exemplo, até a década de 60, acreditava-se que um processo físico e a sua imagem (como num espelho) fossem idênticos, isto é, produzissem os mesmos resultados. Esta lei ficou conhecida como a lei da conservação da paridade (sem distinção entre direito e esquerdo; similaridade). Todavia, dois jovens físicos, C. N. Yang e T. D. Lee, fizeram em 1956 uma previsão (ou observação) onde esta lei da conservação da paridade pudesse ser violada em processos de desintegração nuclear (decaimento beta). Esta previsão foi confirmada em 1957 em um belíssimo experimento conduzido por Madame Wu (C. S. Wu). Neste caso, a conservação da paridade foi descartada como uma lei.
Um outro exemplo: a teoria Newtoniana da gravitação é capaz de explicar razoavelmente bem, o comportamento mecânico do nosso sistema solar, ou seja, reproduz as leis de Kepler. Todavia, existem alguns efeitos minuciosos que a teoria Newtoniana da gravitação não consegue explicar (reproduzir). Dois deles, o desvio da luz ao passar próxima de um corpo estelar como o nosso sol e a precessão do periélio do planeta Mercúrio, quando calculados com a teoria Newtoniana não concordam plenamente com as observações. A reconciliação entre teoria e experimento só é possível no contexto da Relatividade Geral de Einstein (1915). Neste caso, a teoria Newtoniana foi corrigida pela Relatividade Geral. A relatividade geral nos revelou que a matéria (e/ou energia) diz ao espaço-tempo como se deformar (curvar e torcer) e, por sua vez, o espaço deformado dita à matéria como ela deve se mover. Mesmo as leis de Newton para o movimento translacional que estamos prestes a discutir valem somente para velocidades baixas em comparação com a velocidade da luz. Para velocidades comparáveis à da luz, a Mecânica Newtoniana é corrigida pela Mecânica Relativística (Einstein, 1905), como veremos mais tarde. Além de corrigir a Mecânica Newtoniana, a Relatividade Especial de Einstein nos revelou a fusão entre espaço e tempo (o tempo não é absoluto como na Mecânica Newtoniana) bem como entre energia e massa (\(\Delta E=\Delta m\,c^{2}\)).
Restrições. Sabemos construir a trajetória de um ponto material usando curvas espaciais em um espaço Euclidiano tridimensional. Também sabemos determinar velocidade e aceleração, bem como o espaço percorrido, em qualquer instante de tempo. Portanto, é hora de passarmos ao estudo das leis físicas que determinam e controlam o movimento de corpos macroscópicos (que não sejam muito mais massivos que o Sol) com velocidades muito inferiores à velocidade da luz no vácuo (aproximadamente 300000 km/s). Estas leis são conhecidas por "leis de Newton" do movimento. As duas restrições mencionadas (corpos macroscópicos de baixa massa e com baixas velocidades) são importantes, pois as leis Newtonianas deixam de ser válidas em três ocasiões: (1) no mundo microscópico de dimensões atômicas (neste caso as leis Newtonianas são corrigidas pelas leis da Física Quântica), (2) quando as velocidades envolvidas são comparáveis à velocidade da luz no vácuo (neste caso as leis Newtonianas são corrigidas pelas leis da Relatividade Especial de Einstein) e (3) para corpos extremamente massivos , como estrelas de nêutrons (neste caso as leis Newtonianas são corrigidas pela Relatividade Geral de Einstein).
1.2. Experimento
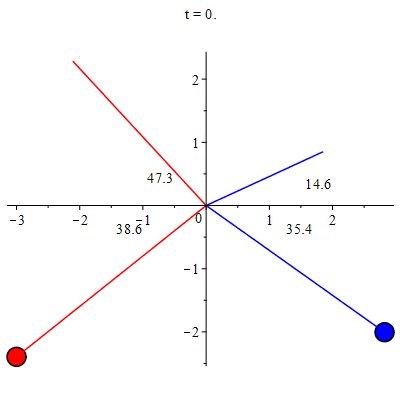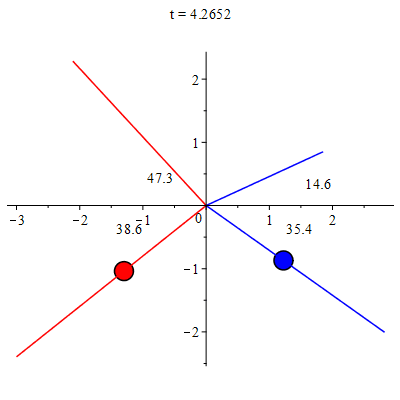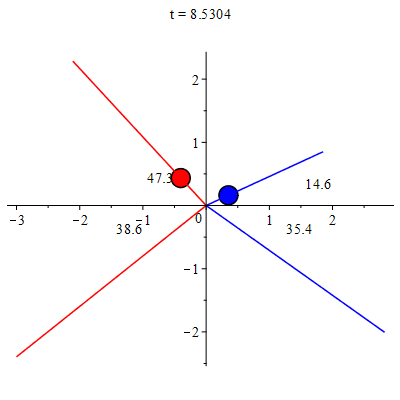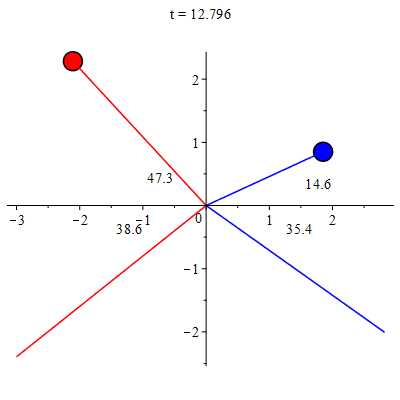
Imagine três objetos completamente isolados e que podem movimentar-se livremente num plano. Cuidadosamente, observa-se a colisão entre os três pares possíveis. Seja \(\vec{v}_{i}\) as velocidades de cada objeto ($i\in\{1,2,3\}$) antes da colisão e $\vec{u}_{i}$
as velocidades após a colisão. Como estes objetos estão isolados e interagem somente no momento da colisão, os vetores velocidades mudam apenas durante a colisão. A direção e a rapidez (módulo) de cada vetor velocidade são anotadas e analisadas cuidadosamente.
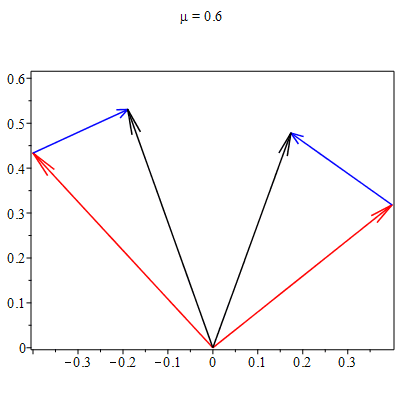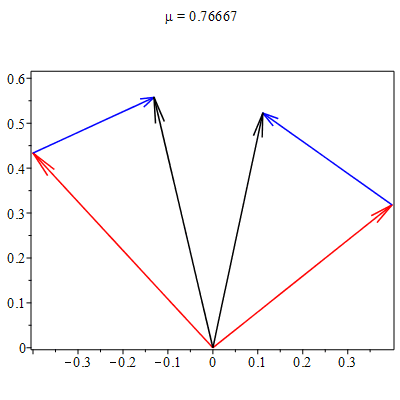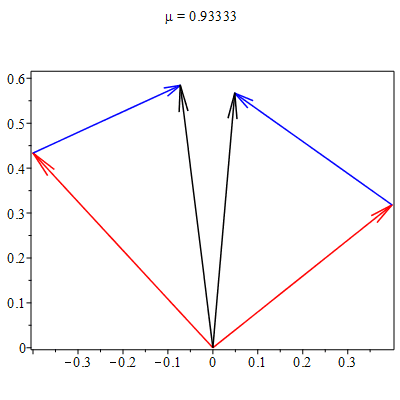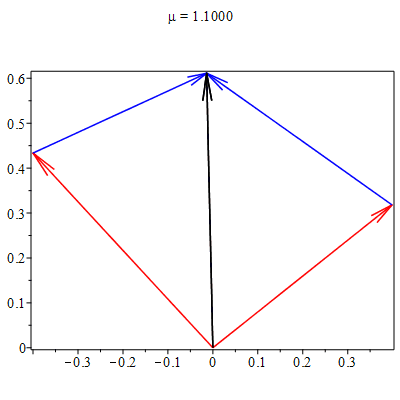
A Figura 1 ilustra uma destas colisões (lado esquerdo).
Após uma análise meticulosa, verifica-se que há uma combinação linear entre os vetores velocidades, particular de cada experimento, que se mantém a mesma antes e depois da colisão, \begin{equation} \vec{v}_{i}(t) + \mu_{ij}\vec{v}_{j}(t) = \vec{u}_{i}(t) + \mu_{ij}\vec{u}_{j}(t), \end{equation} onde $\mu_{ij}$ são números reais e positivos. Para cada colisão existe um único valor de $\mu_{ij}$ que torna verdadeira a igualdade acima, como mostrado no lado direito da Figura 1. Outro resultado surpreendente: os valores dos parâmetros $\mu_{ij}$,
determinados em cada experimento, satisfazem \begin{equation}
\mu_{12}\mu_{23}\mu_{31}=1. \end{equation} Como veremos a seguir, a análise deste experimento nos permite extrair dois princípios equivalentes às três leis de Newton, bem como o conceito operacional de massa (inercial).
1.3. Os princípios
- Princípio 1
- Existem certos referenciais, denominados de inerciais (no sentido de incapacitados), com as seguintes propriedades.
- Cada corpo isolado move-se em uma linha reta neste referencial inercial.
- A noção de tempo pode ser quantificada: uma unidade de tempo pode ser definida através do movimento uniforme de um corpo isolado neste referencial inercial.
- Cada corpo isolado move-se com uma velocidade constante neste referencial inercial.
- Cada corpo isolado move-se em uma linha reta neste referencial inercial.
Estas três propriedades definem um referencial inercial. Note que um corpo isolado não tem aceleração em um referencial inercial. Assim, podemos
definir, pelo menos operacionalmente, tempo como sendo um parâmetro \(t\) proporcional ao comprimento $s$ da trajetória de um corpo isolado (velocidade constante) em um referencial inercial: \begin{equation}\Delta
s(t)=\int_{0}^{\Delta t}v\,dt = v\,\Delta t\implies \Delta t=\frac{\Delta s}{v}.\end{equation} Naturalmente, qualquer outro parâmetro $t'$ definido como tempo, usando um outro corpo isolado, estará relacionado de forma linear com o primeiro parâmetro
$t$, pois os comprimentos de duas trajetórias quaisquer são sempre proporcionais. Note também que podemos medir apenas intervalos de tempo, proporcionais ao comprimento da trajetória, e nunca os valores absolutos do "tempo".
Como vimos anteriormente, o comprimento de uma trajetória é calculado através de uma integral. Assim, usar o comprimento de uma trajetória para medir intervalos de tempo não é prático. Desde há muito tempo, temos usado o movimento de rotação da Terra
em torno de seu próprio eixo, praticamente constante, como um instrumento (relógio) para medir intervalos de tempo. Qualquer processo repetitivo, com uma frequência praticamente constante, pode
ser usado como um relógio. Os relógios mais precisos que dispomos no momento são os chamados "relógios atômicos", baseados na impressionante regularidade de certos processos nucleares (portanto, pertencentes ao domínio da Física Quântica). Em um relógio
atômico, o erro é de apenas um segundo em um milhão de anos. Um fato importante: embora não sabemos exatamente o que é o tempo, sabemos operar com ele, isto é, sabemos medir intervalos de tempo. Em geral, escolhemos um intervalo padrão como unidade
de tempo e todos os demais intervalos são medidos por comparação.
- Princípio 2
- Considere três corpos isolados sendo observados em um referencial inercial. Estes corpos podem interagir apenas entre si, sempre aos pares. Sejam $\vec{v}_{i}(t)$, $i\in\{1,2,3\}$, seus vetores velocidades e $t$ o tempo. Então as duas propriedades seguintes
se verificam.
- Existem experimentos envolvendo a colisão entre dois corpos cujos resultados podem ser expressados como \begin{equation}\vec{v}_{i}(t) + \mu_{ij}\vec{v}_{j}(t) = \vec{P}_{ij},\end{equation} onde os escalares $\mu_{ij}$ e os vetores $\vec{P}_{ij}$
são constantes, isto é, são independentes do tempo. As constantes vetoriais $\vec{P}_{ij}$ dependem do experimento, do referencial inercial e dos dois corpos envolvidos.
- As constantes escalares $\mu_{ij}$ são positivas e não dependem do experimento e nem do referencial inercial. Elas dependem apenas dos dois corpos envolvidos e satisfazem \begin{equation}\mu_{12}\mu_{23}\mu_{31}=1.\end{equation}
- Existem experimentos envolvendo a colisão entre dois corpos cujos resultados podem ser expressados como \begin{equation}\vec{v}_{i}(t) + \mu_{ij}\vec{v}_{j}(t) = \vec{P}_{ij},\end{equation} onde os escalares $\mu_{ij}$ e os vetores $\vec{P}_{ij}$
são constantes, isto é, são independentes do tempo. As constantes vetoriais $\vec{P}_{ij}$ dependem do experimento, do referencial inercial e dos dois corpos envolvidos.
Algumas observações são necessárias. Observe que devido ao fato das constantes $\mu_{ij}>0$ obedecerem à condição acima, elas podem ser escritas numa forma racional $\mu_{ij}=m_{j}/m_{i}$, com $m_{i}>0$ (isso é um teorema). Em termos destas novas
constantes, os resultados anteriores podem ser re-escritos como \begin{equation}m_{i}\vec{v}_{i}(t) + m_{j}\vec{v}_{j}(t) = \vec{p}_{ij},\quad \vec{p}_{ij}=m_{i}\vec{P}_{ij}. \end{equation} A quantidade vetorial definida por \begin{equation} m_{i}\vec{v}_{i}(t)\equiv
\vec{p}_{i}(t) \end{equation} é denominada de momentum linear (ou quantidade de movimento) do $i$-ésimo corpo. A constante vetorial $\vec{p}_{ij} = \vec{p}_{i}(t)+\vec{p}_{j}(t)$ é o momentum linear
total dos dois corpos envolvidos em cada experimento e é uma constante quando estes dois corpos estão isolados. A constante $m_{i}>0$ é denominada de carga inercial (ou massa inercial, ou simplesmente
massa, por razões históricas). Note que apenas a razão $\mu_{ij}$ é determinada pelo experimento. Portanto, podemos determinar apenas as razões $\mu_{ij}=m_{j}/m_{i}$ entre massas. Isto significa que temos de eleger um corpo padrão, cuja massa
deve ser assumida como uma unidade de massa, digamos $m_{i}=1$ Kg. Então a massa $m_{j}=\mu_{ij}$ é determinada univocamente do experimento. Novamente, mesmo não sabendo o que é massa, somos capazes de operar com ela, escolhendo um padrão e realizando
comparações.
1.4. As leis de Newton
E as famosas três leis de Newton para o movimento? Onde estão? Elas estão contidas nos dois princípios apresentados. A primeira lei de Newton, ou lei da inércia, está contida no Princípio 1.
Uma partícula isolada em um referencial inercial ou está em repouso ou está em movimento uniforme. Note que não estamos usando o conceito de forças no Princípio 1. Não devemos esquecer que o Princípio 1 também nos dá uma definição operacional
de tempo.
A segunda lei de Newton está contida no Princípio 2, \( \) \begin{equation}\vec{F}_{R}=\frac{d}{dt}\vec{p},\quad \vec{p}=m\vec{v},\end{equation} onde $\dot{\vec{p}}=m\vec{a}$ para
massas constantes. Em geral, a força resultante $\vec{F}_{R}$ é conhecida independentemente do momentum linear, ou seja, a segunda lei de Newton não é uma mera definição de força e nem de massa. Ela representa um fato experimental: uma força muda o
estado de movimento de uma massa $m$ de acordo com a segunda lei.
De fato, como nestes experimentos de colisão o momentum linear total $\vec{p}_{ij} = \vec{p}_{i}(t)+\vec{p}_{j}(t)$ é constante, então, derivando no tempo os dois lados desta expressão, assumindo que as massas $m_{i}$ sejam constantes, temos \begin{equation}
m_{i}\vec{a}_{i}(t) + m_{j}\vec{a}_{j}(t) = 0.\quad (\ast) \end{equation} O que esta expressão nos revela. Apesar dos dois corpos estarem isolados, eles interagem entre si no momento da colisão. Esta interação produz mudanças nas velocidades (ou na quantidade de
movimento) acarretando nesta relação. Naturalmente, as acelerações são diferentes de zero apenas durante o (curto) intervalo de tempo da colisão. Como temos apenas dois corpos, isto significa que cada parcela na relação acima deve ser idêntica
à interação sofrida por um dos corpos no momento da colisão. Esta interação entre estes dois corpos, capaz de mudar o vetor velocidade, denominaremos de força. Força é um vetor. Assim, podemos
concluir que uma força $\vec{F}_{i}(t)$ agindo num objeto de massa $m_{i}$ (constante) altera seu movimento de acordo com \begin{equation}\vec{F}_{i}(t) = m_{i}\vec{a}_{i}(t) = \frac{d}{dt}\vec{p}_{i}.\end{equation} No nosso experimento,
esta é a forma com que a força devida ao $j$-ésimo objeto atua sobre o $i$-ésimo objeto durante a colisão. Aprendemos com estes experimentos que é necessário um agente físico (força) para alterar o estado de movimento de um corpo material e que esta
força é a taxa de variação do momentum linear (segunda lei de Newton). Ao contrário do momentum linear, definido por $\vec{p}=m\vec{v}$, a segunda lei $\vec{F}=\dot{\vec{p}}$, ou $\vec{F}=m\vec{a}$ para massa constante, não é uma definição de força
e nem de massa. A segunda lei de Newton é o resultado de uma observação experimental.
Desta forma, o resultado experimental $(\ast)$ pode ser re-escrito como \begin{equation}\vec{F}_{R}=\vec{F}_{ij}(t) + \vec{F}_{ji}(t) = 0.\quad (\ast\ast) \end{equation} Note que $\vec{F}_{ij}(t)=m_{i}\vec{a}_{i}(t)$ é a força que o corpo $j$ faz no corpo $i$ e $\vec{F}_{ji}(t)=m_{j}\vec{a}_{j}(t)$ é a força que o corpo $i$ faz no corpo $j$, portanto elas atuam em corpos diferentes. Ainda mais, a soma vetorial nula em $(\ast\ast)$ implica em $|\vec{F}_{ij}|=|\vec{F}_{ji}|$ e $\vec{F}_{ij}\,//-\vec{F}_{ji}$ (vetores anti-paralelos). Consequentemente, $(\ast\ast)$ expressa a terceira lei de Newton (ação e reação). Portanto, a terceira lei de Newton também está contida no Princípio 2.
1.5. Leis de conservação
Dada e relação entre o momentum linear e força na segunda lei \( \) \begin{equation} \vec{F}=\dot{\vec{p}},\quad \vec{p}=m\vec{v},\end{equation} se a força (ou uma de suas componentes) é nula, então o momentum linear (ou a respectiva componentes) é constante. Uma quantidade constante no tempo é denominada de
quantidade conservada. Então temos o teorema da conservação do momentum linear,
- Teorema 1
- Se a força resultante em um sistema físico é nula em um referencial inercial, então o momentum linear total deste sistema é conservado (não varia no tempo).
A utilidade de uma quantidade conservada reside no fato dela possuir os mesmos valores em tempos diferentes. Por exemplo, a quantidade de movimento total $\vec{p}_{ij}(t)$ é conservada no nosso experimento de colisões. Então, se denotarmos por $t_{1}$ um tempo antes da colisão e por $t_{2}$ um tempo depois da colisão, teremos $\vec{p}_{ij}(t_{1})=\vec{p}_{ij}(t_{2})$, a qual pode ser usada para determinar alguma quantidade desconhecida contida nela, o valor da constante $\mu_{ij}$ neste caso. De fato, do experimento temos \begin{equation} \vec{v}_{i} + \mu_{ij}\vec{v}_{j} =
\vec{u}_{i} + \mu_{ij}\vec{u}_{j}, \end{equation} onde $\vec{v}_{i}$ são as velocidades de cada objeto ($i\in\{1,2,3\}$) antes da colisão e $\vec{u}_{i}$
são as velocidades após a colisão e os números $\mu_{ij}$ são determinados pelas componentes destes vetores velocidades. Para isolar os escalares $\mu_{ij}$, temos necessariamente de reescrever esta quantidade conservada em termos de suas componentes (subíndice $k\in\{1,2\}$), \begin{equation} \mu_{ij}=\frac{v_{i,k}-u_{i,k}}{u_{j,k}-v_{j,k}}. \end{equation} Note que estes valores são independentes das duas direções $k$ do plano contendo os vetores velocidades.
Naturalmente, o momentum linear tem um papel importante na Mecânica Newtoniana. Esta importância é devida à própria segunda lei e também ao Teorema 1 sobre a conservação do momentum linear. Portanto, podemos dizer que a sua definição como $\vec{p}=m\vec{v}$ está muito bem justificada pelo seu conteúdo físico.
1.6. Massa inercial
Qual é a importância da massa \(m\) que aparece na quantidade conservada \begin{equation}m_{i}\vec{v}_{i}(t) + m_{j}\vec{v}_{j}(t) = \vec{p}_{ij}? \end{equation} O experimento nos revelou que o momentum linear total $\vec{p}_{ij}$ do sistema (isolado) formado apenas pelos corpos $i$ e $j$ é constante. Se fizermos $m_{j}=0$, então resulta que $\vec{v}_{i}$ é também uma constante, ou seja, o corpo $i$ está em movimento uniforme. No entanto, se este mesmo corpo $i$ também tivesse uma massa nula, $m_{i}=0$, então a sua quantidade de movimento seria nula. Isto nos sugere que é necessário que um corpo tenha massa não-nula para poder ter uma quantidade de movimento não-nula. Desta forma, podemos afirmar que a condição de estar em movimento uniforme em um referencial inercial depende exclusivamente de ter uma massa não-nula.
Vale mencionar que até a época de Newton (até o Séc. 16, portanto um pouco mais de 2000 anos depois de Aristóteles) acreditava-se que era necessário uma força para manter um corpo em movimento, mesmo em movimento uniforme. Assim, a massa $m$ na segunda lei \begin{equation} \vec{F}=\dot{\vec{p}},\quad \vec{p}=m\vec{v},\end{equation} passou a ser conhecida também por massa inercial. Considerando massas constantes, $\vec{F}=m\vec{a}$. Vemos que aumentando a massa (através de uma troca de objetos), devemos aumentar também a intensidade da força para manter a intensidade da aceleração no mesmo valor. Isto significa que temos de esforçar mais para mudar o estado de movimento de um corpo com uma maior massa. Esta resistência em mudar o estado de movimento é quantificada pela massa inercial. Em outras palavras, a massa inercial mede a resistência de um corpo em mudar seu estado de movimento. A massa inercial é uma propriedade intrínseca de qualquer objeto.
2. Segunda lei
A segunda lei de Newton é um programa para criar a trajetória que um determinado objeto deve seguir sob a ação de uma determinada força. Força é uma função vetorial que modela a interação de um objeto com o seu meio.
2.1. Introdução
Em geral dada uma força resultante \(\vec{F}\) agindo em um objeto de massa inercial $m$, dadas a posição inicial $\vec{r}(t_{0})$ e a velocidade inicial $\vec{v}(t_{0})$, queremos determinar a posição $\vec{r}(t)$ desse objeto em qualquer instante de
tempo $t$ posterior ao instante inicial $t_{0}$. Determinar trajetórias criadas por forças resultantes é o objetivo básico da Mecânica. A implementação desse objetivo é feita pela segunda lei $\vec{F}=\dot{\vec{p}}$, com $\vec{p}=m\vec{v}$ (momentum
linear).
Para compreendermos como a segunda lei fornece trajetórias, vamos considerá-la com a massa inercial constante,\begin{equation}\vec{F}=\frac{d\vec{p}}{dt}=m\frac{d\vec{v}}{dt}.\end{equation} O lado direito da segunda lei é proporcional à aceleração, a
segunda taxa de variação do vetor posição, o qual representa a trajetória na forma paramétrica. O lado esquerdo da segunda lei é proporcional à força, uma expressão matemática da interação mantida pelo objeto de massa $m$. Em princípio, estes dois vetores,
força e aceleração, possuem naturezas completamente distintas. A igualdade entre eles na segunda lei somente é possível com a presença da massa inercial. Assim, as dimensões de força são \begin{equation} [\vec{F}]=\left[m\vec{a}\right]=\frac{ML}{T^{2}}.\end{equation}
Em geral, a força deve ser determinada experimentalmente, ou por conjecturas, e poderá depender da posição $\vec{r}$ e da velocidade $\dot{\vec{r}}$. Em algumas ocasiões raras, a força poderá depender da aceleração e do próprio tempo. Considerando $\vec{F}=\vec{F}(\vec{r},\dot{\vec{r}})$, a segunda lei assume a forma \begin{equation}\vec{F}\bigl(\vec{r},\frac{d\vec{r}}{dt}\bigr) = m\frac{d^{2}\vec{r}}{dt^{2}},\end{equation} ou, em coordenadas, \begin{equation} F_{i}\bigl(\vec{r},\frac{d\vec{r}}{dt}\bigr) = m\frac{d^{2}x_{i}}{dt^{2}},\; \vec{r}=(x_{1},x_{2},x_{3}).\end{equation} Portanto, do ponto de vista operacional, a segunda lei é um conjunto de três equações, tendo como incógnitas as componentes $x_{i}$ do vetor posição $\vec{r}$.
No entanto, estas não são equações convencionais, pois as incógnitas $x_{i}$ são funções do tempo $t$, $x_{i}=x_{i}(t)$. Além disso, aparecem nestas mesmas equações, as derivadas primeira e segunda destas mesmas incógnitas. Uma equação deste tipo recebe o nome de equação diferencial ordinária (ou simplesmente EDO). Um pouquinho sobre nomenclatura. As equações horárias $x_{i}=x_{i}(t)$ são as variáveis dependentes (as incógnitas). O tempo $t$ é a variável independente. Todas as derivadas numa equação diferencial ocorrem em termos das variáveis independentes. Quando temos apenas uma variável independente, como nesse caso, a equação diferencial é dita ser ordinária (EDO). Quando há mais de uma variável independente, a equação diferencial é dita ser parcial (EDP). A ordem de uma equação diferencial é dada pela ordem da derivada mais alta. Na segunda lei, a derivada mais alta é de ordem dois. Assim, nossas EDOs serão todas de segunda ordem.
- Teorema 2
- A solução $f=f(t,c_{1},c_{2})$ de uma EDO de segunda ordem contém duas constantes arbitrárias $c_{1}$ e $c_{2}$.
Esse Teorema 2 exige que disponibilizemos duas informações adicionais para que uma equação horária determinada pela segunda lei seja única. Estas informações adicionais serão dadas pela posição inicial $x_{i}(t_{0})$ e pela velocidade inicial $\dot{x}_{i}(t_{0})$, denominadas de condições iniciais. O instante inicial $t_{0}$ pode ser escolhido convenientemente.
Então estamos numa posição bastante confortável. Dado a força resultante $\vec{F}$ e as condições iniciais, $\vec{r}(t_{0})$ e $\vec{v}(t_{0})$, usamos as EDOs fornecidas pela segunda lei $\vec{F}=m\vec{a}$ para determinamos a trajetória $\vec{r}(t)$ e, consequentemente, o vetor velocidade $\vec{v}(t)$. O vetor aceleração já está dada pelo segunda lei $\vec{a}=\vec{F}/m$. Isto significa que podemos prever todo o comportamento do nosso sistema em qualquer instante de tempo $t\geq t_{0}$. Esse é o programa Newtoniano para determinar trajetórias. Desta forma, podemos afirmar que a Mecânica Newtoniana é completamente determinística. Preço: aprender a resolver EDOs!
2.2. Introito
Uma equação diferencial ordinária (EDO), como o primeiro nome diz, é uma equação. Esta equação relaciona termos conhecidos e desconhecidos compostos por funções e suas derivadas. A brincadeira consiste em determinar as funções mais gerais que respeitem
as equações nas EDOs. Caso ainda não teve contato com equações diferenciais ordinárias (EDOs) mas teve contato com derivadas e integrais, então já fez uso de EDOs mesmo não sabendo que estava fazendo.
Exemplo 1. Suponha \(x(t)\) uma função (desconhecida) do tempo $t$ satisfazendo a seguinte EDO de primeira ordem: \begin{equation}\dot{x}=\frac{dx}{dt}=\alpha,\end{equation} onde $\alpha$ é um parâmetro (constante) real. Pergunta: quem é a função $x$ de $t$ que derivada uma vez resulta numa constante? Essa pergunta é a verbalização da EDO dada. Esta EDO é tão simples que a função procurada, $x(t)$, pode ser encontrada usando o teorema fundamental do cálculo, \begin{equation} x(t)=\alpha t+\beta,\end{equation} onde $\beta$ é outra constante. A verificação é imediata: basta tomar a derivada primeira. O resultado já é a própria EDO dada. Note que fizemos uso apenas do teorema fundamental do cálculo. Nós adivinhamos a solução usando apenas nossos conhecimentos de derivadas e integrais das funções elementares. É uma adivinhação educada.
Exemplo 2. Suponha $x(t)$ uma função (desconhecida) do tempo $t$ satisfazendo a seguinte EDO de segunda ordem: \begin{equation} \ddot{x}=\alpha,\end{equation} onde $\alpha$ é um parâmetro (constante)
real. Pergunta: quem é a função $x$ de $t$ que derivada duas vezes resulta numa constante? Novamente, usando nossos conhecimentos de derivadas e integrais das funções elementares, a solução deve ser um polinômio quadrático, \begin{equation} x(t)=\frac{\alpha}{2}
t^{2}+\beta t+\gamma,\end{equation} onde $\beta$ e $\gamma$ são constantes. A verificação é imediata: \begin{equation} \dot{x}=\alpha t+\beta,\; \ddot{x}=\alpha.\end{equation}
A propósito, o Teorema Fundamental do Cálculo:
- Teorema 3
- Seja $f(t)$ uma função contínua e $F(t)$ a sua integral (indefinida), \begin{equation}\int f(t)\, dt = F(t).\end{equation} Então, \begin{equation}\frac{d}{dt}F(t) = f(t).\end{equation}
Sob a luz deste teorema, a EDO de primeira ordem no Exemplo 1 pode resolvida formalmente. Basta integrar no tempo os dois lados desta EDO, \begin{equation} \int \dot{x}\, dt= \int\alpha\, dt\implies x(t)=\alpha t+\beta,\end{equation} e usar o Teorema
Fundamental do Cálculo no lado esquerdo e resolver a integral do lado direito. Note que precisamos conhecer o integrando para resolver a integral do lado direito. Esta é uma técnica conhecida por separação de variáveis,
onde há uma separação completa entre as variáveis dependentes e independentes. Aplicando esta técnica duas vezes, resolvemos a EDO de segunda ordem no Exemplo 2 (verifique).
Todo processo dinâmico, em todas as áreas do conhecimento, é controlado por equações diferenciais. O estudo de equações diferenciais é uma das áreas mais importantes do conhecimento científico. Aprenda o que puder sobre equações diferenciais.
2.3. Gravidade
A gravidade é a força que a Terra exerce sobre qualquer objeto nas proximidades de sua superfície. Newton (Séc. XVII) foi o primeiro a propor um modelo matemático para
a gravidade, principalmente baseado nos trabalhos de outros cientistas-filósofos como Galileu e Kepler (ambos do Séc. XVI). A gravidade Newtoniana estabelece que um objeto de massa (inercial) \(m\) acima da superfície terrestre fique sujeito a uma força
da forma \begin{equation} \vec{F}_{g}=-mg\,\hat{r},\; g=9,8\,\text{m}/\text{s}^{2},\end{equation} onde o versor $\hat{r}$ está orientado do centro da Terra para a sua superfície (em relação ao nível do mar). Portanto, a força da gravidade é atrativa e
radial. Pela intensidade dela ser a mesma numa superfície esférica concêntrica com o centro da Terra, a gravidade é uma força com simetria esférica. A constante $g$ foi medida por Galileu, um século antes de Newton. Na verdade $g$ varia com a distância
ao centro da Terra, mas é praticamente constante para alturas em torno de alguns quilômetros acima da superfície média da Terra. Em São Carlos, SP, $g\approx 9,9\,\text{m}/\text{s}^{2}$.
A presença da massa inercial na expressão da força da gravidade Newtoniana é uma novela interessante per si. Newton imaginou que objetos tinham algum tipo de carga gravitacional que permitia a interação atrativa com a Terra. Newton denotou esta carga gravitacional por $m_{g}$. Esta ideia é baseada na existência de cargas elétricas como responsáveis pela força Coulombiana (de atração ou repulsão). Então, visto que existe uma atração de objetos pela Terra, é imediato supor a existência de um novo tipo de carga responsável por esta atração gravitacional: a carga gravitacional. Segundo o próprio Newton, esta força gravitacional tinha que ser da forma \begin{equation} \vec{F}_{g}=-m_{g}g\,\hat{r}.\end{equation} Esta era a forma que reproduzia os resultados de Kepler (as leis de Kepler para o movimento dos planetas no sistema solar). Newton já havia estabelecido sua segunda lei. Portanto, de acordo com a segunda lei, \begin{equation} \vec{F}_{g}=-m_{g}g\,\hat{r}=m_{i}\vec{a},
\end{equation} onde $m_{i}$ é a massa inercial. Ao medir o módulo $a$ da aceleração de um objeto em queda livre, Galileu identificou um resultado surpreendente: $a\approx g$. Newton realizou uma série de experimentos que confirmaram o resultado de Galileu. Desta forma, levando este fato experimental à segunda lei, a conclusão é uma identificação entre carga gravitacional e carga inercial, $m_{g}=m_{i}$. A ideia de carga gravitacional iniciou e terminou com Newton. Hoje falamos apenas em termos da massa inercial, simplesmente denotada por $m$. Einstein explorou este fato curioso para a elaboração de sua Teoria geral da Relatividade, a qual corrige a gravitação Newtoniana.
Alguns sistemas mecânicos tendo a gravidade como a força motriz serão discutidos nas subseções seguintes.
2.4. Queda livre
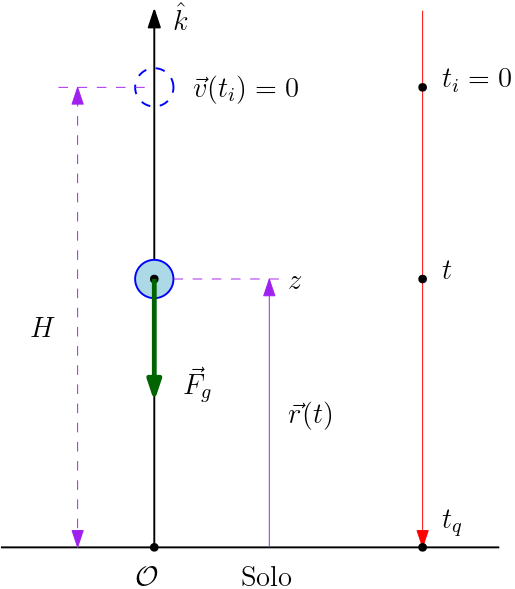
Solte do repouso, numa altura \(H\) acima do solo, um objeto de massa $m$. Este objeto está sujeito à ação da força da gravidade $\vec{F}_{g}$, dirigida ao solo. O solo está no plano XY. Como podemos verificar facilmente, a trajetória deste objeto será retilínea e
vertical (eixo Z), na qual o objeto atingirá o solo depois de algum instante. Esse fato nos sugere o sistema de coordenadas mostrado na Figura 1, onde escolhemos o eixo Z na direção da trajetória retilínea. Esta escolha é a mais simples possível.
A Figura 1 mostra o eixo temporal (meramente ilustrativo) em seu lado direito. No instante inicial $t_{i}=0$, o objeto está na altura $z(t_{i})=H$, com velocidade nula, $\vec{v}(t_{i})=0$. Quando o objeto é solto, ele entra em movimento (de "queda" ao
solo). A Figura 1 mostra também a posição $z(t)$ do objeto num instante $t>t_{i}$ qualquer. Quando o objeto atinge o solo, num instante $t_{q}$ (tempo de queda), naturalmente $z(t_{q})=0$. Este sistema mecânico é denominado de "queda livre". A única
força presente é a gravidade.
Estabelecido o melhor sistema de coordenadas (mostrado na Figura 1) e nomeado todos os parâmetros e quantidade vetoriais pertinentes, devemos escrever todos os vetores em coordenadas. Iniciando pelas condições iniciais ($t_{i}=0$), \begin{equation} \vec{r}(0)=H\hat{k},\quad \vec{v}(0)=0,\end{equation} e a força da gravidade,
\begin{equation}\vec{F}_{g}=-mg\,\hat{k},\quad g=9,8~\text{m}/\text{s}^{2}.\end{equation} Em seguida precisamos das quantidades cinemáticas num tempo qualquer $t>0$, \begin{equation}
\vec{r}(t)=z(t)\hat{k},\quad \vec{v}(t)=\dot{z}(t)\hat{k},\quad \vec{a}(t)=\ddot{z}(t)\hat{k}. \end{equation} Hora de usar a segunda lei $\vec{F}_{g}=m\vec{a}$ (massa constante) na forma de coordenadas, \begin{equation} -mg\,\hat{k}=m\ddot{z}(t)\hat{k} \implies \ddot{z}=-g,\end{equation} a qual implica em uma EDO fácil de ser resolvida. Esta EDO foi discutida na Seção Introito. Sua solução é \begin{equation} z(t)=c_{0}+c_{1}t-\frac{1}{2}gt^{2},\end{equation} cuja verificação é imediata (verifique). Assim, a componente Z do vetores velocidade e aceleração são \begin{equation} v_{z}(t)=\dot{z}(t)=c_{1}-gt,\quad a_{z}=\dot{v}_{z}=-g.\end{equation} As constantes $c_{0}$ e $c_{1}$ são determinadas pelas condições iniciais dadas, substituídas em $z(t)$ e $v_{z}(t)$, \begin{equation} v_{z}(0)=c_{1}=0\implies c_{1}=0,\end{equation} e \begin{equation} z(0)=c_{0}=H\implies c_{0}=H.\end{equation} Desta forma, a trajetória é a reta $\vec{r}(t)=z(t)\, \hat{k}$, com a equação horária \begin{equation} z(t)=H-\frac{1}{2}gt^{2}. \end{equation}
O tempo de queda $t_{q}$ é dado pelo condição (verifique) \begin{equation} z(t_{q})=H-\frac{1}{2}gt_{q}^{2}=0 \implies t_{q}=\sqrt{\frac{2H}{g}}. \end{equation} No momento em que toca o solo, a componente Z da velocidade do objeto é (verifique) \begin{equation} v_{z}(t_{q})=-\sqrt{2gH}. \end{equation} Esta é uma ótima oportunidade para checar o esquema de calcular o comprimento da trajetória entre os instantes inicial $t_{i}=0$ e final $t_{q}$, o qual sabemos ser $H$, \begin{equation}\Delta s=\int\limits_{t=0}^{t=t_{q}}\!|v_{z}(t)|\, dt=\left.\frac{g}{2}t^{2}\right|_{t=0}^{t=t_{q}}=H, \end{equation} como esperado (verifique). Note o detalhe na simplificação do módulo do vetor velocidade $\vec{v}(t)=v_{z}(t)\hat{k}$ (verifique), \begin{equation} v(t)=\|\vec{v}(t)\|= \sqrt{\vec{v}\cdot\vec{v}}= \sqrt{v_{z}^{2}(t)}= |v_{z}(t)|=gt. \end{equation}
Exercícios. Detalhe todas as passagens sinalizadas por "verifique".
2.5. Lançamento oblíquo
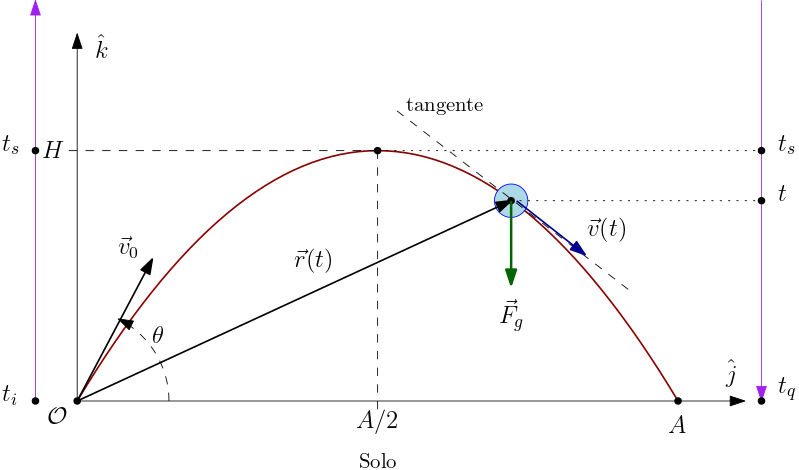
No lançamento oblíquo, um objeto de massa \(m\), sob ação da gravidade $\vec{F}_{g}$, dirigida ao solo, é lançado com uma determinada velocidade inicial $\vec{v}_{0}$. O experimento mostra uma trajetória plana com curvatura. Sendo plana, podemos colocá-la
no plano YZ, por conveniência, com o eixo Z perpendicular ao solo (plano XY). Essa é a melhor escolha para o sistema de coordenadas nesse caso, a qual está ilustrada na Figura 1.
A Figura 1 exibe o vetor velocidade inicial $\vec{v}_{0}=\vec{v}(t_{i})$, o qual faz um ângulo $\theta$ ($0\leq\theta\leq\pi$) com o eixo Y (no solo). Por conveniência, escolheremos o instante inicial como sendo zero, $t_{i}=0$. Também por conveniência, escolheremos a origem como a posição inicial, $\vec{r}(t_{i})=0$. A Figura 1 exibe também o vetor posição $\vec{r}(t)$ no instante $t>t_{i}$, bem como o vetor velocidade neste mesmo instante. Lembre-se que a velocidade é sempre tangente à trajetória (mesmo que a curva representando a trajetória ainda não seja conhecida).
Escreva todos os vetores em coordenadas. Usando o sistema de coordenadas mostrado na Figura 1, temos a gravidade \begin{equation} \vec{F}_{g}=-mg\,\hat{k},\; g=9,8~\text{m}/\text{s}^{2}, \end{equation} o vetor posição \begin{equation} \vec{r}(t)=x(t)\hat{i}+y(t)\hat{j}+z(t)\hat{k},
\end{equation} o vetor velocidade \begin{equation} \vec{v}(t)=\dot{x}(t)\hat{i}+\dot{y}(t)\hat{j}+\dot{z}(t)\hat{k}, \end{equation} e o vetor aceleração \begin{equation} \vec{a}(t)=\ddot{x}(t)\hat{i}+\ddot{y}(t)\hat{j}+\ddot{z}(t)\hat{k}. \end{equation}
Finalmente, as condições iniciais, \begin{equation} x(0)=y(0)=z(0)=0 \end{equation} e \begin{equation} \dot{x}(0)=0, \dot{y}(0)=v_{0}\cos\theta, \dot{z}(0)=v_{0}\sin\theta. \end{equation}
Momento de usar a segunda lei $\vec{F}_{g}=m\vec{a}$ (massa constante) na forma de coordenadas, \begin{equation} -mg\,\hat{k}= m\ddot{x}(t)\hat{i}+ m\ddot{y}(t)\hat{j}+ m\ddot{z}(t)\hat{k}, \end{equation} a qual implica em três EDOs (a igualdade vetorial
implica na igualdade entre coordenadas em cada eixo; verifique), \begin{equation} 0=\ddot{x}(t),\; 0=\ddot{y}(t),\; -g=\ddot{z}(t). \end{equation} Essas EDOs são, essencialmente, do mesmo tipo: derivada segunda igual a uma constante. De acordo com a Seção Introito, cada equação horária será um polinômio no tempo $t$ (verifique), \begin{align} x(t) &= c_{1}+c_{2}t,\\ y(t) &= c_{3}+c_{4}t,\\ z(t) &= c_{5}+c_{6}t-\frac{1}{2}gt^{2}. \end{align} As seis coordenadas serão
determinadas pelas condições iniciais (verifique), \begin{equation} c_{1}=c_{3}=c_{5}=0, \end{equation} e \begin{equation} c_{2}=0, c_{4}=v_{0}\cos\theta, c_{6}=v_{0}\sin\theta. \end{equation}
Desta forma, esta trajetória é representada pela curva cuja forma
paramétrica é dada pelas equações horárias
\begin{align}
x(t) &= 0,\\
y(t) &= v_{0}\cos\theta\, t,\\
z(t) &= v_{0}\sin\theta\, t-\frac{1}{2}gt^{2}.
\end{align}
Esta curva é uma parábola no plano YZ. Consequentemente, as
componentes do vetor velocidade são,
\begin{align}
v_x(t) &= 0,\\
v_y(t) &= v_{0}\cos\theta,\\
v_z(t) &= v_{0}\sin\theta-gt.
\end{align}
O módulo desse vetor velocidade, necessário para calcular o
comprimento da trajetória, é (verifique)
\begin{equation}
v^{2}(t)=\vec{v}\cdot\vec{v}= v_{0}^{2}-2v_{0}\sin\theta\, gt +(gt)^2.
\end{equation}
Como o comprimento da trajetória é a integral do módulo do vetor
velocidade
\begin{equation}
\Delta s=\int\limits_{t=0}^{t=t_{q}}\! v(t)\, dt=f(\theta),
\end{equation}
ele se torna uma função do ângulo $\theta$ de lançamento. Assim, o
maior comprimento ocorre para um ângulo $\theta_{m}$ quando esta
função $f(\theta)$ passa pelo seu máximo (um dos extremos),
satisfazendo (verifique)
\begin{equation}
\left.\frac{df}{d\theta}\right|_{\theta=\theta_{m}}=0 \implies
\theta_{m}=\frac{\pi}{2}.
\end{equation}
Esse também é o ângulo para o qual o alcance é máximo (verifique).
Dica: use o fato da derivada de uma função composta (como a raiz quadrada) ser proporcional à derivada de seu argumento.
Modelagem. Apenas observando o experimento é impossível afirmar que a trajetória de um objeto lançado obliquamente é uma parábola. Mais difícil ainda identificar o ângulo para o qual o alcance (e o comprimento da trajetória) é máximo. Quando o sistema mecânico é simulado por um modelo matemático, previsões podem ser feitas sem a necessidade de experimentos. Como a força resultante é paralela ao eixo vertical, o eixo Z, a segunda lei nos diz que o momentum linear é conservado nas demais direções (onde as componentes da força resultante são nulas). A conservação do momentum linear no eixo X é trivial, pois não há movimento lá. No entanto, a conservação do momentum linear no eixo Y, mais uma previsão do modelo matemático, somente pode ser observada após uma série de medidas cuidadosas da velocidade neste eixo. Outro resultado que jamais poderia ser percebido somente pela experimentação: a trajetória não depende da massa do objeto. Isto significa que as trajetórias de uma bola de gude e de um fusca serão idênticas quando lançados sob as mesmas condições iniciais. Este modelo (ainda) não leva em consideração a presença da atmosfera (se houver).
Exercícios. Detalhe todas as passagens sinalizadas por "verifique''.
2.6. Oscilador harmônico
Lei de Hooke. Por volta de 1660 Hooke descobriu experimentalmente o comportamento da deformação de objetos. Quando deformado, comprimido ou esticado, o objeto tende a se restaurar. Para pequenas
deformações, a restauração é proporcional à deformação. Essa é a lei de Hooke. Na mesma época, Newton estava estabelecendo suas leis do movimento, bem como a teoria da gravitação. Hoje podemos parafrasear a lei de Hooke em termos de forças, as mesmas
que aparecem na segunda lei: a força restauradora produzida por uma pequena deformação em um objeto é proporcional à deformação e está na mesma direção da deformação. A lei de Hooke permitiu a construção de molas com as mais variadas capacidades restauradoras
e formatos. A capacidade de restauração de uma mola é dada pela chamada constante de mola \(k\), determinada experimentalmente.
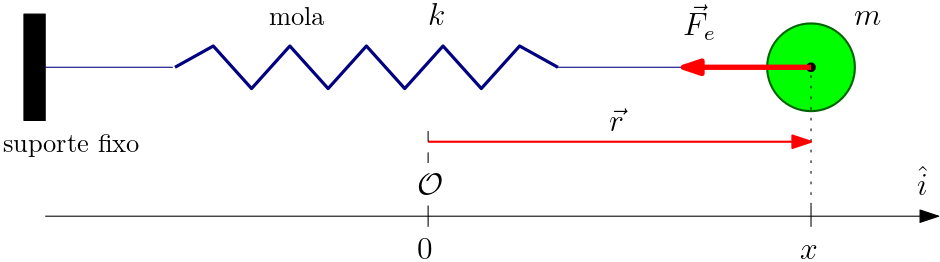
Força elástica. A Figura 1 mostra uma mola de constante $k>0$, em forma de uma espiral. Uma das extremidades está presa no suporte mantido fixo (lado esquerdo). Na outra extremidade da mola há um objeto de massa $m$, o qual é permitido movimentar-se na direção da deformação. Esse sistema mecânico é denominado de massa-mola. O sistema de coordenadas mais adequado está mostrado na Figura 1, onde a deformação está em um dos eixos e a origem $\mathcal{O}$ corresponde a uma deformação nula na mola. Desta forma, a posição $x$ do objeto de massa $m$ também indica a deformação aplicada à mola. Para $x>0$ a mola está esticada (situação indicada na figura). Para $x<0$ a mola está comprimida. Assim a lei de Hooke toma a forma \begin{equation} \vec{F}_{e}=-kx\,\hat{i}. \end{equation} Note esta força elástica é dependente da posição $x$ da massa presa à mola e sempre oposta à deformação ($|x|$) graças ao sinal negativo presente nela (verifique). A constante de mola $k$ é sempre positiva.
Fatos experimentais. A observação cuidadosa do sistema massa-mola exibido na Figura 1, completamente isolado, revela os seguintes fatos.
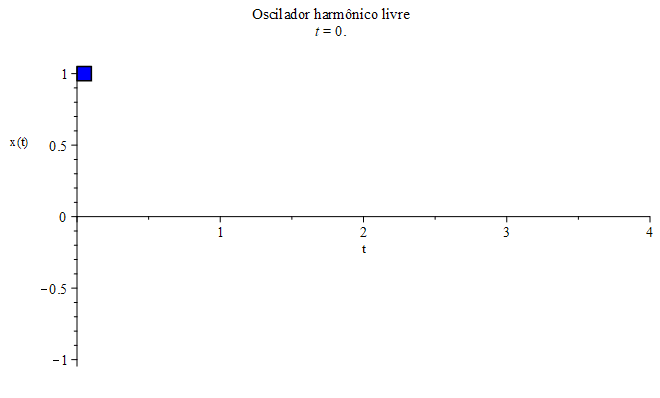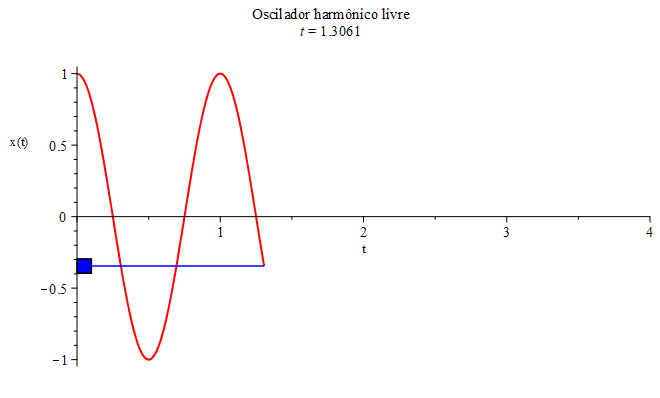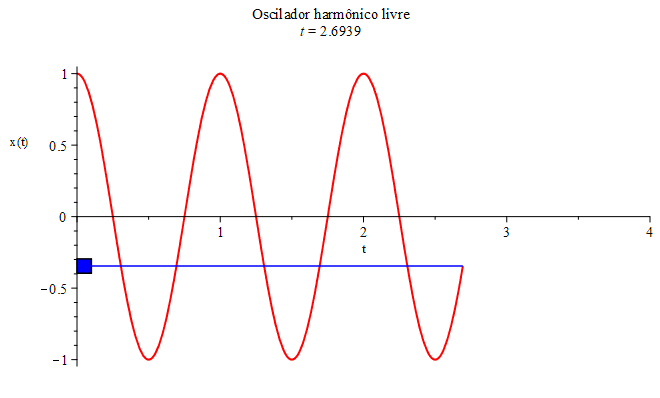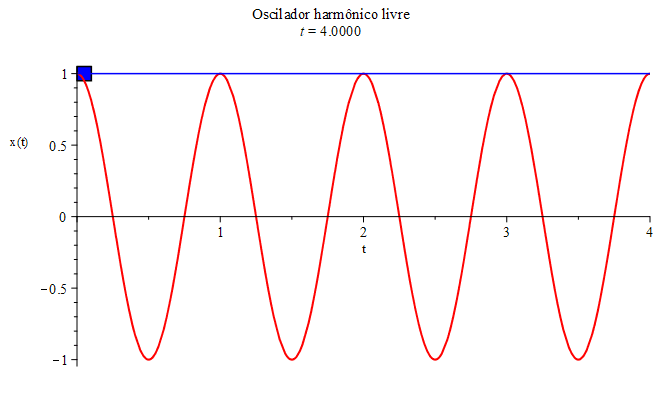
- A massa $m$ executa um movimento oscilatório, limitado a uma certa região retilínea de comprimento $2A$, como mostrado na Figura 2 (com $A=1$). A quantidade $A$ é denominada de amplitude.
- Esse movimento oscilatório tem uma frequência (fixa) que depende apenas da massa $m$ e da constante de mola $k$. A frequência não depende da amplitude.
- Na ausência de outras forças, esse movimento oscilatório é permanente, harmônico. Porém, na presença da atmosfera, a qual contribui com uma força viscosa, esse movimento cessa.
Segunda lei. A Figura 1 representa a massa sujeita à força elástica $\vec{F}_{e}$ num dado instante de tempo $t$ após o momento inicial $t_{0}$. Neste instante $t$, a massa $m$ encontra-se
numa determinada posição especificada pelo vetor posição $\vec{r}$, cuja única componente é $x$ (sabemos que a trajetória será retilínea). Portanto, os vetores cinemáticos, escritos em coordenadas, no mesmo sistema de coordenadas $\mathcal{O}$
em que a força elástica foi escrita, são \begin{equation} \vec{r}=x\,\hat{i},\; \vec{v}=\dot{x}\,\hat{i},\; \vec{a}=\ddot{x}\,\hat{i}. \end{equation} desta forma, a segunda lei $\vec{F}_{e}=\dot{\vec{p}}=m\vec{a}$ (massa constante), fornece a seguinte
EDO (verifique): \begin{equation} -kx=m\ddot{x} \implies \ddot{x}=-\omega_{0}^{2}\,x,\; \omega_{0}=\sqrt{\frac{k}{m}}.\end{equation} Note que a constante (ou parâmetro) $\omega_{0}$ tem dimensões de frequência (inverso do tempo; verifique),
\begin{equation} [k]=\frac{M}{T^{2}},\quad [\omega_{0}]=\frac{1}{T}.\end{equation}
Equação horária. Essa EDO está nos perguntando se conhecemos "uma função cuja derivada segunda é proporcional a ela mesma". Note que essa constante de proporcionalidade é estritamente negativa,
$-\omega_{0}^{2}$. Sim, conhecemos as funções trigonométricas (seno e cosseno). Assim, a equação horária pode ser da forma \begin{equation} x(t)=A\cos\theta(t), \end{equation} com $A$ constante e $\theta(t)$ uma função ainda desconhecida do tempo. Lembre-se
que o cosseno é uma função transcendental e, como tal, seu argumento deve ser adimensional. Portanto, $[A]=[x]=L$. Tomemos a derivada segunda (verifique) dessa equação horária (proposta de solução), sem esquecer que as funções trigonométricas
são funções compostas, \begin{equation} \dot{x}=-A\dot{\theta}\sin\theta,\quad \ddot{x}=-A\,\dot{\theta}^{2}\cos\theta-A\,\ddot{\theta}\sin\theta.\end{equation} Momento de substituir (verifique) a derivada segunda na EDO, \begin{equation} \ddot{x}=-\omega_{0}^{2}\,x
\implies \dot{\theta}^{2}\cos\theta+\ddot{\theta}\sin\theta=\omega_{0}^{2}\cos\theta.\end{equation} Este resultado pode ser reescrito numa forma mais organizada, coletando os termos em cosseno e seno, (verifique) \begin{equation} (\dot{\theta}^{2}-\omega_{0}^{2})\cos\theta+\ddot{\theta}A\sin\theta=0.\end{equation}
A trigonometria nos ensinou que uma função trigonométrica não pode ser escrita como múltipla da outra, ou seja, as funções cosseno e seno são linearmente independentes, \begin{equation} a\cos\theta+b\sin\theta=0 \implies a=b=0.\end{equation} A expressão
que obtivemos anteriormente, decorrente da substituição da equação horária proposta na EDO do sistema massa-mola, é justamente uma combinação linear de duas funções linearmente independentes. Portanto, cada coeficiente nesta equação deve ser nulo (única
solução possível), \begin{equation} \dot{\theta}^{2}-\omega_{0}^{2}=0,\quad \ddot{\theta}=0.\end{equation} A última dessas duas EDOs para a função $\theta(t)$, denominada de fase (argumento de uma
função trigonométrica), implica que ela seja uma função linear do tempo (verifique), \begin{equation} \ddot{\theta}=0 \implies \theta(t)=\varphi+\omega t \implies \dot{\theta}=\omega,\end{equation} com $\varphi$ e $\omega$ constantes. Substituindo
esse resultado na outra EDO para $\theta$, encontramos (verifique) o valor da constante $\omega$, \begin{equation} \dot{\theta}^{2}-\omega_{0}^{2}=0 \implies \dot{\theta}^{2}=\omega^{2}\omega_{0}^{2} \implies \omega=\pm \omega_{0}.\end{equation}
Como as funções trigonométricas possuem paridades bem definidas (o cosseno é uma função par e o seno é uma função ímpar) e $A$ e $\varphi$ são arbitrárias (o que significa que podemos reescrevê-las como $-A$ e $-\varphi$), podemos ignorar (verifique)
o sinal o negativo em $\omega=\pm \omega_{0}$. Assim, a equação horária $x(t)$, solução da EDO do sistema massa-mola, é \begin{equation}\ddot{x}=-\omega_{0}^{2}\,x \implies x(t)=A\cos\theta(t),\; \theta(t)=\varphi+\omega_{0} t.\end{equation} Por razões
óbvias, a constante $A$ é denominada de amplitude, $\varphi$ de constante da fase e $\omega_{0}$ de frequência (angular) natural.
Essa EDO do sistema massa-mola aparece em muitos outros modelos em diversas áreas do conhecimento. Ela deve ser memorizada.
Condições iniciais. As duas constantes $A$ (amplitude) e $\varphi$ (constante da fase) devem ser determinadas pelas condições iniciais. Por exemplo, suponha que no instante inicial $t_{0}=0$ a massa $m$ seja solta do repouso, portanto com velocidade inicial nula, $\dot{x}(0)=0$, na posição $x(0)=1$ (uma unidade de comprimento). Impondo que a velocidade inicial seja nula (repouso), determinamos a constante da fase, \begin{equation}\dot{x}(0)=-\omega_{0}A\sin\varphi=0\implies \varphi=0. \end{equation} Com a constante da fase determinada, $\varphi=0$,
a posição inicial determina a amplitude, \begin{equation}x(0)=A\cos(0)=1\implies A=1.\end{equation} Escolhendo $\omega_{0}=1$ (inverso da unidade de tempo), a equação horária correspondente a este exemplo, $x(t)=cos(t)$ (em unidades de comprimento), está mostrada na Figura 2, juntamente com o movimento da massa $m$ em sua trajetória retilínea e oscilatória (na vertical, por comodidade). Esse sistema massa-mola também é conhecido por oscilador harmônico.
O adjetivo harmônico vem da presença de uma função trigonométrica elementar (periódica) na equação horária.
Modelagem. Naturalmente, a concordância entre a previsão feita pelo modelo matemático para a frequência de oscilação,\begin{equation} f=2\pi\omega_{0},\; \omega_{0}=\sqrt{\frac{k}{m}},\end{equation} e o valor medido experimentalmente é excelente, perfeita. Note o fator $2\pi$ na frequência que é medida no laboratório. A inclusão de uma força viscosa, produzida por um fluido, como a atmosfera ou óleo no caso de amortecedores, leva à indústria bilionário dos amortecedores.
Exercícios. Detalhe todas as passagens sinalizadas por "verifique".
2.7. Pêndulo
em breve
3. Energia
Energia em mecânica é um escalar, um número, que, sob certas condições, permanece constante, invariante, conservado, durante o movimento de um sistema mecânico. A compreensão do conceito de energia mecânica e sua importância levou séculos para amadurecer até a forma atual.
3.1. Energia cinética
Dada a força resultante \(\vec{F}\), a segunda lei de Newton $\vec{F}=\dot{\vec{p}}$ determina a trajetória resultante. O que resulta se integrarmos a projeção desta força ao longo desta trajetória? Vejamos: \begin{equation} \int\limits_{t_{0}}^{t} \vec{F}\cdot d\vec{r}= \int\limits_{t_{0}}^{t} \dot{\vec{p}}\cdot d\vec{r}= \int\limits_{t_{0}}^{t} \frac{d\vec{p}}{dt}\cdot d\vec{r}= \int\limits_{t_{0}}^{t} d\vec{p}\cdot \frac{d\vec{r}}{dt}=\int\limits_{t_{0}}^{t} \vec{v}\cdot d\vec{p}, \end{equation} onde escrevemos a derivada primeira como a razão entre duas diferenciais (quantidades infinitesimalmente pequenas), $\vec{v}=d\vec{r}/dt$, podendo a diferencial temporal $dt$ ser manipulada como qualquer expressão algébrica. Neste esquema, diferenciais atraem diferenciais. Considerando a massa $m$ constante, então $d\vec{p}=m\vec{v}$. Esta condição permite que a integral anterior possa ser calculada, \begin{equation} \int\limits_{t_{0}}^{t} \vec{F}\cdot d\vec{r}=m\int\limits_{t_{0}}^{t} \vec{v}\cdot d\vec{v}=\left.\frac{m}{2}\vec{v}\cdot\vec{v}\,\right|_{t_{0}}^{t}=\left.\frac{m}{2}v^{2}\right|_{t_{0}}^{t}.\end{equation} Note que o resultado dessa integral depende apenas dos valores do módulo (ao quadrado) do vetor velocidade no ponto de partida em $t_{0}$ e no ponto de chegada em $t$. Lembre-se que esse mesmo módulo do vetor velocidade, quando integrado, nós informa o comprimento da trajetória.
Devida à importância dessa integral, a quantidade \begin{equation} T=\frac{1}{2}mv^{2},\quad v^{2}=\vec{v}\cdot\vec{v}, \end{equation} será denominada de energia cinética. Ela é um número que varia ao longo da trajetória. É constante somente quando o módulo do vetor velocidade é constante, como no movimento circular, por exemplo.
Unidades. As dimensões de energia cinética são as dimensões de massa vezes velocidade ao quadrado, \begin{equation} [T]=\frac{ML^{2}}{T^{2}}.\end{equation} Note que são as mesmas dimensões de força vezes distância. No Sistema Internacional, $\text{kg}\,\text{m}^{2}/\text{s}^{2}=\text{J}$ foi denominada de Joule, em homenagem ao descobridor da equivalência entre energia térmica e energia mecânica.
3.2. Trabalho
A definição de energia cinética implica que a integral da projeção da força ao longo de uma trajetória, mesmo sendo qualquer, é também importante, por isso deve receber um nome: \(\) \begin{equation} \Delta W=\int\limits_{t_{0}}^{t} \vec{F}\cdot d\vec{r}. \end{equation} Em mecânica, este número foi denominado de trabalho. Em matemática, ele foi denominado de circuitação (ou circulação) do campo vetorial $\vec{F}$. Importante frisar que a trajetória pode ser escolhida livremente, ou
seja, a trajetória aqui não precisa ser aquela determinada pela força
resultante. O vetor $d\vec{r}$ é sempre tangente à trajetória escolhida, representada parametricamente pelo vetor posição $\vec{r}$.
Esta integral, ou o trabalho, tem dois ingredientes que caracterizam completamente um movimento: a força resultante $\vec{F}$ e o vetor tangente $d\vec{r}$ à trajetória escolhida. Não é um exagero afirmar que esta integral representa o "custo" desse movimento. No caso, um custo energético. De fato, usando a definição de energia cinética, o custo de se movimentar desde o ponto de partida em $t_{0}$ até o ponto de chegada em $t$ é dado pela variação de energia cinética correspondente, \begin{equation} \Delta W=\int\limits_{t_{0}}^{t} \vec{F}\cdot d\vec{r}=\Delta T,\quad T=\frac{1}{2}mv^{2}. \end{equation} Esse resultado também é conhecido por teorema do trabalho-energia cinética.
Importante: ao contrário da energia cinética, o trabalho não pertence ao objeto em movimento. A energia cinética pertence ao objeto, pois depende apenas da velocidade e da massa do objeto. Assim, podemos dizer que um objeto em movimento possui energia cinética. No entanto, não podemos dizer que um objeto em movimento possui trabalho, pois o trabalho depende também da trajetória. Naturalmente, trabalho e energia cinética possuem as mesmas dimensões. Porém trabalho e energia cinética são quantidades diferentes. No máximo, podemos interpretar uma variação de trabalho como o processo pelo qual o objeto ganha ou perde uma variação de energia cinética numericamente igual a esta variação de trabalho. Trabalho é um processo de troca de energia.
3.3. Energia potencial
Podemos classificar forças em dois tipos: aquelas que deixam o trabalho \(\) \begin{equation} \Delta W=\int\limits_{t_{0}}^{t} \vec{F}\cdot d\vec{r}, \end{equation} independente da trajetória e aquelas que deixam o trabalho dependente da trajetória. As forças que deixam o trabalho independente da trajetória são denominadas de forças conservativas (por
razões óbvias vistas a seguir). Portanto, para as forças conservativas, o trabalho depende apenas dos pontos inicial e final. Isto implica em um trabalho nulo numa trajetória fechada, \begin{equation} \Delta W=\oint \vec{F}\cdot d\vec{r}=0. \end{equation}
Esta integral numa trajetória fechada igual a zero é uma definição matemática de uma força conservativa.
Como o trabalho de uma força conservativa é uma função (escalar) da posição $\vec{r}$, podemos rebatizá-lo de energia potencial, \begin{equation} V=-\int \vec{F}\cdot d\vec{r}=V(\vec{r}), \end{equation}
onde o sinal negativo foi introduzido por mera conveniência. Também por conveniência, a integral aqui pode ser efetuado de forma indefinida. Isto significa que energia potencial, ao contrário da energia cinética, está definida a menos de uma constante
arbitrária (vinda da integração). Importante: a energia potencial somente pode ser definida para forças conservativas, onde o trabalho torna-se uma função da posição. Não existe a definição de energia potencial para forças não-conservativas.
Dado o teorema fundamental do cálculo, estabelecendo uma relação entre derivada e integral, ao tomarmos uma derivada (espacial) da energia potencial devemos obter o integrando. Do ponto de vista técnico, podemos tomar derivadas espaciais em cada uma das
três direções espaciais, ou em relação a cada uma das componentes $x_{i}$ do vetor posição $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ num sistema de coordenadas ortonormal. A implementação aqui deste teorema fundamental é feita definindo o operador vetorial,
\begin{equation} \vec{\nabla}=\hat{i}\frac{\partial}{\partial x}+\hat{j}\frac{\partial}{\partial y}+\hat{k}\frac{\partial}{\partial z}, \end{equation} denominado de gradiente. O operador vetorial
gradiente atua em funções da posição, como nossa energia potencial, \begin{equation} \vec{\nabla}V(\vec{r})=\hat{i}\frac{\partial V}{\partial x}+\hat{j}\frac{\partial V}{\partial y}+\hat{k}\frac{\partial V}{\partial z}, \end{equation} produzindo um
vetor (um campo vetorial em geral). Além das regras usuais de derivadas, a derivada parcial $\partial/\partial x$ considera as outras variáveis $y$ e $z$ como constantes. Portanto, o teorema fundamental pode ser estabelecido:
- Teorema 4
- Dada a energia potencial $V(\vec{r})$, a força conservativa associada é \begin{equation}\vec{F}=-\vec{\nabla}V(\vec{r}). \end{equation}
O Teorema 4 mostra claramente porque a energia potencial pode ser definida com uma constante aditiva: quando se precisa dela é via derivadas espaciais que eliminam qualquer constante aditiva. Desta forma, podemos escolher um valor para a energia potencial em algum lugar do espaço e determinar a constante aditiva como consequência desta escolha. Vale observar o papel fundamental da energia potencial: é um campo escalar cujas variações espaciais geram uma força (um campo vetorial). Do ponto de vista computacional é mais econômico guardar a energia potencial, por ser um campo escalar (uma informação), do que a força, um campo vetorial (três informações). A mudança do caráter escalar para vetorial é efetuada pelo operador gradiente (também de baixo custo computacional).
3.4. Energia mecânica
Considerando o teorema do trabalho-energia cinética e a variação da energia potencial como menos a variação de trabalho, temos \(\) \begin{equation} \Delta W=\Delta T\;\text{e}\; \Delta W=-\Delta V \implies \Delta(T+V)=0. \end{equation} Esta é a razão para termos definido
a energia potencial com o sinal negativo em evidência: para que a soma de energias $T+V$ seja constante. Esta soma é denominada de energia mecânica, \begin{equation} E=T+V,\quad T=\frac{1}{2}mv^{2},\quad V=-\int \vec{F}\cdot d\vec{r}. \end{equation}
- Teorema 5
- Em um sistema contendo apenas forças conservativas, a energia mecânica é constante $\dot{E}=0$, $E=T+V$.
Esse Teorema 5 confere o adjetivo "conservativo" às forças que produzem um trabalho nulo numa trajetória fechada, quesito básico para se definir a energia potencial e, portanto, a energia mecânica. A energia mecânica é um número constante (conservado) durante o movimento produzido por uma força conservativa. Esta quantidade escalar conservada levou séculos para ser descoberta. A conservação da energia mecânica (Teorema 5) e do momentum linear (Teorema 1) constituem as leis de conservação para o movimento de translação.
As forças fundamentais na nossa natureza são conservativas. Entre elas, temos explorado a força gravitacional logo acima da superfície terrestre (a gravidade). A força elástica (de origem eletromagnética) também é conservativa. Por outro lado, qualquer força dependente da velocidade, como a força viscosa, não é conservativa. Basta a presença de uma única força não-conservativa em um sistema mecânico, mesmo contendo outras forças conservativas, para quebrar a conservação da energia mecânica. Em sistemas não-conservativos, a energia mecânica é transformada em outros tipos de energia, como térmica, por exemplo, muito comum na presença de atrito e viscosidade. Para constar, potência é a taxa de variação temporal de uma dada energia.
A conservação da energia mecânica implica numa troca instantânea entre as energias cinética e potencial. O trabalho é o processo que quantifica essas trocas de energias. Por isso não podemos interpretar o trabalho como algo pertencente a um objeto ou a um sistema mecânico. A energia cinética pertence a um objeto (com velocidade) e a energia potencial pertence ao sistema mecânico. Alguns casos são comentados a seguir.
Lançamento oblíquo. Considerando a trajetória parabólica no lançamento oblíquo discutido na Seção 2.5, \begin{equation} x(t) = 0,\quad y(t) = v_{0}\cos(\theta)\, t,\quad z(t) = v_{0}\sin(\theta)\, t-\frac{1}{2}gt^{2}, \end{equation} produzida pela força $\vec{F}_{g}=-mg\,\hat{k}$, podemos calcular a energia mecânica deste sistema. O módulo (ao quadrado) do vetor velocidade é \begin{equation} v^{2}(t)=\vec{v}\cdot\vec{v}= v_{0}^{2}-2v_{0}\sin(\theta)\,g t +(gt)^2, \end{equation} e a energia cinética correspondente é \begin{equation} T(t)=\frac{1}{2}mv^{2}(t)= \frac{1}{2}mv_{0}^{2}-mg\,v_{0}\sin(\theta)\, t +\frac{1}{2}mg\,gt^2. \end{equation} A energia potencial é dada pela integral da projeção da força peso ao longo da trajetória, \begin{equation} -\vec{F}_{g}\cdot d\vec{r}=-(-mg\,\hat{k})\cdot(dx\hat{i}+dy\hat{j}+dz\hat{k})=mg\,dz, \end{equation} que pode ser integrada ao longo do eixo Z (verifique), \begin{equation} V=-\int\vec{F}_{g}\cdot d\vec{r}=mg\int\,dz=mg\,z +C=V(z),\end{equation} onde $C$ é uma constante arbitrária. Para vermos a dependência explicita da energia potencial com o tempo, devemos usar a equação horária $z(t)$, \begin{equation} V(t)=mg\,z(t) +C=mg\,v_{0}\sin(\theta)\, t-\frac{1}{2}mg\,gt^{2}+C.\end{equation} Note como a energia potencial é uma função linear da coordenada $z$, a altura acima do solo (plano XY), e somente desta coordenada. Com a escolha $C=0$, esta energia potencial é nula no plano XY e máxima na altura máxima $z=H$. Mesma com as energias cinética e potencial variando um função do tempo (ou da posição), a energia mecânica torna-se uma quantidade conservada, \begin{equation} E=T(t)+V(t)=\frac{1}{2}mv_{0}^{2}+C. \end{equation} A constante arbitrária pode ser escolhida como zero no instante inicial. Assim, a energia mecânica deste sistema é constante e igual (naturalmente) à energia cinética inicial. Resta reobter a força peso a partir da energia potencial (verifique), \begin{equation} \vec{F}_{g}=-\vec{\nabla}V=-\frac{dV}{dz}\,\hat{k}=-mg\,\hat{k}. \end{equation}
Oscilador harmônico. Consideremos agora o sistema massa-mola discutido na Seção 2.6. O movimento está inteiramente ao longo do eixo X, com a equação horária \begin{equation} x(t)=A\cos\theta(t),\quad \theta(t)=\varphi+\omega_{0} t, \end{equation} criada pela força elástica $\vec{F}_{e}=-kx\,\hat{i}$. A energia cinética é (verifique) \begin{equation}
T(t)=\frac{1}{2}mv^{2}(t)= \frac{1}{2}m\omega_{0}^{2}A^{2}\sin^{2}\theta(t)=\frac{1}{2}kA^{2}\sin^{2}\theta(t). \end{equation} A energia potencial é (verifique) \begin{equation} V=-\int\vec{F}_{e}\cdot d\vec{r}=-\int(-kx\,\hat{i})\cdot(dx\hat{i}+dy\hat{j}+dz\hat{k})=k\int xdx= \frac{1}{2}k\,x^{2}+C=V(x). \end{equation} A constante arbitrária $C$ pode ser escolhida como zero para termos uma energia potencial elástica nula quando a mola não é deformada ($x=0$), \begin{equation} V(t)= \frac{1}{2}k\,x^{2}(t)=\frac{1}{2}k A^{2}\cos^{2}\theta(t).\end{equation} Desta forma a energia mecânica é conservada \begin{equation} E=T(t)+V(t)=\frac{1}{2}kA^{2}. \end{equation} Note que esta energia mecânica é numericamente igual à energia potencial elástica com o objeto na posição extrema $x=\pm A$, no instante em que sua velocidade é momentaneamente nula. Quando a mola não está deformada, $x=0$, a energia mecânica é composta somente pela sua energia cinética. Faça um gráfico mostrando estas três energias como funções do tempo (verifique). Resta reobter a força elástica a partir da energia potencial (verifique), \begin{equation} \vec{F}_{e}=-\vec{\nabla}V=-\frac{dV}{dx}\,\hat{i}=-kx\,\hat{i}. \end{equation}
Exercícios. Detalhe todas as passagens sinalizadas por "verifique".
4. Apêndices
em breve
4.1. Campos
Um campo é uma regra para pregar números (escalares), vetores e outros objetos numa dada posição do espaço. Um campo escalar é uma função da posição: dado uma posição, esta função fornece um valor numérico. Um campo vetorial, por sua vez, cria vetores específicos numa dada posição espacial. Por exemplo, a força gravitacional, criada pelo Newton, estabelece o vetor força \(\vec{F}\) sentido por um objeto de massa $m$ (corpo teste), \begin{equation} \vec{F}=G\frac{Mm}{r^{2}}\,\hat{r},\end{equation} colocado a uma distância $r$ do centro do objeto de massa $M$ (a fonte da força gravitacional). O versor $\hat{r}$ é radial, da fonte para o corpo teste. $G$ é a constante universal da gravitação. Essa força gravitacional é um campo vetorial. Seu módulo é um campo escalar. Note que, esta força é sempre perpendicular a uma superfície esférica de raio $r$ centrada na fonte e que a intensidade desta força tem o mesmo valor em qualquer posição nesta superfície esférica. Esse campo vetorial tem simetria radial (ou esférica).