MAT0234 Medida e Integração

Advertência: a seguinte lista  de tópicos será quase toda desenvolvida nesta ordem cronológica. Mas alguns temas podem não seguir a ordem.

0. Introdução: a noção de integral de Riemann 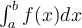$\int_a^b f(x) dx$

e a de Lebesgue. A noção de medida de um conjunto (intervalo, retângulo, paralelepípedo). 

Pré-requisitos: a. Axioma da Escolha e Princípio de Boa Ordem;

                           b. cardinalidade. Cardinal de N, de R e de Partes(X). Teorema de Cantor-Bernstein-Schröder

1. Impossibilidade de definir uma medida invariante por translações, com medida de (a,b) = b-a e sigma aditiva em Partes (R). Necessidade de se restringir a uma classe conjuntos menor. Anéis, álgebras, sigma anéis e sigma álgebras. Exemplos em R, R^2, S^1, S^2.  Sigma álgebra dos Borelianos.

2. funções mensuráveis. Mensurabilidade de f+g, c f, fg, sup(fn), inf (fn) , lim sup fn, lim inf fn, Lim fn. Decomposição de f em parte positiva e parte negativa.

3. Definição de medida. Definição de medida em uma álgebra e extensão para uma sigma álgebra. Medida Exterior. Medida Completa. Sigma álgebra dos conjuntos Lebesgue mensuráveis. Teorema de Carathéodory. 

4. Espaços de medida, funções simples e integração. Integração de funções mensuráveis.

5. Lema de Fatou; Teorema da convergência monótona; Teorema de convergência dominada. E outros.

6. A relação da integral de Lebesgue na reta com a integral de Riemann e com a integral imprópria de Riemann.

7. Aplicações do teorema de convergência dominada: derivação sob o sinal de integral, etc.

8. Conjuntos de Cantor e de Borel. Conjuntos não mensuráveis.

9. Espaços L^p; desigualdades de Hölder e Minkowski; completude dos espaços L^p. 

10. Modos de convergência (em todo ponto, em quase todo ponto, em medida, quase uniforme, em L^p).  Teorema de Lusin.

11. Medida Produto. Teoremas de Fubini e Tonelli para medida de Lebesgue em R^n. 

12. Tópicos opcionais