Anterior
Próximo

4. Indução

4.1. Ampère

 Oersted descobriu experimentalmente em 1820 que um fio transportando uma corrente elétrica produzia um campo magnético. Ele usou uma bússola para identificar (após três anos) que este campo magnético era circular ao fio, como vimos na Seção 3.2. Na época, definia-se campo magnético pela interação com uma bússola. Ímãs erão conhecidos há muito tempo e interagiam com bússolas (contendo também um ímã). Este experimento de Oersted mostrou pela primeira vez uma relação explícita entre os fenômenos elétricos (corrente) é magnéticos (ímãs). Uma simulação desse experimento pode ser vista abaixo (ou aqui) na aba eletroímã.


 Ampère nasceu em uma família rica e teve sua educação inteiramente em sua casa. Tornou-se professor de Matemática, Física e Química. Ainda em 1820 tomou conhecimento do experimento de Oersted e se dedicou a ele com tanto afinco ao ponto de traduzi-lo matematicamente no que chamamos hoje de lei de Ampère, corretíssima para correntes estáticas. Infelizmente ele não registrou seus passos nesta empreitada, publicou apenas seus resultados (de forma completa em 1826, um ano antes de sua morte). Ampére chegou a conjecturar cargas elétricas em movimento como a origem de campos magnéticos, quase um século antes do advento da Teoria da Relatividade Especial. Mais detalhes sobre Ampère podem ser obtidos aqui.

 Ampère foi capaz de mostrar que a circulação do campo magnético \(\vec{B}\) de uma corrente elétrica $I$ (estática; que não varia no tempo) em um fio retilíneo, circulação em torno desse fio, é proporcional à corrente elétrica que ele transporta:

\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}= 4C_{m}\, I,\quad C_{m}=\frac{\mu_{0}}{4\pi}.\end{equation}

Este resultado é válido sempre e é conhecido por lei de Ampère, o análogo à lei de Gauss para o campo elétrico. A curva fechada sobre a qual a circulação é calculada é a "curva amperiana".

 Usando os teoremas do Apêndice 2, podemos estabelecer uma versão local para a lei de Ampère,

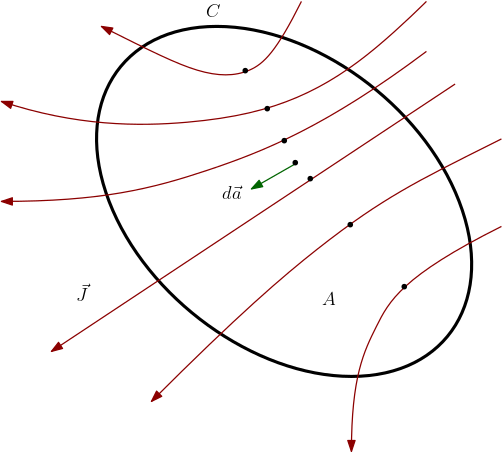
\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}= \int\limits_{A}\vec{\nabla}\times\vec{B}\cdot d\vec{a}= 4C_{m}\, I=4C_{m}\, \int\limits_{A}\vec{J}\cdot d\vec{a}\;\implies\; \vec{\nabla}\times\vec{B}=4C_{m}\vec{J},\end{equation}

onde o campo vetorial densidade de corrente $\vec{J}$ foi introduzido na Seção 3.3 (veja a Figura 2 na Tabela 1). Maxwell em 1861 notou que este resultado é compatível com a equação da continuidade (derivada na Seção 3.3) somente para campos estático (independentes do tempo), pois

\begin{equation} 0=\vec{\nabla}\cdot\vec{\nabla}\times\vec{B}=4C_{m}\vec{\nabla}\cdot\vec{J}= -4C_{m}\frac{\partial\rho}{\partial t},\end{equation}

onde $\rho$ é a densidade de cargas elétricas (dependente da posição e do tempo). A primeira igualdade é válida sempre ($\vec{\nabla}\cdot\vec{\nabla}=0$). Desta forma, Maxwell "corrigiu" a lei de Ampère (local) para

\begin{equation} \vec{\nabla}\times\vec{B}=4C_{m}\vec{J}+\frac{C_{m}}{C_{e}}\frac{\partial\vec{E}}{\partial t},\end{equation}

obtendo assim a terceira equação de Maxwell. Note que a variação espacial do campo magnético está relacionada com a variação temporal do campo elétrico. É um campo induzindo outro.

Exercício 1. Como ao usar a lei de Gauss, use argumentos de simetria e a lei de  Ampère para obter o campo magnético produzido por uma corrente $I$ (estática) em um fio retilíneo.

Exercício 2. Aplique o divergente na terceira equação de Maxwell e mostre que ela  é consistente com a primeira equação de Maxwell e com a equação da  continuidade.


Tab. 1: campo magnético de um fio e densidade de corrente.
Figura 1
Figura 2


Anterior
Próximo