7600107 - Física III (2020)

Gradiente. Considerando um campo escalar \(\phi=\phi(x,y,z)\), a sua diferencial (total) é

\(\displaystyle d\phi=\frac{\partial\phi}{\partial x}dx+ \frac{\partial\phi}{\partial y}dy+ \frac{\partial\phi}{\partial y}dy= \vec{\nabla}\phi\cdot d\vec{r}\),

onde introduzimos o operador (vetorial)

\(\displaystyle \vec{\nabla}=\hat{i}\frac{\partial}{\partial x}+ \hat{j}\frac{\partial}{\partial y}+ \hat{k}\frac{\partial}{\partial y}\),

denominado de gradiente. Sua interpretação geométrica é imediata: o valor absoluto da diferencial \(d\phi\) será máximo quando o gradiente \(\vec{\nabla}\phi\) estiver alinhado com o deslocamento infinitesimal \(d\vec{r}\). O gradiente aponta a direção de maior crescimento.

Divergente. O divergente é o limite de fluxo por unidade de volume,

\(\displaystyle \text{div}\,\vec{E}=\lim\limits_{V\to 0}\frac{1}{V} \int\limits_{A\supset V}\vec{E}\cdot d\vec{a} =  \vec{\nabla}\cdot\vec{E}\).

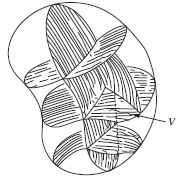
A última igualdade estabelece a sua forma operacional. A Figura da esquerda mostra uma volume finito subdividido em um número infinito de volumes infinitesimais \(V\) (envolta pela área \(A\)). A soma de todos os fluxos nestes volumes infinitesimais, por unidade de volume, é a divergência do campo vetorial \(\vec{E}\). Note que o divergente resulta em um campo escalar.

Rotacional. O rotacional é circulação por unidade de área,

\(\displaystyle \text{rot}\,\vec{E}=\lim\limits_{A\to 0}\frac{1}{A} \int\limits_{C\supset A}\vec{E}\cdot d\vec{r}\;\hat{n}= \vec{\nabla}\times\vec{E}\).

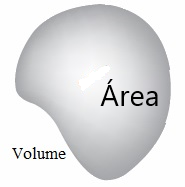
A última igualdade estabelece a sua forma operacional. A Figura da direita mostra uma área finita subdividida em um número infinito de áreas infinitesimais \(A\) (envolta pela curva \(C\)). A soma de todos as circulações nestas curvas infinitesimais, por unidade de área, é o rotacional do campo vetorial \(\vec{E}\). Note que o rotacional resulta em um campo vetorial.

Tab.: Fluxos e circulações

Volumes	Áreas

Fluxo: \(\displaystyle \Phi=\int\limits_{A\supset V}\vec{E}\cdot d\vec{a}\), onde \(d\vec{a}\) está na direção perpendicular ao elemento de área \(da\) e a área \(A\) é o bordo do volume \(V\).

Circulação: \(\displaystyle \int\limits_{C\supset A}\vec{E}\cdot d\vec{r}\), onde \(d\vec{r}\) é o deslocamento tangente à curva \(C\), bordo da área \(A\).

Tab.: Teoremas

Gradiente	Rotacional	Divergente
\(\displaystyle\int\limits_{P=\partial C}d\phi = \int\limits_{C}\vec{\nabla}\phi\cdot d\vec{r}\)	\(\displaystyle\int\limits_{C=\partial A}\vec{E}\cdot d\vec{r} =\int\limits_{A}\vec{\nabla}\times\vec{E}\cdot d\vec{a}\)	\(\displaystyle\int\limits_{A=\partial V}\vec{E}\cdot d\vec{a} =\int\limits_{V}\vec{\nabla}\cdot\vec{E}\, dV\)