Programação
-
Aula 10
Regressão Linear com transformação de variáveis
(clique aqui para acessar a Google Meet desta aula)
-
Agenda
-
Síntese: Vimos na aula passada, quando explorávamos os dados de longevidade, IDH e PIB per capta de 182 países, que a relação PIB per capta se relacionava com IDH, mas que essa relação não era linear. Veremos que, nesse caso, uma simples transformação matemática da variável PIB per capta torna a sua relação com IDH mais linear, sendo possível, portanto, propor uma análise de regressão linear convencional. Faremos isso na primeira parte da aula e, em seguida, divididos em grupos, analisaremos um outro problema para melhor assimilação dessa técnica de transformação de variáveis.
- Dinâmica: Apresentaremos um novo problema e um conjunto de regras que nos ajudarão a escolher o tipo de transformação de variáveis que melhor se aplica, para que as técnicas de regressão linear que estamos aprendendo tenha a sua aplicabilidade estendida.
-
Síntese: Vimos na aula passada, quando explorávamos os dados de longevidade, IDH e PIB per capta de 182 países, que a relação PIB per capta se relacionava com IDH, mas que essa relação não era linear. Veremos que, nesse caso, uma simples transformação matemática da variável PIB per capta torna a sua relação com IDH mais linear, sendo possível, portanto, propor uma análise de regressão linear convencional. Faremos isso na primeira parte da aula e, em seguida, divididos em grupos, analisaremos um outro problema para melhor assimilação dessa técnica de transformação de variáveis.
-
Ajustando a linearidade da relação PIB per capta vs IDH estudada na aula passada
Vamos retomar os dados de 182 países apresentados na aula passada. Exploramos a hipótese de PIB per capta ser positivamente correlacionado com índice de desenvolvimento humano (IDH), isto é, quanto maior o PIB maior seria o IDH. Vimos que essas duas variáveis tem correlação positiva, entretanto, notamos que a relação não apresentava linear.
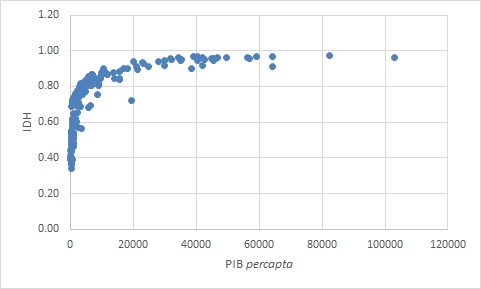
Acompanhe a proposta de transformação da variável PIB per capta apresentada pelo professor em sala de aula, e veja as consequências sobre a hipótese de linearidade.
-
Transformação de variáveis para adequação da análise de regressão linear
Durante a fase exploratória de dados, é comum encontrarmos uma relação aparentemente não linear entre duas variáveis. Métodos específicos para o ajuste de relações não lineares existem, mas estão fora do escopo deste curso. Entretanto, em alguns casos, uma simples transformação matemática numa das variáveis (dependente ou independente), ou nas duas, torna a relação mais linear e viáveis os métodos de regressão estudados até agora. Vejamos o seguinte problema.
Uma empresa que oferece serviços de asfaltamento para prefeituras observa a seguinte relação entre tamanho da equipe e área asfaltada. Essa empresa está no mercado há vários anos e utiliza técnicas convencionais de asfaltamento. Um novo composto fabricado com borracha extraída de pneus reciclados será oferecido a seus clientes. A empresa precisa de estimativas de custo de asfaltamento para esse composto e resolve analisar, com base em experiência prévia, a relação “área asfaltada” x “equipes de trabalho”. Uma análise preliminar e exploratória de 150 ordens de serviço anteriores está disponível para essa análise.
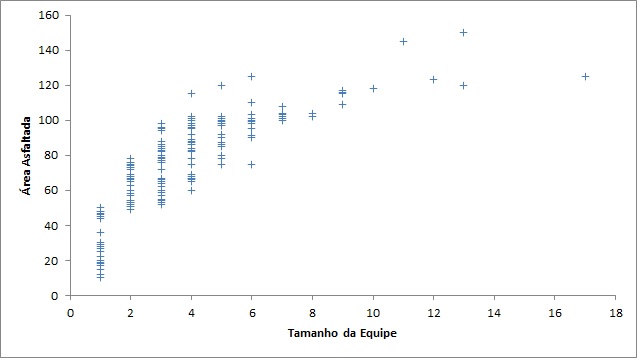
Faremos as seguintes pressuposições (usuais quando usamos métodos de regressão linear simples):
- A relação entre a variável dependente y e a variável independente x é linear (y = β0 + β1 x + ε) com valor esperado do erro igual a 0, ou seja, E(εi)=0 para todo i.
- Todos os erros têm a mesma variância, ou seja, Var(εi) = σ2 para todo
- Os erros são independentes entre si.
- Os erros são normalmente distribuídos, ou seja, εi é normalmente distribuído para todo
Ao observarmos o gráfico, vemos que o aumento do tamanho da equipe, apesar do aumento na área asfaltada, não é linear. De fato, a partir de um certo tamanho, o aumento da equipe parece não levar a aumentos de área asfaltada expressivos. A taxa de crescimento da área asfaltada por jornada de trabalho conforme aumentamos a equipe parece ser decrescente.
Nesse tipo de situação, avaliamos se a transformação das variáveis do problema pode ser recomendada dando os seguintes passos:
- Se a análise exploratória dos dados indica uma relação crescente a taxas decrescentes, e se a variabilidade em torno da estimativa for aproximadamente constante, transforme x usando raiz quadrada, logaritmo ou inverso.
- Se a análise indicar uma relação crescente a taxas crescentes, e se a variabilidade em torno da estimativa for aproximadamente constante, considere x e x2 simultaneamente como variáveis explicativas. Como este método envolve duas variáveis, utilize métodos de regressão múltipla.
- Se a análise indicar uma relação crescente até certo máximo com subsequente decréscimo, e se a variabilidade em torno da estimativa for aproximadamente constante, considere também o uso de x e x2 como variáveis explicativas em um único modelo de regressão linear múltipla.
- Se a análise indicar uma relação crescente a taxas decrescentes, e se a variabilidade em torno da estimativa também crescer com o aumento do valor y estimado, experimente o uso de y2 como variável dependente.
- Se a análise indicar uma relação crescente a taxas crescentes com variabilidade em torno da estimativa também crescente conforme y aumenta, experimente o uso de ln(y) como variável dependente. Pode também ser útil às vezes, considerar o logaritmo natural da variável independente, ln(x).
Reúnam-se em grupos nas salas virtuais, façam o download dos dados apresentados no gráfico acima clicando AQUI, terminem de preencher a planilha como já feito em aulas anteriores (segundo o roteiro básico de cálculos para exercícios de regressão linear simples) e discutam qual transformação se mostra mais recomendável. Resumam as suas conclusões para discussão na sala principal.
Sala 1 Sala 2 Sala 3
-