Dinâmica

Lei de Hooke. Por volta de 1660 Hooke descobriu experimentalmente o comportamento da deformação de objetos. Quando deformado, comprimido ou esticado, o objeto tende a se restaurar. Para pequenas deformações, a restauração é proporcional à deformação. Essa é a lei de Hooke. Na mesma época, Newton estava estabelecendo suas leis do movimento, bem como a teoria da gravitação. Hoje podemos parafrasear a lei de Hooke em termos de forças, as mesmas que aparecem na segunda lei: a força restauradora produzida por uma pequena deformação em um objeto é proporcional à deformação e está na mesma direção da deformação. A lei de Hooke permitiu a construção de molas com as mais variadas capacidades restauradoras e formatos. A capacidade de restauração de uma mola é dada pela chamada constante de mola \(k\), determinada experimentalmente.

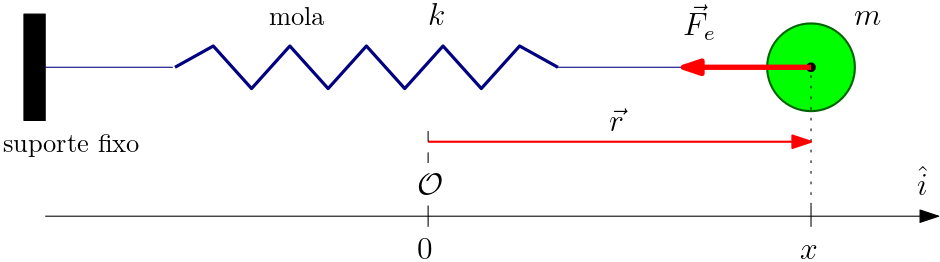
Força elástica. A Figura 1 mostra uma mola de constante $k>0$, em forma de uma espiral. Uma das extremidades está presa no suporte mantido fixo (lado esquerdo). Na outra extremidade da mola há um objeto de massa $m$, o qual é permitido movimentar-se na direção da deformação. Esse sistema mecânico é denominado de massa-mola. O sistema de coordenadas mais adequado está mostrado na Figura 1, onde a deformação está em um dos eixos e a origem $\mathcal{O}$ corresponde a uma deformação nula na mola. Desta forma, a posição $x$ do objeto de massa $m$ também indica a deformação aplicada à mola. Para $x>0$ a mola está esticada (situação indicada na figura). Para $x<0$ a mola está comprimida. Assim a lei de Hooke toma a forma \begin{equation} \vec{F}_{e}=-kx\,\hat{i}. \end{equation} Note esta força elástica é dependente da posição $x$ da massa presa à mola e sempre oposta à deformação ($|x|$) graças ao sinal negativo presente nela (verifique). A constante de mola $k$ é sempre positiva.

Fatos experimentais. A observação cuidadosa do sistema massa-mola exibido na Figura 1, completamente isolado, revela os seguintes fatos.

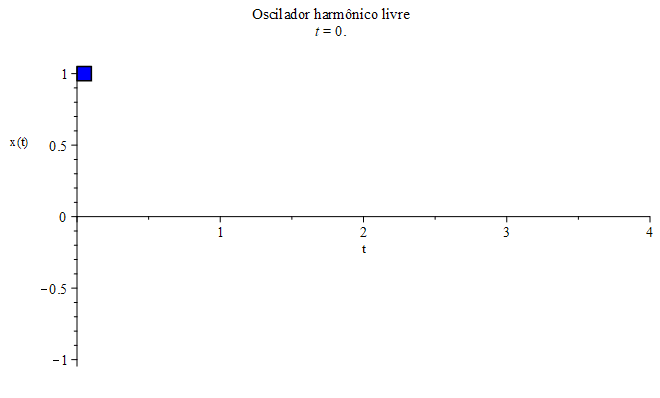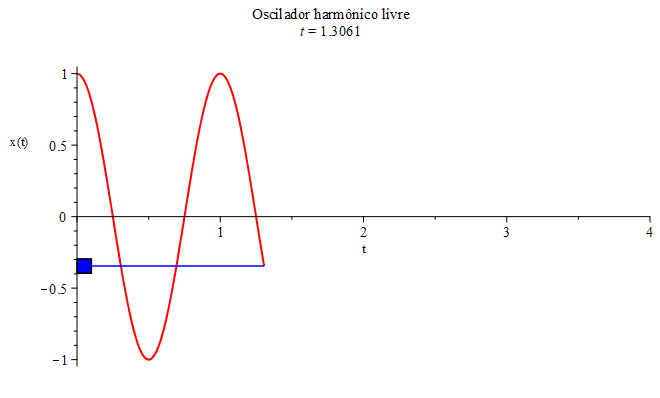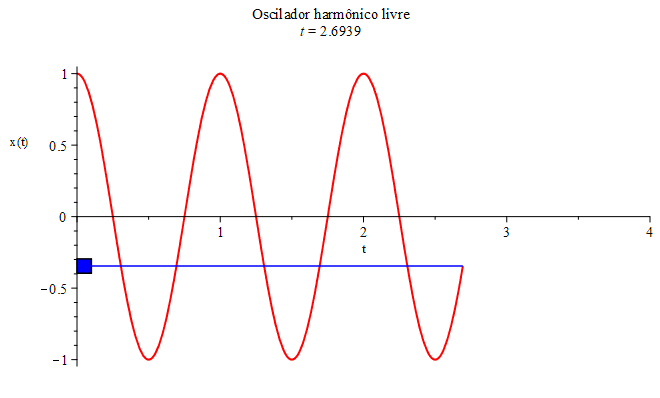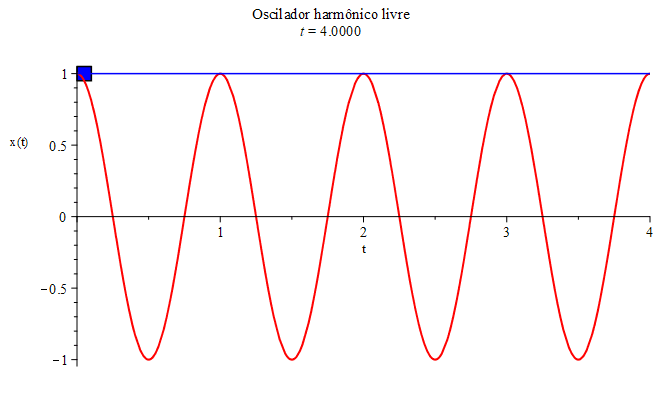
1. A massa $m$ executa um movimento oscilatório, limitado a uma certa região retilínea de comprimento $2A$, como mostrado na Figura 2 (com $A=1$). A quantidade $A$ é denominada de amplitude.
   
2. Esse movimento oscilatório tem uma frequência (fixa) que depende apenas da massa $m$ e da constante de mola $k$. A frequência não depende da amplitude.
3. Na ausência de outras forças, esse movimento oscilatório é permanente, harmônico. Porém, na presença da atmosfera, a qual contribui com uma força viscosa, esse movimento cessa.
   

Segunda lei. A Figura 1 representa a massa sujeita à força elástica $\vec{F}_{e}$ num dado instante de tempo $t$ após o momento inicial $t_{0}$. Neste instante $t$, a massa $m$ encontra-se numa determinada posição especificada pelo vetor posição $\vec{r}$, cuja única componente é $x$ (sabemos que a trajetória será retilínea). Portanto,  os vetores cinemáticos, escritos em coordenadas, no mesmo sistema de coordenadas $\mathcal{O}$ em que a força elástica foi escrita, são \begin{equation} \vec{r}=x\,\hat{i},\; \vec{v}=\dot{x}\,\hat{i},\; \vec{a}=\ddot{x}\,\hat{i}. \end{equation} desta forma, a segunda lei $\vec{F}_{e}=\dot{\vec{p}}=m\vec{a}$ (massa constante), fornece a seguinte EDO (verifique): \begin{equation} -kx=m\ddot{x} \implies \ddot{x}=-\omega_{0}^{2}\,x,\; \omega_{0}=\sqrt{\frac{k}{m}}.\end{equation} Note que a constante (ou parâmetro) $\omega_{0}$ tem dimensões de frequência (inverso do tempo; verifique), \begin{equation} [k]=\frac{M}{T^{2}},\quad [\omega_{0}]=\frac{1}{T}.\end{equation}

Equação horária. Essa EDO está nos perguntando se conhecemos "uma função cuja derivada segunda é proporcional a ela mesma". Note que essa constante de proporcionalidade é estritamente negativa, $-\omega_{0}^{2}$. Sim, conhecemos as funções trigonométricas (seno e cosseno). Assim, a equação horária pode ser da forma \begin{equation} x(t)=A\cos\theta(t), \end{equation} com $A$ constante e $\theta(t)$ uma função ainda desconhecida do tempo. Lembre-se que o cosseno é uma função transcendental e, como tal, seu argumento deve ser adimensional. Portanto, $[A]=[x]=L$. Tomemos a derivada segunda (verifique) dessa equação horária (proposta de solução), sem esquecer que as funções trigonométricas são funções compostas, \begin{equation} \dot{x}=-A\dot{\theta}\sin\theta,\quad \ddot{x}=-A\,\dot{\theta}^{2}\cos\theta-A\,\ddot{\theta}\sin\theta.\end{equation} Momento de substituir (verifique) a derivada segunda na EDO, \begin{equation} \ddot{x}=-\omega_{0}^{2}\,x \implies \dot{\theta}^{2}\cos\theta+\ddot{\theta}\sin\theta=\omega_{0}^{2}\cos\theta.\end{equation} Este resultado pode ser reescrito numa forma mais organizada, coletando os termos em cosseno e seno, (verifique) \begin{equation} (\dot{\theta}^{2}-\omega_{0}^{2})\cos\theta+\ddot{\theta}A\sin\theta=0.\end{equation} A trigonometria nos ensinou que uma função trigonométrica não pode ser escrita como múltipla da outra, ou seja, as funções cosseno e seno são linearmente independentes, \begin{equation} a\cos\theta+b\sin\theta=0 \implies a=b=0.\end{equation} A expressão que obtivemos anteriormente, decorrente da substituição da equação horária proposta na EDO do sistema massa-mola, é justamente uma combinação linear de duas funções linearmente independentes. Portanto, cada coeficiente nesta equação deve ser nulo (única solução possível), \begin{equation} \dot{\theta}^{2}-\omega_{0}^{2}=0,\quad \ddot{\theta}=0.\end{equation} A última dessas duas EDOs para a função $\theta(t)$, denominada de fase (argumento de uma função trigonométrica), implica que ela seja uma função linear do tempo (verifique), \begin{equation} \ddot{\theta}=0 \implies \theta(t)=\varphi+\omega t \implies \dot{\theta}=\omega,\end{equation} com $\varphi$ e $\omega$ constantes. Substituindo esse resultado na outra EDO para $\theta$, encontramos (verifique) o valor da constante $\omega$, \begin{equation} \dot{\theta}^{2}-\omega_{0}^{2}=0 \implies \dot{\theta}^{2}=\omega^{2}\omega_{0}^{2} \implies \omega=\pm \omega_{0}.\end{equation} Como as funções trigonométricas possuem paridades bem definidas (o cosseno é uma função par e o seno é uma função ímpar) e $A$ e $\varphi$ são arbitrárias (o que significa que podemos reescrevê-las como $-A$ e $-\varphi$), podemos ignorar (verifique) o sinal o negativo em $\omega=\pm \omega_{0}$. Assim, a equação horária $x(t)$, solução da EDO do sistema massa-mola, é \begin{equation}\ddot{x}=-\omega_{0}^{2}\,x \implies x(t)=A\cos\theta(t),\; \theta(t)=\varphi+\omega_{0} t.\end{equation} Por razões óbvias, a constante $A$ é denominada de amplitude, $\varphi$ de constante da fase e $\omega_{0}$ de frequência (angular) natural. Essa EDO do sistema massa-mola aparece em muitos outros modelos em diversas áreas do conhecimento. Ela deve ser memorizada.

Condições iniciais. As duas constantes $A$ (amplitude) e $\varphi$ (constante da fase) devem ser determinadas pelas condições iniciais. Por exemplo, suponha que no instante inicial $t_{0}=0$ a massa $m$ seja solta do repouso, portanto com velocidade inicial nula, $\dot{x}(0)=0$, na posição $x(0)=1$ (uma unidade de comprimento). Impondo que a velocidade inicial seja nula (repouso), determinamos a constante da fase, \begin{equation}\dot{x}(0)=-\omega_{0}A\sin\varphi=0\implies \varphi=0. \end{equation} Com a constante da fase determinada, $\varphi=0$, a posição inicial determina a amplitude, \begin{equation}x(0)=A\cos(0)=1\implies A=1.\end{equation} Escolhendo $\omega_{0}=1$ (inverso da unidade de tempo), a equação horária correspondente a este exemplo, $x(t)=cos(t)$ (em unidades de comprimento), está mostrada na Figura 2, juntamente com o movimento da massa $m$ em sua trajetória retilínea e oscilatória (na vertical, por comodidade). Esse sistema massa-mola também é conhecido por oscilador harmônico. O adjetivo harmônico vem da presença de uma função trigonométrica elementar (periódica) na equação horária.

Modelagem. Naturalmente, a concordância entre a previsão feita pelo modelo matemático para a frequência de oscilação,\begin{equation} f=2\pi\omega_{0},\; \omega_{0}=\sqrt{\frac{k}{m}},\end{equation} e o valor medido experimentalmente é excelente, perfeita. Note o fator $2\pi$ na frequência que é medida no laboratório. A inclusão de uma força viscosa, produzida por um fluido, como a atmosfera ou óleo no caso de amortecedores, leva à indústria bilionário dos amortecedores.

Exercícios. Detalhe todas as passagens sinalizadas por "verifique".